统计学常用知识-Pearson相关系数-显著检验-置信区间
有多种相关系数,此处介绍Pearson相关系数;以及显著检验
协方差
要理解 Pearson 相关系数,首先要理解协方差(Covariance)。方差大家可能比较熟悉,方差表示某个变量偏离均值的波动情况;而协方差表示的是两个变量 X,Y 的相互关系,其计算公式为:
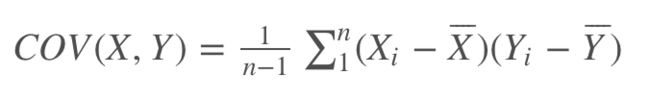
X=Y时,协方差即方差。可以想象,X 和 Y如果变化趋势一致时,则COV(X,Y)>0,变化趋势相反时,COV(X,Y)<0。具体例子可以看下面图形示例。
由此可以利用协方差来衡量X Y的相关情况。
Pearson相关系数
Pearson相关系数(通常也称为R值)即延伸自上述协方差公式。具体公式如下:

可以看出 Pearson 相关系数是用协方差除以两个变量的标准差得到的。
虽然协方差能反映两个随机变量的相关程度(协方差大于0的时候表示两者正相关,小于0的时候表示两者负相关),但其绝对数值受量纲影响很大。比如X扩大10倍,COV(X,Y)增加10倍,但是X/Y的相关性并没有实质变化。
为了消除这种量纲的影响,就再除以两个变量的标准差,做标准化,就能得到稳定可比较的相关系数。相关系数例子如下图:
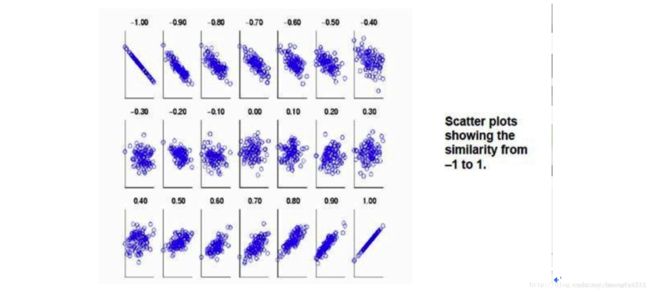
相关系数的计算显然要求X Y的方差都不为0。相关系数的取值范围为[-1,1]。
值得注意的是,R值衡量的是X Y的线性相关情况,该值趋向于0时,只能说明X Y线性相关性越来越弱。但是X Y可能存在很强的非线性相关,如 X2+Y2=1。
R=-1,表明X Y 负相关,相关程度很强;
显著检验
【为什么】:因为相关系数通常是根据样本数据计算出来的,而样本一般是随机的,所以相关系数是一个随机变量,其取值具有一定的偶然性。
两个不相关的变量,根据样本计算的相关系数也可能较高,这在统计上称为虚假相关。要从样本相关系数判断总体中是否也有这样的关系,则需要对相关系数进行统计检验后才能得出结论。
【是什么】:下面是理论,比较抽象,可直接看怎么做部分;显著性检验(significance test)就是事先对总体(随机变量)的参数或总体分布形式做出一个假设,然后利用样本信息来判断这个假设(备择假设)是否合理,即判断总体的真实情况与原假设是否有显著性差异。或者说,显著性检验要判断样本与我们对总体所做的假设之间的差异是纯属机会变异,还是由我们所做的假设与总体真实情况之间不一致所引起的。 显著性检验是针对我们对总体所做的假设做检验,其原理就是“小概率事件实际不可能性原理”来接受或否定假设(参考资料相关性和显著性检验学习笔记)。
常把一个要检验的假设记作H0,称为原假设(或零假设) (null hypothesis) ,与H0对立的假设记作H1,称为备择假设(alternative hypothesis) 。
⑴ 在原假设为真时,决定放弃原假设,称为第一类错误,其出现的概率通常记作α;
⑵ 在原假设不真时,决定不放弃原假设,称为第二类错误,其出现的概率通常记作β
(3)α+β 不一定等于1 。
通常只限定犯第一类错误的最大概率α, 不考虑犯第二类错误的概率β。这样的假设检验 又称为显著性检验,概率α称为显著性水平。
最常用的α值为0.01、0.05、0.10等。一般情况下,根据研究的问题,如果放弃真假设损失大,为减少这类错误,α取值小些 ,反之,α取值大些。
显著系数p:p值即概率,反映某一事件发生的可能性大小。统计学根据显著性检验方法所得到的p 值,一般以p < 0.05 为有统计学差异,p<0.01 为有显著统计学差异,p<0.001为有极其显著的统计学差异。
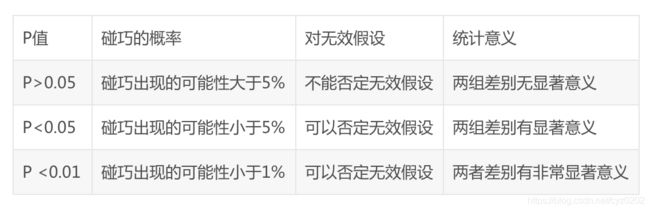
【怎么做】:推荐知乎-马同学的一篇回答,写的很好
简要说一下,以扔硬币为例。路人甲街头卖艺,拿了一枚一般人看不出来的假硬币,他声称硬币是正常公平的,游客扔10次,只要超过5次为 字,就能得到100块,反之要给路人甲50块。
那马同学看路人甲这么自信,不相信硬币是公平的,所以说要扔10000次来检验,如果花明显容易出现,那硬币就有假。
这就是假设检验:
- 假设硬币是公平的(原假设,备择假设为硬币不公平)
- 马同学要检验这个假设:扔10000次,看实验的结果是不是和假设相符;为了方便说明,还是假设扔10次吧
需要提一下原假设附加的显著性水平 α \alpha α,一般设为0.05,用于表示拒绝原假设的概率范围;即 如果观测到的样本 对应的概率(p-value)小于该 α \alpha α,那么认为在原假设成立的情况下 居然 发生了 小概率事件,所以拒绝原假设成立;
再提一下p-value(p值),一般表示观测数据在原假设条件下的 出现概率;p-value的计算 会根据 不同的检验方法 采用不同的方式;但是只要小于 α \alpha α,那就拒绝原假设;
p-value作为一种方法,可以应用于任何假设检验:只要小于给定的显著水平,那么就拒绝原假设。好比p-value是一杆秤,不同的检验方法就如同不同的猪肉鸭肉牛肉,你想买一斤肉,那么称出来也必须是一斤。不同的XX检验对应的统计量(test statistics)不一样,已知方差的正态均值就是Z检验,未知方差的(正态或大样本)均值就是t检验等等。卡方检验可以用在很多地方,不太方便归类,换句话说,很多不同的假设检验最后都可以归结到卡方检验上(最常见的就是分布拟合检验等等),但其因为卡方本身是非负的,所以一般只考虑单尾,即右边的那个尾部概率。(来自知乎-Yeung Evan)
回到例子,在原假设成立的情况下,反复扔硬币符合二项分布:
X ∽ B ( n , μ ) X \backsim B(n, \mu) X∽B(n,μ)
其中n代表扔的次数, μ \mu μ代表花 朝上的概率,即0.5,对于10次试验
X ∽ B ( 10 , 0.5 ) X \backsim B(10, 0.5) X∽B(10,0.5)
马同学扔了10次,8次花。。。一位数学大佬定义了p-value(P值),即极端值相加的概率,同时分为单侧p值和双侧p值;对于8次花,单侧p-value为
p − v a l u e = P ( 8 ≤ X ≤ 10 ) = 0.05 p-value=P(8 \leq X \leq 10)=0.05 p−value=P(8≤X≤10)=0.05
如下图所示
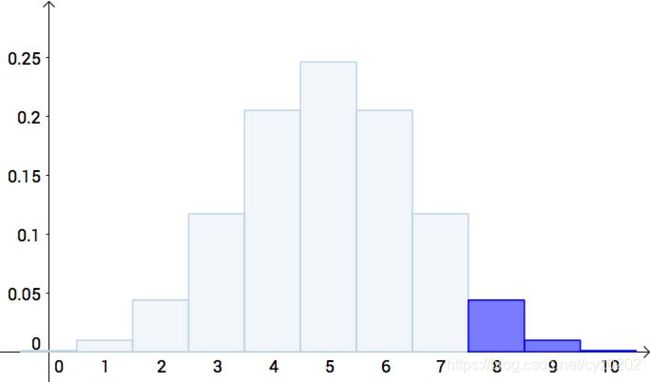
其实,出现两次正面、一次正面、零次正面的概率也是很极端的
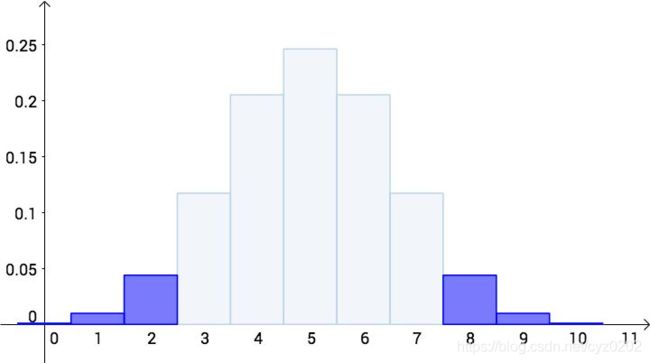
所以双侧p-value
p − v a l u e = P ( 0 ≤ X ≤ 2 ) + P ( 8 ≤ X ≤ 10 ) = 0.1 p-value=P(0 \leq X \leq 2) + P(8 \leq X \leq 10)=0.1 p−value=P(0≤X≤2)+P(8≤X≤10)=0.1
之所以考虑把8次及以上的极端值加起来,马同学说 应该是考虑连续变量的情况下用正态分布计算比较简单,而且连续变量并没有单点概率
如果只考虑单侧p-value,显然在原假设成立条件下,出现8次花的p-value
p − v a l u e = P ( 8 ≤ X ≤ 10 ) = 0.05 ≤ 0.05 p-value=P(8 \leq X \leq 10)=0.05 \leq 0.05 p−value=P(8≤X≤10)=0.05≤0.05
和原假设的显著水平一样,可以拒绝原假设,只是没有那么“显著”;可以想象如果出现9次花(此时p-value=0.01),则完全拒绝原假设,即硬币不公平;附图

Z检验
待更新
T检验
待更新
对于相关系数的假设检验会麻烦一点,但思路是一样的:判断在原假设成立条件下,观察到的数据的p-value与显著水平 α \alpha α的关系 来接受或者拒绝原假设;有时间再更新
置信区间
顺便介绍一下置信区间,同样推荐 马同学的回答(然鹅马同学并不知道我这么认真给他推荐啊)
简要说一下,置信区间的目的是为了避开 点估计的不确定性,通过区间估计来更准确地表述一个事实
比如 你说 我随便抓一个20岁的男生过来,他身高1.75m,那路人甲肯定不怎么相信,虽然1.75m是比较可能的身高;
那么这时你如果说,这个20岁的男生的身高,95%的概率被[1.65m,1.85m]包含,那路人甲乙丙丁就很相信了。
关键是怎么计算95%的置信区间。下面介绍一个常见套路。
常见的例子是求身高均值u的95%置信区间。真实的u一般不知道,可以通过样本的平均值 u ˉ \bar{u} uˉ估计。假设身高h 服从均值为u,方差为 θ \theta θ的高斯分布
h ∽ N ( u , θ 2 ) h \backsim N(u,\theta^2) h∽N(u,θ2)
u未知,而 θ \theta θ简单起见可以假设是已知的。采样n个数据点(n个20岁男生的身高),则
u ˉ = h 1 + h 2 + . . . + h n n \bar{u} = \frac {h1+h2+...+hn} {n} uˉ=nh1+h2+...+hn
根据大数定律和中心极限定理, u ˉ \bar{u} uˉ服从
u ˉ ∽ N ( u , θ 2 n ) \bar{u} \backsim N(u, \frac {\theta^2}{n}) uˉ∽N(u,nθ2)
根据正态分布的特点,可以求出 u ˉ \bar{u} uˉ的95%区间为
P ( u − 1.96 θ n ≤ u ˉ ≤ u + 1.96 θ n ) P(u-1.96 \frac{\theta}{\sqrt{n}} \leq \bar{u} \leq u+1.96 \frac{\theta}{\sqrt{n}}) P(u−1.96nθ≤uˉ≤u+1.96nθ)
也即,
P ( u ˉ − 1.96 θ n ≤ u ≤ u ˉ + 1.96 θ n ) P(\bar{u}-1.96 \frac{\theta}{\sqrt{n}} \leq u \leq \bar{u}+1.96 \frac{\theta}{\sqrt{n}}) P(uˉ−1.96nθ≤u≤uˉ+1.96nθ)
这就是u 通过样本计算的一个95%置信区间
那么假设检验与置信区间有什么关系
按照马同学的说法,如果我们提出来的假设 [公式] 在样本 [公式] 的置信区间内,就可以通过测试,附马同学的图两张(检验通过与检验不通过, x ˉ \bar{x} xˉ可视为样本均值)

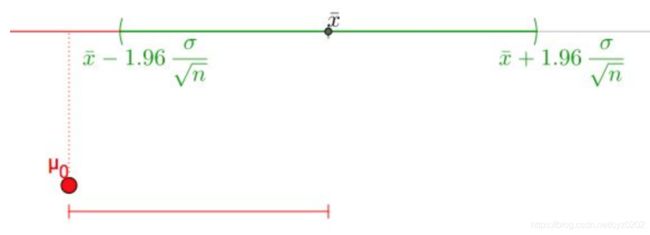
P.S 以上是我的一些理解和总结,欢迎大佬指正^^