图 | 存储结构:邻接表、邻接多重表、十字链表及C语言实现
上一节介绍了如何使用顺序存储结构存储图,而在实际应用中最常用的是本节所介绍的链式存储结构:图中每个顶点作为链表中的结点,结点的构成分为数据域和指针域,数据域存储图中各顶点中存储的数据,而指针域负责表示顶点之间的关联。
使用链式存储结构表示图的常用方法有 3 种:邻接表、邻接多重表和十字链表。
邻接的意思是顶点之间有边或者弧存在,通过当前顶点,可以直接找到下一个顶点。
邻接表
使用邻接表存储图时,对于图中的每一个顶点和它相关的邻接点,都存储到一个链表中。每个链表都配有头结点,头结点的数据域不为NULL,而是用于存储顶点本身的数据;后续链表中的各个结点存储的是当前顶点的所有邻接点。
所以,采用邻接表存储图时,有多少顶点就会构建多少个链表,为了便于管理这些链表,常用的方法是将所有链表的链表头按照一定的顺序存储在一个数组中(也可以用链表串起来)。
总结起来,邻接表的处理方法是这样:
- 图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,不过数组可以较容易地读取顶点信息,更加方便。
- 图中每个顶点 Vi 的所有邻接点构成一个线性表,由于邻接点的个数不确定,所以我们选择用单链表来存储。
在邻接表中,每个链表的头结点和其它结点的组成成分有略微的不同。各自的结构构成如下图所示:

表头结点结构:
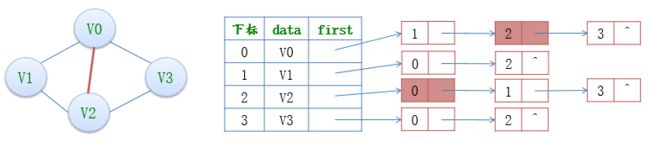
data域存储该顶点含有的数据;firstarc为指针域,指向当前顶点的首个邻接点。
其他节点结构:
adjvex存储邻接点在数组中的位置下标;nextarc指向下一个结点(邻接点)的指针;info记录权值的信息域。
info 域对于无向图来说,本身不具备权值和其它相关信息,就可以根据需要将之删除。
例如,当存储图 2(A)所示的有向图时,构建的邻接表如图 2(B)所示:
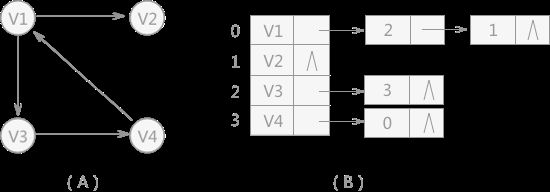
邻接表存储图的存储结构为:
#define MAX_VERTEX_NUM 20 //最大顶点个数
#define VertexType int //顶点数据的类型
#define InfoType int //图中弧或者边包含的信息的类型
typedef struct ArcNode{
int adjvex; //邻接点在数组中的位置下标
struct ArcNode * nextarc;//指向下一个邻接点的指针
InfoType * info; //信息域
}ArcNode;
typedef struct VNode{
VertexType data; //顶点的数据域
ArcNode * firstarc; //指向邻接点的指针
}VNode,AdjList[MAX_VERTEX_NUM];//存储各链表头结点的数组
typedef struct {
AdjList vertices; //图中顶点及各邻接点数组
int vexnum,arcnum; //记录图中顶点数和边或弧数
int kind; //记录图的种类
}ALGraph;
邻接表计算顶点的度
使用邻接表存储无向图时,各顶点的度为各自链表中包含的结点数;存储有向图时,各自链表中具备的结点数为该顶点的出度。求入度时,需要遍历整个邻接表中的结点,统计数据域和该顶点数据域相同的结点的个数,即为顶点的入度。
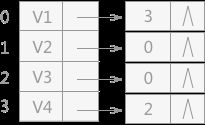
对于求有向图中某结点的入度,还有一种方法就是再建立一个逆邻接表,此表只用于存储图中每个指向该顶点的所有的顶点在数组中的位置下标。例如,构建图 2(A)的逆邻接表,结果为:
对于具有 n 个顶点和 e 条边的无向图,邻接表中需要存储 n 个头结点和 2e 个表结点。在图中边或者弧稀疏的时候,使用邻接表要比前一节介绍的邻接矩阵更加节省空间。
十字链表
十字链表存储的对象是有向图或者有向网。同邻接表相同的是,图(网)中每个顶点各自构成一个链表,为链表的首元结点。同时,对于有向图(网)中的弧来说,有弧头和弧尾。一个顶点所有的弧头的数量即为该顶点的入度,弧尾的数量即为该顶点的出度。每个顶点构成的链表中,以该顶点作为弧头的弧单独构成一个链表,以该顶点作为弧尾的弧也单独构成一个链表,两个链表的表头都为该顶点构成的头结点。
这样,由每个顶点构建的链表按照一定的顺序存储在数组中,就构成了十字链表。
所以,十字链表中由两种结点构成:顶点结点和弧结点。各自的结构构成如下图所示:

弧结点结构:
tailvex和headvex分别存储的是弧尾和弧头对应的顶点在数组中的位置下标;hlink和tlink为指针域,分别指向弧头相同的下一个弧和弧尾相同的下一个弧;info为指针域,存储的是该弧具有的相关信息,例如权值等。
顶点结点结构(图中顶点也是用一个一维数组存储,只是为了方便画线没有连在一起):
data域存储该顶点含有的数据;firstin和firstout为两个指针域,分别指向以该顶点为弧头和弧尾的首个弧结点。
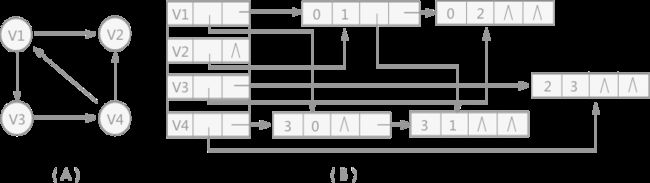
例如,使用十字链表存储有向图 5(A) ,构建的十字链表如图 (B) 所示,构建代码实现为:
#define MAX_VERTEX_NUM 20
#define InfoType int //图中弧包含信息的数据类型
#define VertexType int
typedef struct ArcBox{
int tailvex,headvex; //弧尾、弧头对应顶点在数组中的位置下标
struct ArcBox *hlik,*tlink;//分别指向弧头相同和弧尾相同的下一个弧
InfoType *info; //存储弧相关信息的指针
}ArcBox;
typedef struct VexNode{
VertexType data; //顶点的数据域
ArcBox *firstin,*firstout;//指向以该顶点为弧头和弧尾的链表首个结点
}VexNode;
typedef struct {
VexNode xlist[MAX_VERTEX_NUM];//存储顶点的一维数组
int vexnum,arcnum; //记录图的顶点数和弧数
}OLGraph;
int LocateVex(OLGraph * G,VertexType v){
int i=0;
//遍历一维数组,找到变量v
for (; i<G->vexnum; i++) {
if (G->xlist[i].data==v) {
break;
}
}
//如果找不到,输出提示语句,返回 -1
if (i>G->vexnum) {
printf("no such vertex.\n");
return -1;
}
return i;
}
//构建十字链表函数
void CreateDG(OLGraph *G){
//输入有向图的顶点数和弧数
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
//使用一维数组存储顶点数据,初始化指针域为NULL
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->xlist[i].data));
G->xlist[i].firstin=NULL;
G->xlist[i].firstout=NULL;
}
//构建十字链表
for (int k=0;k<G->arcnum; k++) {
int v1,v2;
scanf("%d,%d",&v1,&v2);
//确定v1、v2在数组中的位置下标
int i=LocateVex(G, v1);
int j=LocateVex(G, v2);
//建立弧的结点
ArcBox * p=(ArcBox*)malloc(sizeof(ArcBox));
p->tailvex=i; //存储弧尾对应的顶点在数组中的位置下标
p->headvex=j; //存储弧头对应的顶点在数组中的位置下标
//采用头插法插入新的p结点
p->hlik=G->xlist[j].firstin;//指向弧头相同的下一个弧;
p->tlink=G->xlist[i].firstout;//指向弧尾相同的下一个弧;
G->xlist[j].firstin=G->xlist[i].firstout=p;
}
}
对于链表中的各个结点来说,由于表示的都是该顶点的出度或者入度,所以结点之间没有先后次序之分,程序中构建链表对于每个新初始化的结点采用头插法进行插入。
头插法: 在链表的开头插入一个新的节点,也就是,必须使得链表头Head指向新节点,该新节点指向原来是表头的第一个节点Node newNode; //生成新节点newNode Node curr = head.next; newNode.next = curr; //新节点指向原来的第一节点 head.next = newNode; //头节点指向新节点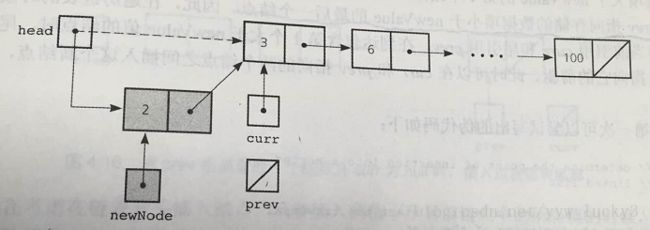
十字链表计算顶点的度
采用十字链表表示的有向图,在计算某顶点的出度时,为 firstout 域链表中结点的个数;入度为 firstin 域链表中结点的个数。
邻接多重表
使用邻接表解决在无向图中删除某两个结点之间的边的操作时,由于表示边的结点分别处在两个顶点为头结点的链表中,所以需要都找到并删除,操作比较麻烦。处理类似这种操作,使用邻接多重表会更合适。
例如,若要删除(V0,V2)这条边,就需要对邻接表结构中边表的两个结点进行删除操作。
邻接多重表可以看做是邻接表和十字链表的结合体。和十字链表唯一不同的是顶点结点和表结点的结构组成不同;同邻接表相比,不同的地方在于邻接表表示无向图中每个边都用两个结点,分别在两个不同链表中;而邻接多重表表示无向图中的每个边只用一个结点。
邻接多重表的顶点结点和表结点的构成如图 6 所示:

表结点构成:
mark为标志域,作用是标记某结点是否已经被操作过,例如在遍历各结点时, mark 域为 0 表示还未遍历;mark 域为 1 表示该结点遍历过;ivex和jvex分别表示该结点表示的边两端的顶点在数组中的位置下标;ilink指向下一条与 ivex 相关的边(或依附顶点 ivex 的下一条边);jlink指向下一条与 jvex 相关的边(或依附顶点 jvex 的下一条边);info指向与该边相关的信息。
顶点结点构成:
data为该顶点的数据域;firstedge为指向第一条跟该顶点有关系的边。
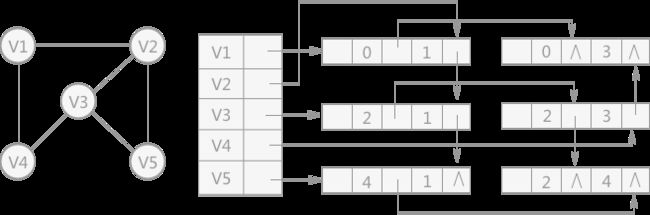
例如,使用邻接多重表表示图 7中左边的无向图时,与之相对应的邻接多重表如图右侧所示。
邻接多重表的存储结构用代码表示为:
#define MAX_VERTEX_NUM 20 //图中顶点的最大个数
#define InfoType int //边含有的信息域的数据类型
#define VertexType int //图顶点的数据类型
typedef enum {
unvisited,visited}VisitIf; //边标志域
typedef struct EBox{
VisitIf mark; //标志域
int ivex,jvex; //边两边顶点在数组中的位置下标
struct EBox * ilink,*jlink; //分别指向与ivex、jvex相关的下一个边
InfoType *info; //边包含的其它的信息域的指针
}EBox;
typedef struct VexBox{
VertexType data; //顶点数据域
EBox * firstedge; //顶点相关的第一条边的指针域
}VexBox;
typedef struct {
VexBox adjmulist[MAX_VERTEX_NUM]; //存储图中顶点的数组
int vexnum,degenum; //记录途中顶点个数和边个数的变量
}AMLGraph;
总结
本节介绍了有关图的三种链式存储结构:邻接表、十字链表和邻接多重表。
邻接表适用于所有的图结构,无论是有向图(网)还是无向图(网),存储结构较为简单,但是在存储一些问题时,例如计算某顶点的度,需要通过遍历的方式自己求得。
十字链表适用于有向图(网)的存储,使用该方式存储的有向图,可以很容易计算出顶点的出度和入度,只需要知道对应链表中的结点个数即可。
邻接多重表适用于无向图(网)的存储,该方式避免了使用邻接表存储无向图时出现的存储空间浪费的现象,同时相比邻接表存储无向图,更方便了某些边操作(遍历、删除等)的实现。