信息安全 - 密码学 （中法）

密码（Cryptographie） 这一节内容较多，是法国老师教的重点。于是为了整理，选取了课件中一些关键点，借助网络，整理如下：

密码学

一、介绍

关键字：隐藏，书写。

定义：密码学是研究编制密码和破译密码的技术科学。

隐写术（Stéganographie）：一门关于信息隐藏的技巧与科学，讲一条信息隐藏在另一条信息中，表面上看起来是A，其实隐藏着信息B。

术语（Terminologie）：

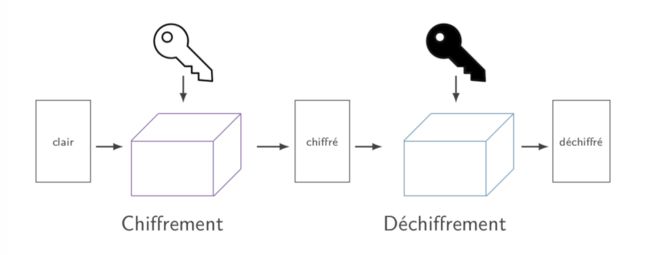
　　Chiffrer / Déchiffrer 
　　Message clair ⇒ Message chiffré (Cryptogramme) Cryptosystème
　　Décrypter
　　Secret : clé

　　密钥：分为加密密钥和解密密钥。

　　明文：没有进行加密，能够直接代表原文含义的信息。

　　密文：经过加密处理处理之后，隐藏原文含义的信息。

　　加密：将明文转换成密文的实施过程。

　　解密：将密文转换成明文的实施过程。

　　密码算法：密码系统采用的加密方法和解密方法，随着基于数学密码技术的发展，加密方法一般称为加密算法，解密方法一般称为解密算法。

 

目的：（主要）保密，完整性，验证；（次要）匿名，隐藏证据等。

历史：

Transmission de messages secrets  　　秘密信息传递

Remonte à l’antiquité 　　可以追溯到古代

Lutte cryptographie/cryptanalyse 　　战争中加密信息及密码分析

Progression lors de conflits　　在冲突中发展

Manuelle - utilise les lettres　　手册：字母的使用

Automatique - utilise des bits Méthodes secrètes　　自动 - 使用秘密位方法

Méthodes publiques à clé secrète　　密钥的公共方法

　 【可以了解一下：中西方古代各有什么加密方法？】 

 

二、主要算法

1. Scytale （转置法）

　　公元前4世纪  加密方法：通过将一条写有字母的带子缠绕在一个柱状物上，横向读。

　　这种方法的密钥是指定直径的柱状物。也就是说，如果直径不同，读出的信息也不同。

　　缺点：机密性不足。

 

2. Chiffre de César 凯撒密码（偏移法，1对1单字母替代）

公元前1世纪 　　

凯撒密码是前者最经典的替代法，据传由古罗马帝国的皇帝凯撒所发明，用在与远方将领的通信上。

每个字母被往后位移n格字母所取代。 n 为偏移值。

密文 =（明文+偏移量n）mod 字母总数

 

  

3. Chiffre de Vigenère 维吉尼亚加密法

 　　公元16世纪晚期，法国外交官维吉尼亚（Vigenere）提出著名的维吉尼亚方阵密表和维吉尼亚密码(Vigenerecypher)，这是一种多表加密的替代密码。Vigenere密码的出现，使得先前对单表置换用的简单频率分析方法失效。

　　ps：这图有点晃瞎眼，但是这些颜色对于看出维吉尼亚字母排序有一定的帮助。

　　人们在单一恺撒密码的基础上扩展出多表密码，多重偏移，多字母替代。

　　维吉尼亚密码引入了“密钥”的概念，即根据密钥来决定用哪一行的密表来进行替换，以此来对抗字频统计。密钥是单词或者句子。

　　方法：Chiffré[i] = (Clair[i] + Clé[i]) mod taille alphabet

　　此法中，收信人和发信人须使用相同的表格和密钥。

假如以上面第一行代表明文字母，左面第一列代表密钥字母，对如下明文加密：

TO BE OR NOT TO BE THAT IS THE QUESTION

当选定 RELATIONS 作为密钥时，加密过程是：明文一个字母为T，第一个密钥字母为R，因此可以找到在 R行中代替T的为K，依此类推，得出对应关系如下：

密钥:RELAT IONSR ELATI ONSRE LATIO NSREL  （密钥relations循环使用）

明文:TOBEO RNOTT OBETH ATIST HEQUE STION

密文:KSMEH ZBBLK SMEMP OGAJX SEJCS FLZSY

　　很多年以来，维吉尼亚（Vigenère）密码都被认为是不可破解的，但一位英国富人巴贝奇（Babbage）通过寻找重复的字母段破解了这个密码系统。关于这段解析，不理解的同学们可以参考 百度百科　　https://baike.baidu.com/item/维吉尼亚密码 

　　公元1863年，普鲁士少校卡西斯基（Kasiski）提出了Kasiski测试法，此方法从密钥的长度着手破解Vigenere密码。思想与巴贝奇相同。

　　

4.  Chiffre de Vernam (1917)  又叫 Masque jetable （一次性密码本）。

一次性密码本（one-time pad，缩写为OTP）是古典密码学中的一种加密算法。是以随机的密钥（key）组成明文，且只使用一次。 

加密方法

首先手上要有一本一次性密码本用以加密文件，接着将一次性密码本里的字母，与被加密文件的字母给依序按某个事先约定的规定一一相混，其中一个相混的作法是将字母指定数字（如在英语中，将A至Z依序指定为0至25）然后将一次性密码文本上的字母所代表的数字和被加密文件上相对应的数字给相加，再除以该语言的字母数后取得其余数，假设字母数是 n（如英语为26），若就此得出来的某个数字小于零，则将该小于零的数给加上n，如此便完成加密。

举个例子，若要加密讯息“This is an example”，而用以加密的一次性密码本如下所示：

MASKL NSFLD FKJPQ

则利用指定数字的方法，可分别将两者给做以下的转换：

• 这是一个例子→19 7 8 18 8 18 0 13 4 23 0 12 15 11 4
• MASKL NSFLD FKJPQ→12 0 18 10 11 13 18 5 11 3 5 10 9 15 16

两者依序相加后得到的讯息如下：

• 31 7 26 28 19 31 18 18 15 26 5 22 24 26 20

将以上得到的讯息模26(除以26后取余数)可得：

• 5 7 0 2 19 5 18 18 11 0 5 22 24 0 20

它也就变成了

• FHACTFSSLAFWYAU

而若要解密以上讯息，反向操作即可。

安全性

在理论上，此种密码具有完善保密性，是牢不可破的。它的安全性已由克劳德·艾尔伍德·香农所证明。

虽然它在理论上的安全性无庸置疑，但在实际操作上却有着以下的问题：

• 用以加密的文本，也就是一次性密码本，必须确实是随机产生的。 aléatoire
• 它至少必须和被加密的文件等长。 au moins aussi longue de le message
• 用以加密的文本只能用一次，且必须对非关系人小心保密，不再使用时，用以加密的文本应当要销毁，以防重复使用。usage unique

 

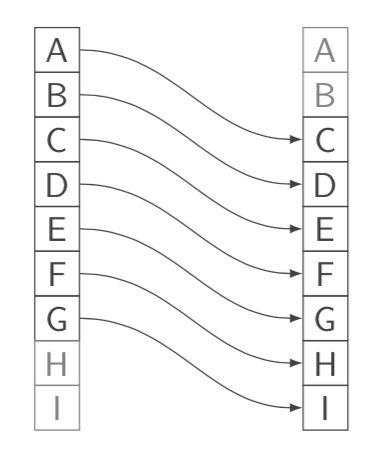
5. Enigma  恩尼格玛密码机

　　

德国密码机（1920），一种机电设备。

功能：加密/解密

使用：最初用于商业，后来主要被纳粹德国使用，并加强。

 

 

 

 

 

 

 

 

主要构成：

1. 键盘排列表
2. 串联3-4个转子（单字母替代）
3. 缺口→每个字母旋转一个或多个转子（多字母替代）
4. 反射器 - 加倍排列 - 使用相同的密钥进行加密和解密
5. 显示灯

 

 

 密钥：

同一台机器 - 同一组转子
使用的转子和初始位置
置换表的图表

 

---

【小结·补充】

Substitution mono-alphabétique  单字母替代法   

A1 → A2

分析解密方法：静态分析，频率统计

 

Substitution poly-alphabétique 多字母替代法

一些列替代规则（而非一个替代规则，几乎每个字母对应的替代方式都不同）

分析解密方法：找出密钥长度，Kasiski 测试，频率统计

 

Kerckhoffs's principle，柯克霍夫原则

也称为柯克霍夫假说、公理、或定律，由奥古斯特·柯克霍夫在19世纪提出：即使密码系统的任何细节已为人悉知，只要密匙（key，又称密钥或密钥）未泄漏，它也应是安全的。

 

---

Kasiski测试    http://tieba.baidu.com/p/776474651

 一、背景
公元16世纪晚期，法国外交官维吉尼亚（Vigenere）提出著名的维吉尼亚方阵密表和维吉尼亚密码(Vigenerecypher)，这是一种多表加密的替代密码。Vigenere密码的出现，使得先前对单表置换用的简单频率分析方法失效。
公元1863年，普鲁士少校卡西斯基（Kasiski）提出了Kasiski法，此方法从密钥的长度着手破解Vigenere密码。
二、基本思想
通常，用Vigenere密码加密，明文中的相同字母在密文中不会对应相同的字母。但是，如果两个相同字母序列间距正好是密钥长度的倍数时，也可能产生相同的密文序列。寻找重复出现的字母序列，并求其长度的过程被称为Kasiski试验，即Kasiski法。
Kasiski法在解密Vigenere密码时，利用的是多表体系的弱点：相同的明文字母组，在明文序列中间隔的字母数为d（d是密钥的长度）的倍数时，则明文字母组对应的密文字母组也必相同。反之则不一定，但相同的概率很大。如果将密文中相同字母组找出来，并对其间隔的距离进行研究，找出它们的最大公因子，则该因子是密钥长度的概率是较大的。
三、基本原理
基于Kasiski法的基本思想，Kasiski法测试过程如下：首先对密文中任意两个紧邻字符的出现位置进行统计，然后记下它们各次间出现的间隔。然后写出这些间隔对应数字的因数，最后对这些因数进行统计，一般来说，次数出现最多的几个因数极有可能就是密钥字符串的长度。其依据是，对于两个连续出现的字符在这次与下次出现的间隔极有可能是采用相同密钥加密形成的，从而这之间的间隔也极有可能就是密钥长度的倍数。
一般在使用Kasiski法测试密钥长度时，先搜索长度至少为3的相同的密文段，记录这些相同密文段到起始点之间的距离；假如得到如下几个距离X1,X2，…，猜测密钥长度m为这些Xi的最大公因子的因子。
四、应用步骤
1、在密文中标出重复的三个或多个字符结构；
2、对每一个字符结构，记下结构的起始位置；
3、计算相邻的起始点的距离；
4、对每个距离求出所有因数；
5、若使用多字母替换密码，则密钥的长度为步骤4种出现的某一因数；
五、应用举例
明文：we are discovered save yourself
密钥：deceptive
加密算法：Vigenere算法
密文：ZICVTWQNGRZGVTWAVZHCQYGLMGJ
测试过程：
1、在密文中标出重复的字符结构——VTW；
2、两个字符结构的起始位置分别为4和13；
3、两个起始点的距离是9；
4、9的因数有3和9；
5、根据步骤4出现的因数，确定密钥的可能长度是3位或9位。

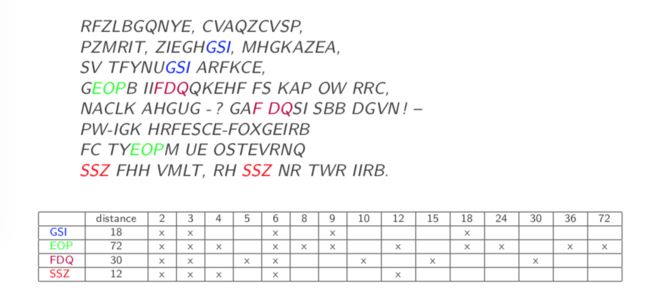
下面这个例子看的更清楚，通过多组重复出现的字段一起分析，找到公因子，便可确定密钥长度：

 

---

 弗里德曼试验 - 重合指数

弗里德曼试验由威廉·F·弗里德曼（William F. Friedman）于1920年代发明。他使用了重合指数（index of coincidence）来描述密文字母频率的不匀性，从而破译密码。指目标语言中两个任意字母相同的概率（英文中为0.067），指字母表中这种情况出现的概率（英文中为1/26=0.0385），从而密钥长度可以估计为：

其中，观察概率为

其中，c是指字母表的长度（英文为26），N指文本的长度，n₁到n_c是指密文的字母频率，为整数。

此方法只是一种估计，会随着文本长度的增加而更为精确。在实践中，会尝试接近此估计的多个密钥长度。^[7] 一种更好的方法是将密文写成矩阵形式，其中列数与假定的密钥长度一致，将每一列的重合指数单独计算，并求得平均重合指数。对于所有可能的密钥长度，平均重合指数最高的最有可能是真正的密钥长度。^[8] 这样的试验可以作为卡西斯基试验的补充。

---

 频率分析

一旦能够确定密钥的长度，密文就能重新写成多列，列数与密钥长度对应。这样每一列其实就是一个凯撒密码，而此密码的密钥（偏移量）则对应于维吉尼亚密码密钥的相应字母。与破译凯撒密码类似的方法，就能将密文破译。

柯克霍夫方法作为卡西斯基试验的改进，由奥古斯特·柯克霍夫（Auguste Kerckhoffs）提出。它将每一列的字母频率与转换后的明文频率相对应而得出每一列的密钥字母。一旦密钥中每一个字母都能确定，就能很简单地破译密文，从而得到明文。如果维吉尼亚字母表表格本身是杂乱而非按通常字母表顺序的话，那柯克霍夫方法就会无效，但卡西斯基试验和重复指数对于决定密钥长度仍旧是有效的。

 

---

 

现代密码学

计算机加密/解密， 二进制数字，bit大小，网络传输，数学应用。

三、对称加密

对称加密 - 私钥密码术

只有一把密钥，加密解密用这同一把。

已知的加密/解密算法

明文的特征：	两个策略：
1.大小	1.按bloc块加密
2.是全部还是局部	2.按flot流加密

 

加密类型 Stream cipher vs. Block cipher

序列（流）密码是对单个明文位（bit-by-bit）变换（transposition）的操作。

分组(块)密码是对一个大的明文块（block-by-block）进行固定变换的操作。

 

四、非对称加密

2对密钥：公钥，私钥　　

缓慢的算法

Exemple : RSA, El Gamal, ECC. . .

	加密时	验证时
公钥	加密	解密
私钥	解密	加密

（比如用自己的私钥加密自己的签名，用对方的公钥读取对方的签名）

 

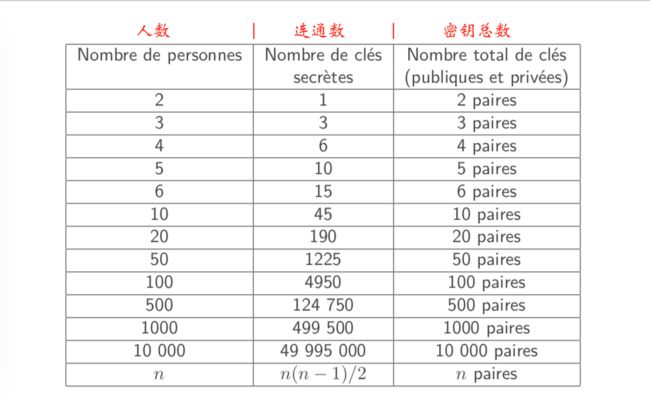
 对比【对称加密&非对称加密】

	对称加密	非对称加密
密钥数量	1	2对
常用的密钥大小	100bits（128bits）	2048bits（3072bits）-RSA/EI Gamal 200bis（256bits）-ECC
速度	快	慢
专用设备	是	很少
可靠性	弱	强

 

RSA 算法

RSA算法是第一个能同时用于加密和数字签名的算法，它是第一个既能用于数据加密也能用于数字签名的算法。由于大数分解计算量大，运算速度慢，

核心思想：对极大整数做因式分解，décomposition en facteurs premiers N。

 

ECC 椭圆加密算法

其数学基础是利用椭圆曲线上的有理点构成Abel加法群上椭圆离散对数的计算困难性。

优点

安全性高

• 有研究表示160位的椭圆密钥与1024位的RSA密钥安全性相同。

处理速度快

• 在私钥的加密解密速度上，ecc算法比RSA、DSA速度更快。
• 存储空间占用小。
• 带宽要求低。

五、哈希算法 hachage cryptographique

数据完整性确认和数据来源的真伪鉴定都是很重要的安全服务。实现这些安全服务的最好方法就是使用加密函数中的单项散列（Hash）函数。单项散列（Hash）函数是一种单项密码体制，它是一个从明文到密文的不可逆函数，也就是说，是无法解密的。通常应用在只需要加密、不需要解密的特殊应用场合。单项散列（Hash）函数H(M)作用于一任意长度的消息M，它返回一固定长度的散列值h:h=H(M)作为初始消息的独一无二的“数字指纹”，从而能保证数据的完整性和惟一性。

主要特征：不可逆，无冲突

典型算法：MD5， SHA

应用：身份验证，完整性验证。

 

典型算法：MD5

Message Digest Algorithm MD5（中文名为消息摘要算法第五版）为计算机安全领域广泛使用的一种散列函数，用以确保信息完整一致，提供消息的完整性保护。MD5的作用是让大容量信息在用数字签名软件签署私人密钥前被"压缩"成一种保密的格式（就是把一个任意长度的字节串变换成一定长的十六进制数字串）。

原理

对MD5算法简要的叙述可以为：MD5以512位分组来处理输入的信息，且每一分组又被划分为16个32位子分组，经过了一系列的处理后，算法的输出由四个32位分组组成，将这四个32位分组级联后将生成一个128位散列值。（反推是非常困难的）

 

方法

MD5典型应用是对一段信息（Message）产生信息摘要（Message-Digest），以防止被篡改。比如，很多软件在下载的时候都有一个文件名相同，文件扩展名为.md5的文件，在这个文件中通常只有一行文本，大致结构如： MD5 (tanajiya.tar.gz) = 38b8c2c1093dd0fec383a9d9ac940515

 

用户下载完该文件后，用我这个算法重新计算下载文件的MD5值，通过比较这两个值是否相同，就能判断下载的文件是否出错，或者说下载的文件是否被篡改了。

 

应用

1、一致性验证

2、数字签名

3、安全访问认证

多用于软件下载站、论坛数据库、系统文件安全等方面。

 

特点

1、压缩性：任意长度的数据，算出的MD5值长度都是固定的。

2、容易计算：从原数据计算出MD5值很容易。

3、抗修改性：对原数据进行任何改动，哪怕只修改1个字节，所得到的MD5值都有很大区别。

4、强抗碰撞：已知原数据和其MD5值，想找到一个具有相同MD5值的数据（即伪造数据）是非常困难的。

 

 

典型算法2：SHA 

安全散列算法（英语：Secure Hash Algorithm，缩写为SHA）是一个密码散列函数家族，是FIPS所认证的安全散列算法。能计算出一个数字消息所对应到的，长度固定的字符串（又称消息摘要）的算法。

 

MD5 与SHA-1 的比较

由于MD5 与SHA-1均是从MD4 发展而来，它们的结构和强度等特性有很多相似之处，表（1）是对MD5 与SHA-1 的结构比较。SHA-1与MD5 的最大区别在于其摘要比MD5 摘要长 32 比特。对于强行攻击，产生任何一个报文使之摘要等于给定报文摘要的难度：MD5 是2128 数量级的操作，SHA-1 是2160 数量级的操作。产生具有相同摘要的两个报文的难度：MD5是 264 是数量级的操作，SHA-1 是280 数量级的操作。因而,SHA-1 对强行攻击的强度更大。但由于SHA-1 的循环步骤比MD5 多（80:64）且要处理的缓存大（160 比特:128 比特），SHA-1 的运行速度比MD5 慢。

 

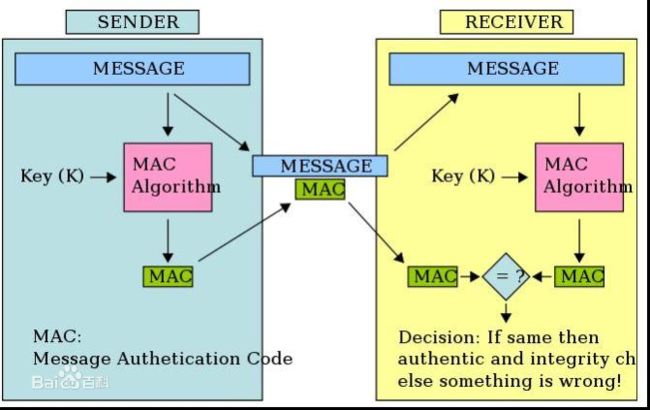
六、对称加密+哈希

Message Authentication Code（MAC） 

 

　　消息认证码（带密钥的Hash函数）:密码学中，通信实体双方使用的一种验证机制，保证消息 数据完整性，验证发送方身份的一种工具。构造方法由M.Bellare提出，安全性 依赖于Hash函数，故也称带密钥的Hash函数。 消息认证码是基于密钥和消息摘要所获得的一个值，可用于数据源发认证和完整性校验。

　　在发送数据之前，发送方首先使用通信双方协商好的散列函数计算其摘要值。 在双方共享的 会话密钥作用下，由摘要值获得消息验证码。之后，它和数据一起被发送。接收方收到报文后，首先利用会话密钥还原摘要值，同时利用散列函数在本地计算所收到数据的摘要值，并将这两个数据进行比对。若两者相等，则报文通过认证。

过程简述：

发送方 （拥有共享密钥K）

输入：信息，共享密钥K；

过程：信息+密钥K通过MAC 算法生成 MAC信息认证码1

发送：信息+MAC信息认证码

接收方（拥有共享密钥K）

收到：信息+MAC信息认证码，

核验过程：信息+密钥K通过MAC 算法生成 MAC信息认证码2

比较：自己生成的MAC2 和 收到的MAC1比较，如果一样，则通过验证。

 

【小结】对称加密+哈希：

目的：保密/ 身份验证/ 完整性验证

 

七、非对称加密+哈希：数字签名

目的：身份验证，完整性检测，不可撤销，不可重用。

基础：非对称加密，哈希。

　　数字签名（又称公钥数字签名、电子签章）是一种类似写在纸上的普通的物理签名，但是使用了公钥加密领域的技术实现，用于鉴别数字信息的方法。一套数字签名通常定义两种互补的运算，一个用于签名，另一个用于验证。

　　数字签名，就是只有信息的发送者才能产生的别人无法伪造的一段数字串，这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。

　　数字签名是非对称密钥加密技术与数字摘要技术的应用。　　

 

签名过程：

发送方：

1.用一个哈希函数从报文文本中生成报文摘要；

2.用自己的私人密钥对这个摘要进行加密，这个加密后的摘要即为 报文的数字签名；

3.将数字签名和报文一起发送给接收方，

 

接收方：

1.用与发送方 一样的哈希函数从接收到的原始报文中计算出报文摘要；（自己先用相同的哈希算出摘要）

2.接着再用发送方的公用密钥来对报文附加的数字签名进行解密；（用对方的公钥解出数字签名）

3.如果这两个摘要相同、那么接收方就能确认该数字签名是发送方的。（比较这个数字签名和自己算出的摘要，是否相同）

 

数字签名的两种功效：

　　 一是能确定消息确实是由发送方签名并发出来的，因为别人假冒不了发送方的签名。 二是数字签名能确定消息的完整性。因为数字签名的特点是它代表了文件的特征，文件如果发生改变，数字摘要的值也将发生变化。不同的文件将得到不同的数字摘要。 一次数字签名涉及到一个哈希函数、发送者的公钥、发送者的私钥。”

 

常见算法：

　　DSA, ElGamal, ECDSA, RSASSA-PSS...

 

八、Confidentialité persistante 持久保密

下面介绍的方法，不仅具备：保密，验证，完整性检测，还具备持久保密的特性。

完全正向保密（perfect forward secrecy）

　　这是信息安全中提出的观点。要求一个密钥只能访问由它所保护的数据；用来产生密钥的元素一次一换，不能再产生其他的密钥；一个密钥被破解，并不影响其他密钥的安全性。设计旨在长期使用密钥不能确保起安全性的情况下而不影响过去会话的保密性。

Diffie-Hellman密钥交换协议

迪菲－赫尔曼密钥交换（Diffie–Hellman key exchange，简称“D–H”） 是一种安全协议。它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道建立起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。

创建会话中密钥的过程：

1. Alice 和 Bob 通信， 双方都知道 p 和 g；
2. Alice 根据公式计算出A（幂为自己知道的a），Bob根据公式计算出B（幂为自己知道的b）；
3. 双方交换 A 和 B 的值；
4. 然后Alice用收到的B值再幂a次，Bob用收到的A值再幂b次（相当于g都幂次了a*b次，再mod p）；
5. 于是，Alice 和 Bob 都得到了双方相等的公共密钥。

这样，即使有中间人监听，也无法得到密钥，因为他无法知道a，b值。若想由A，B值推出幂次指数a或b是非常困难的。

 

九、证书

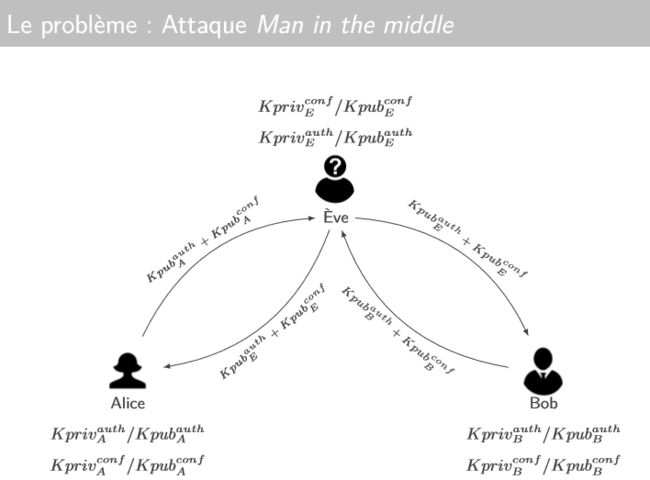
 背景问题：

 

 

 

 

 

 

 

解决方案 —— 证书

数字证书是一个经证书授权中心进行数字签名的包含公开密钥拥有者信息以及公开密钥的文件。最简单的证书包含一个公开密钥、名称以及证书授权中心的数字签名。数字证书还有一个重要的特征就是只在特定的时间段内有效。

数字证书是一种权威性的电子文档，可以由权威公正的第三方机构，即CA（例如中国各地方的CA公司）中心签发的证书，也可以由企业级CA系统进行签发。

证书包括：公钥（验证，完整性检验，保密）+ 身份证

证书拥有者的公钥
加密系统
证书名/证书域名
证书拥有者的名字和地址
证书有效期
证书发放者的名字
证书发放者的数字签名
证书编号

 

应用

数字证书可用于：发送安全电子邮件、访问安全站点、网上证券交易、网上招标采购、网上办公、网上保险、网上税务、网上签约和网上银行等安全电子事务处理和安全电子交易活动。

数字证书的类型

个人数字证书，主要用于标识数字证书自然人所有人的身份，包含了个人的身份信息及其公钥，如用户姓名、证件号码、身份类型等，可用于个人在网上进行合同签定、定单、录入审核、操作权限、支付信息等活动。

 

机构数字证书，主要用于标识数字证书机构所有人的身份，包含机构的相关信息及其公钥，如：企业名称、组织机构代码等，可用于机构在电子商务、电子政务应用中进行合同签定、网上支付、行政审批、网上办公等各类活动。

 

设备数字证书，用于在网络应用中标识网络设备的身份，主要包含了设备的相关信息及其公钥，如：域名、网址等，可用于VPN服务器、WEB服务器等各种网络设备在网络通讯中标识和验证设备身份。

此外，还有代码签名数字证书，是签发给软件提供者的数字证书，包含了软件提供者的身份信息及其公钥，主要用于证明软件发布者所发行的软件代码来源于一个真实软件发布者，可以有效防止软件代码被篡改。

 

典型证书举例

X.509

OpenPGP

 

CA认证

　　电子商务认证授权机构（CA, Certificate Authority），也称为电子商务认证中心，是负责发放和管理数字证书的权威机构，并作为电子商务交易中受信任的第三方，承担公钥体系中公钥的合法性检验的责任。

　　CA 也拥有一个证书（内含公钥）和私钥。网上的公众用户通过验证 CA 的签字从而信任 CA ，任何人都可以得到 CA 的证书（含公钥），用以验证它所签发的证书。

 

获取CA证书

　　如果用户想得到一份属于自己的证书，他应先向 CA 提出申请。在 CA 判明申请者的身份后，便为他分配一个公钥，并且 CA 将该公钥与申请者的身份信息绑在一起，并为之签字后，便形成证书发给申请者。

 

通过CA鉴别对方

　　如果一个用户想鉴别另一个证书的真伪，他就用 CA 的公钥对那个证书上的签字进行验证，一旦验证通过，该证书就被认为是有效的。

 

作用

Vérification de la signature  验证签名

Contrôle d’intégrité  完整性检验　　

Authentification 　真实性检验　　

Une contrainte : connaître la clé publique (certificat) de l’AC   前提是认识CA的公钥.

 

 

转载于:https://www.cnblogs.com/yanwenliqjl/p/8742568.html