多任务学习在推荐中的探索
多任务学习(Multi-task learning)在cv和nlp领域已经得到广泛的应用,无论是经典的maskrcnn—同时预测bounding box的位置和类别,还是称霸nlp的bert—预测某个单词和句子是否相关联,都属于多任务模型。在推荐中是基于隐式反馈来进行推荐的,用户对于推荐结果是否满意通常依赖很多指标(点击,收藏,评论,购买等),因此在排序中,我们需要综合考虑多个目标,尽可能使所有目标都达到最优。多任务学习是解决多目标排序问题的方案之一。
1 单任务学习和多任务学习
推荐中,基于隐式反馈的数据进行模型训练。数据数据的样本分布如下图所示,

点击、加入购物车、下单都是用户的积极反馈。训练中,这些都会作为正样本参与模型的学习。使用DNN+Embedding的模型,训练中点击,加购等都作为标签为1参数训练,给予他们不同的权重,加权在体现在损失函数中,即在原始交叉熵损失中,对于不同的正样本,在正样本损失中乘以不同的权值:
w ∗ y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) \textcolor{red}{w}*ylog\hat{y}+(1-y)log(1-\hat{y}) w∗ylogy^+(1−y)log(1−y^)
比如我们想优化订单,会给予订单样本比较大的权值,模型在学习过程中,会将重点放在订单部分,因为这部分会引起比较大的损失值,忽略点击样本。这样的情况下,会导致模型过于关注某一部分,模型学到的偏离整体样本分布,线上相当于用子空间去预测全空间的分布。
独立的单任务处理,忽略了问题之间所富含的丰富的关联信息。MTL可以找到各目标优化时的trade off。 比如Single Task 在优化转换的时候,会对点击带来负面效果,MTL可以降低甚至消除这个负面效果。常用多任务有hard和soft两种模式,

共享参数得过拟合几率比较低,hard parameter网络每个任务有自己的参数,模型参数之间的距离会作为正则项来保证参数尽可能相似。hard模式对于关联性比较强的任务,降低网络过拟合,提升了泛化效果。常用的是share bottom 的网络 可以共享参数,提高泛化(improving generalization)。
2 share bottom网络
将id特征embedding,和dense特征concat一起,作为share bottom网络输入,id

特征embedding可以使用end2end和预训练两种方式。预训练可以使用word2vec,GraphSAGE等工业界落地的算法,训练全站id embedding特征,在训练dnn或则multi task的过程中fine-tune。end2end训练简单,可以很快就将模型train起来,直接输入id特征,模型从头开始学习id的embedding向量。这种训练方式最致命的缺陷就是训练不充分,某些id在训练集中出现次数较少甚至没有出现过,在inference阶段遇到训练过程中没有遇到的id,就直接走冷启了。这在全站item变化比较快的情况下,这种方式就不是首选的方式。
多任务学习人工调的参数相对DNN较多,如上图所示,我们有三个损失,这三个损失怎么训练?三个子任务的输出,排序时如何使用?正负样本不均衡时,改如何处理?这三个问题分别对应了loss weight,output weight ,label weight。下面针对这三个问题,依次展开。
2.1 label weight
调整正样本的比例,对于正负样本分布不均衡的时候,该参数可以使得模型提高对正样本的关注,提高模型的召回,auc指标。


2.2 loss weight
调整损失的权重, 让共享层更关注某一个任务,也能解决一部分样本分布不均衡带来的过拟合。通常,MTL训练的过程中,是对多个子任务的损失线性加权:
L = ∑ i = 1 w i l i L=\sum_{i=1}w_il_i L=i=1∑wili
这样有个明显的缺点,就是这个 w i w_i wi需要很强的先验知识,人工预设,在训练的过程中保持不变。大家都知道,损失值在深度学习中的地位,直接决定了梯度的大小和传播,调参给出的权值很难保证我们给出的就是最优解,使得每个子任务都达到最优。这也是多任务学习一个主流的研究方向—pareto 最优解。这是一个经济学的概念,感兴趣的同学可以去了解一下,我会在下面附上相关的参考文献。言归正传,loss weight不合适,会导致正负样本严重不均衡的子任务会快出现过拟合的情况,如下图所示:
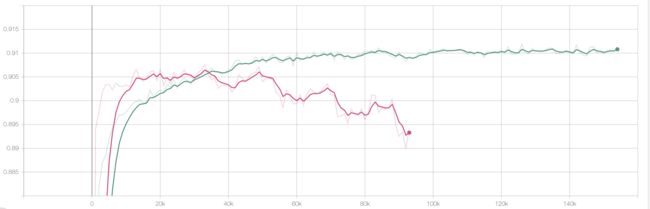
2.3 output weight
调整模型输出的权重组合。不同的权重值,影响排序时对应的子任务的重要性。对于输出的权重组合,可以利用grid search的思想,选出我们关心的离线评估指标最高的一个组合作为线上排序依据,在离线空间的组合逼近连续空间的最优值。最直接的做法可以将三个子任务的输出,在0到1区间,每隔0.1采样一个权值,在这1000组参数中,选择离线指标最高的一个组合作为最终的输出加权,下面是伪代码:
best_offline_score = 0
best_weight = None
for i in range(0,1.1,0.1):
for j in range(0,1.1,0.1):
for k in range(0,1.1,0.1):
score = task1_score*i+task2_score*j+task3_score * k
current_metric = calculate_offline_metrics(socre)
if current_metric > best_offline_score:
best_offline_score = current_metric
best_weight = [i, j, k] #记录最优的权值组合
3 MMoE与MTL结合
多任务模型对任务之间的相关性很敏感,如果子任务之前的关联性不大,采用share bottom的网络,share部分的参数,会有较大的噪音。通常,相似的子任务也拥有比较接近的底层特征,那么在多任务学习中,他们就可以很好地进行底层特征共享;而对于不相似的子任务,他们的底层表示差异很大,在进行参数共享时很有可能会互相冲突或噪声太多,导致多任务学习的模型效果不佳。
MMoE(Multi-gate Mixture-of-Experts)是 Google出品的文章,是在深度学习之父 Geoffrey Hinto提出的MoE(parsely-Gated Mixture-of-Experts layer)基础上改进。MoE 由许多 “专家” 组成,每个 “专家” 都有一个简单的前馈神经网络和一个可训练的门控网络(gating network),该门控网络选择 “专家” 的一个稀疏组合来处理每个输入,它可以实现自动分配参数以捕获多个任务可共享的信息或是特定于某个任务的信息。MMoE在MoE的基础上,添加多个gate,每个子任务对expert进行不同的加权,如果你熟悉cv中的SENET网络结构,那你对MMoE的这个思想就不会觉得有任何陌生感。

dense特征和id Embedding特征concat一起作为input输入,MMoE和MTL的结合有两种方式,input直接输入到MMoE,我们称之为直连的方式,这种方式的好处是可以很好的捕捉子任务之间的差异;另外一种方式是input先连接一个全连接,然后再接入MMoE中,当输入的特征维度比较高的时候,可以通过这种方式进行降维,连接到每个expert的输入变小,整体模型参数降低。原论文中在gate的部分添加了dropout和re -softmax,避免出现relu death的情况。



MMoE vs MTL 转化auc对比
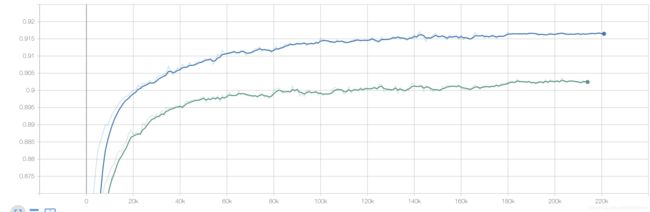
MMoE线上AB实验,相对MTL大概有5%左右的转化提升。
4 MMoE与贝叶斯结合
通过前面的实验,我们可以发现,MMoE是在share bottom的基础上改进的。MMoE 修改了网络共享参数的部分,所以一个很直观的想法就是,子任务之间是否也存在关联。简单举例来说,转化是发生在点击的条件下的,现有转化才有购买,但是我们现在的网络结构子任务之间是独立的。但是怎么构造子任务之间的关联呢?

如上图所示,可以将当前子任务的specific feature和上一个子任务的Embedding特征concat起来,作为子任务的输入。在这种情况下,就可以在预测转化的时候,是在考虑点击的条件概率下进行预测。
5 MTL调参经验
有监督学习问题中,最重要的选择是label,label决定了你做什么,决定了模型上限,而feature和model都是在逼近label。第一次直接拿原始DNN训练数据,直接训练MTL,离线指标好于DNN,但是线上却是负向的,最后发现是数据中噪声数据。MTL对数据准确性要求较高。
loss weight权重是正负样本比例的倒数,label weight 的正负样本调整成1:2。loss weight不合适很容易造成模型过拟合。网络深度不易过深(三层),推荐中过深的网落(高阶特征交叉)会有负向效果。
动态调整loss weight,模型在训练的过程中,自己学习权值。主要有两个优化方向,一是确保每个子任务的梯度在同一个量级,grad_norm 和 Weigh Losses,参考文章如下:
Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics
GradNorm: Gradient Normalization for Adaptive Loss Balancing in Deep Multitask Networks
二是利用Pareto optimization,求解多目标梯度优化(这个是未来主流的方向):
Multi-Task Learning as Multi-Objective Optimization
Multi-Gradient Descent for Multi-Objective Recommender Systems