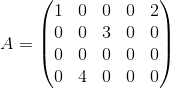奇异值分解(SVD)与PCA(主成分分析)
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统(稍后讲解),以及自然语言处理等领域,是很多机器学习算法的基石。下面将从SVD的原理、SVD的推导、分析SVD与PCA之间的关系等进行讲解,一步步到最后的推荐系统。
一、SVD原理
1.1 SVD定义
若A是一个m*n的矩阵,且![]() 可用等式:
可用等式:![]() 进行表示,则该过程被称之为奇异值分解。每个符号所代表的意义:
进行表示,则该过程被称之为奇异值分解。每个符号所代表的意义:
 对角线上的元素
对角线上的元素 被称为矩阵A的奇异值,非对角线上的元素为0.
被称为矩阵A的奇异值,非对角线上的元素为0.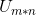 中第i列的向量被称为关于
中第i列的向量被称为关于 的左奇异向量,
的左奇异向量,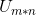 可以看成是对A的正交“输入”或分析的基向量,这些向量是矩阵
可以看成是对A的正交“输入”或分析的基向量,这些向量是矩阵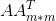 的特征向量。
的特征向量。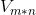 中第i列的向量被称为关于
中第i列的向量被称为关于 的右奇异向量,
的右奇异向量,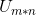 可以看成是对A的正交“输出”的基向量,这些向量是矩阵
可以看成是对A的正交“输出”的基向量,这些向量是矩阵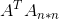 的特征向量。
的特征向量。
通常将奇异值由大到小进行排列,这样![]() 便能由A唯一确定,若对角阵
便能由A唯一确定,若对角阵![]() 不是满秩,奇异值分解不唯一。
不是满秩,奇异值分解不唯一。
1.2 SVD推导
1.2.1 特征值和特征向量
首先回顾下特征值和特征向量的定义:![]() 其中A是一个m*m的实对称矩阵,x是一个m维向量,则我们说λ是矩阵A的一个特征值,而x是矩阵A的特征值λ所对应的特征向量。
其中A是一个m*m的实对称矩阵,x是一个m维向量,则我们说λ是矩阵A的一个特征值,而x是矩阵A的特征值λ所对应的特征向量。
求出特征值和特征向量有什么好处呢? 就是我们可以将矩阵A特征分解。假设我们已经求出了矩阵A的m个特征值:![]() ,以及这m个特征值所对应的特征向量
,以及这m个特征值所对应的特征向量![]() 。若这m个特征向量线性无关,那么矩阵A就可以用下式的特征分解表示:
。若这m个特征向量线性无关,那么矩阵A就可以用下式的特征分解表示:![]() ,其中
,其中![]() 是这m个特征向量所张成的m*m维矩阵,而
是这m个特征向量所张成的m*m维矩阵,而![]() 为这m个特征值为主对角线的m*m维矩阵。
为这m个特征值为主对角线的m*m维矩阵。
一般我们会把![]() 的这m个特征向量标准化,即满足
的这m个特征向量标准化,即满足![]() 或者说
或者说![]() ,此时
,此时![]() 的m个特征向量为标准正交基,满足
的m个特征向量为标准正交基,满足![]() ,即
,即![]() , 也就是说
, 也就是说![]() 为酉矩阵。这样我们的特征分解表达式可以写
为酉矩阵。这样我们的特征分解表达式可以写![]() 的形式。
的形式。
注意要进行特征分解,矩阵A必须为方阵。那么如果A不是方阵,即行和列不相同时,我们还可以对矩阵进行分解吗?答案是可以,此时我们的SVD登场了。
1.2.2 SVD性质
由1.1的定义知,若A是一个m*n的矩阵,存在一个分解使得:![]() ,即奇异值分解。该过程可以用一个简单的图表示如下:
,即奇异值分解。该过程可以用一个简单的图表示如下:
![]()
那么我们如何求出SVD分解后的U,Σ,V这三个矩阵呢?
A的转置和A做矩阵乘法,那么会得到n*n的一个方阵![]() 。既然
。既然![]() 是方阵,我们就可以进行特征分解,得到的特征值和特征向量满足下式:
是方阵,我们就可以进行特征分解,得到的特征值和特征向量满足下式:![]() 。将
。将![]() 的所有特征向量组成一个n*n的矩阵V,就是我们SVD公式里面的V矩阵了。
的所有特征向量组成一个n*n的矩阵V,就是我们SVD公式里面的V矩阵了。
A和A的转置做矩阵乘法,那么会得到m*m的一个方阵![]() 。既然
。既然![]() 是方阵,我们就可以进行特征分解,得到的特征值和特征向量满足下式:
是方阵,我们就可以进行特征分解,得到的特征值和特征向量满足下式:![]() 。将
。将![]() 的所有特征向量张成一个m*m的矩阵U,就是我们SVD公式里面的U矩阵了。
的所有特征向量张成一个m*m的矩阵U,就是我们SVD公式里面的U矩阵了。
U和V我们都求出来了,现在就剩下奇异值矩阵Σ没有求出了。由于Σ除了对角线上是奇异值其他位置都是0,那我们只需要求出每个奇异值![]() 就可以了。
就可以了。
进过简单的推导,就可以用上述公式求出我们的每个奇异值,进而求出奇异值矩阵Σ。
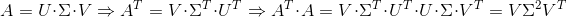 (即证明V为
(即证明V为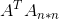 的特征向量组成的矩阵)。同理,可以证明
的特征向量组成的矩阵)。同理,可以证明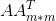 的特征向量矩阵为U。
的特征向量矩阵为U。- 已知
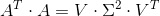 两边同时右乘:
两边同时右乘:

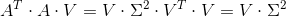 ,若
,若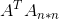 的特征值为
的特征值为 则:
则: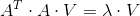 ,最终
,最终 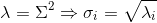 。也就是说,我们可以不用σi=Avi/ui来计算奇异值,也可以通过求出
。也就是说,我们可以不用σi=Avi/ui来计算奇异值,也可以通过求出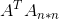 的特征值取平方根来求奇异值。
的特征值取平方根来求奇异值。
1.3 逆向SVD推导
由1.2性质知:
假设已知![]() ,反过来,则由右边推出左边。
,反过来,则由右边推出左边。
1.4 矩阵的奇异值分解意义
对于奇异值,跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值减少的特别快。在很多情况下前10%甚至1%的奇异值的和就占了全部奇异值之和的99%以上。也就是说,我们可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩。如下:
![]()
二、SVD与PCA区别
矩阵对向量的乘法,对应于该向量得旋转、伸缩。若对某向量只发生了伸缩而无旋转变化,则该向量是该矩阵的特征向量,伸缩比为特征值。
- PCA用来用来提取一个场的主要信息(即对数据集的列数——特征进行主成分分析),而SVD一般用来分析两个场的相关关系。
- PCA通过分解一个场的协方差矩阵(对特征),SVD是通过矩阵奇异值分解的方法分解两个场的协方差矩阵(特征、样本量)。
- PCA可用于特征的压缩、降维(去噪),SVD能够对一般矩阵分解,可用于个性化推荐。同时也可以用于NLP中的算法,比如潜在语义索引(LSI)等。
其实PCA几乎可以说是对SVD的一个包装,如果我们实现了SVD,那也就实现了PCA了。而且更好的地方是,有了SVD,我们就可以得到两个方向的PCA,如果我们对矩阵进行特征值的分解,只能得到一个方向的PCA。
三、SVD案例
3.1 求SVD分解
同3.2调用自定义函数,可求。
3.2 个性化推荐
假定Ben,Tom,John,Jerry对6种商品进行了评价,评价越高代表对越喜欢该产品。
| 商品\人 | Ben | Tom | John | Jerry |
|---|---|---|---|---|
| p1 | 5 | 5 | 0 | 5 |
| p2 | 5 | 0 | 3 | 4 |
| p3 | 3 | 4 | 0 | 3 |
| p4 | 0 | 0 | 5 | 3 |
| p5 | 5 | 4 | 4 | 5 |
| p6 | 5 | 4 | 5 | 5 |
将上述列表用矩阵来A表示: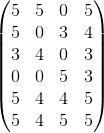 矩阵A为6行5列矩阵,对其进行奇异值分解。
矩阵A为6行5列矩阵,对其进行奇异值分解。
对A进行SVD分解,取k=2,![]() 。
。
import numpy as np
import matplotlib.pyplot as plt
def adaEig(A):
'''
按特征值从大到小的顺序求特征值、特征向量
'''
k = len(A)
eigVals,eigVects=np.linalg.eig(np.mat(A))
sorted_indices = np.argsort(eigVals)
topk_evecs = eigVects[:,sorted_indices[:-k-1:-1]]
topk_vals = eigVals[sorted_indices[:-k-1:-1]]
return topk_vals,topk_evecs
def adaEigTop_k(A,k):
'''
按特征值从大到小的顺序求前开个特征值、特征向量
'''
eigVals,eigVects=np.linalg.eig(np.mat(A))
sorted_indices = np.argsort(eigVals)
topk_evecs = eigVects[:,sorted_indices[:-k-1:-1]]
topk_vals = eigVals[sorted_indices[:-k-1:-1]]
return topk_vals,topk_evecs
def adaNew_V(N,U,sigm):
'''
计算新的V投影
'''
sigm_inv = np.linalg.inv(sigm) #求sigm的逆
V_new_tmp = np.dot(N.T,U)
V_new = np.dot(V_new_tmp,sigm_inv) #求出新的V_new 在V的投影
return V_new
# 将上述数据用A来表示
A = np.array([[5,5,0,5],[5,0,3,4],[3,4,0,3],[0,0,5,3],[5,4,4,5],[5,4,5,5]])
ATA = np.dot(A.T,A)
AAT = np.dot(A,A.T)
V_vals,V_evecs = adaEig(ATA)
U_vals,U_evecs = adaEig(AAT)
sigm = np.diag(np.sqrt(V_vals))
V = V_evecs
U = U_evecs
print('sigm\n',sigm)
print('\nV\n',V)
print('\nU\n',U)
'''
output:
sigm
[[17.71392084 0. 0. 0. ]
[ 0. 6.39167145 0. 0. ]
[ 0. 0. 3.09796097 0. ]
[ 0. 0. 0. 1.32897797]]
V
[[ 0.57098887 0.22279713 0.67492385 -0.41086611]
[ 0.4274751 0.51723555 -0.69294472 -0.26374238]
[ 0.38459931 -0.82462029 -0.2531966 -0.32859738]
[ 0.58593526 -0.05319973 0.01403201 0.80848795]]
U
[[-0.44721867 -0.53728743 0.00643789 -0.50369332 0.00343519 -0.46472718]
[-0.35861531 0.24605053 -0.86223083 -0.14584826 -0.10272674 0.21414493]
[-0.29246336 -0.40329582 0.22754042 -0.10376096 -0.25896385 0.82581681]
[-0.20779151 0.67004393 0.3950621 -0.58878098 -0.03424225 0.07138164]
[-0.50993331 0.05969518 0.10968053 0.28687443 0.79395785 -0.22519614]
[-0.53164501 0.18870999 0.19141061 0.53413013 -0.53928799 -0.01971168]]
'''
V_topk_vals,V_topk_evecs = adaEigTop_k(ATA,2)
U_topk_vals,U_topk_evecs = adaEigTop_k(AAT,2)
sigm_topk = np.diag(np.sqrt(V_topk_vals))
V_topk = V_topk_evecs
U_topk= U_topk_evecs
print('sigm_topk\n',sigm_topk)
print('\nV_topk\n',V_topk)
print('\nU_topk\n',U_topk)
'''
sigm_topk
[[17.71392084 0. ]
[ 0. 6.39167145]]
V_topk
[[ 0.57098887 0.22279713]
[ 0.4274751 0.51723555]
[ 0.38459931 -0.82462029]
[ 0.58593526 -0.05319973]]
U_topk
[[-0.44721867 -0.53728743]
[-0.35861531 0.24605053]
[-0.29246336 -0.40329582]
[-0.20779151 0.67004393]
[-0.50993331 0.05969518]
[-0.53164501 0.18870999]]
''' 对产品进行压缩,即U与sigm相乘
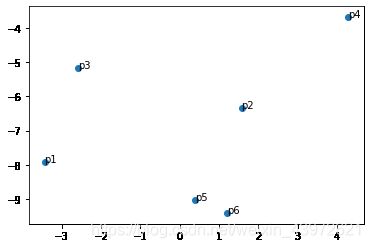
text = ['p1','p2','p3','p4','p5','p6',]
product_SVD = np.dot(U_topk,sigm_topk.T)
print(product_SVD)
plt.scatter(product_SVD[:,1].tolist(),product_SVD[:,0].tolist()) #画散点图
for i,txt in enumerate(text):
plt.annotate(txt,(product_SVD[:,1][i],product_SVD[:,0][i]))
plt.show()可视化显示:
对用户进行处理:
text = ['Ben','Tom','John','Fred']
customer_SVD = np.dot(V_topk,sigm_topk.T)
print(customer_SVD)
plt.scatter(customer_SVD[:,1].tolist(),customer_SVD[:,0].tolist()) #画散点图
for i,txt in enumerate(text):
plt.annotate(txt,(customer_SVD[:,1][i],customer_SVD[:,0][i]))
plt.show()可视化显示:
![]()
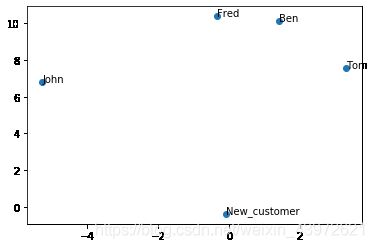
对于新的用户:
New_customer = np.array([5,5,0,0,0,5])
V_new = adaNew_V(New_customer,U_topk,sigm_topk)
text = ['Ben','Tom','John','Fred','New_customer']
customer_SVD = np.dot(V_topk,sigm_topk.T)
print(customer_SVD)
customer_SVD = np.vstack((customer_SVD,V_new))
plt.scatter(customer_SVD[:,1].tolist(),customer_SVD[:,0].tolist()) #画散点图
for i,txt in enumerate(text):
plt.annotate(txt,(customer_SVD[:,1][i],customer_SVD[:,0][i]))
plt.show()可视化显示:
通过上图,可查看New_customer最近的用户,也可以用余弦相似度来求New_customer与所有用户的距离,找到与New_customer最近的用户推荐,最后将最近用户的喜欢的商品与New_customer进行比较,从而实现个性化推荐。