密码学期末计算题复习

主要三大块

1.古典密码

移位密码：

E(x)= (x + K) mod 26
D(x)= (x - K) mod 26

代换密码

是指先建立一个替换表，加密时将需要加密的明文依次通过查表，替换为相应的字符，明文字符被逐个替换后，生成无任何意义的字符串，即密文，替代密码的密钥就是其替换表

欧拉函数：

设a ≥ 1，m ≥ 2, 如果gcd(a, m) = 1,则称a与m 互素，Zm中所有与m互素元素的个数用φ(m)来表示（函数φ称为欧拉函数）
例如φ(10) = 4，因为1,3,7,9均和10互质。
计算方法：
1.先化为标准分解式形式（化简成最小质数的幂乘积）：

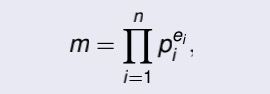
例如：

2.再依照下式规则计算


这其中 {1，5，7，11，13，17，19，23，25，29，31，35} 与36 互质，共计12 个

所以如果 m为质数 则 φ(m) = m-1

乘法逆元用拓展欧几里得求解详细过程：

例如求15 关于模26的乘法逆元：
15x = 1 mod 26 
这道题转化成15x - 26y = 1 ：

		解法如下：
		26 = 1× 15 + 11
		15 = 11×1 + 4
		11 = 4 × 2 + 3
		4 = 1 × 3 + 1
		3 = 1 × 3 
		
		∴ 1 = 4 – 3
    		  = 4 – (11 – 4×2)
    		  = 4×3 – 11
  	    	  = (15-11) ×3 - 11
  	    	  = 15×3 - 11×4
  	    	  = (26-11)×3 - 11 ×4
  	    	  = 26×3 - (26 - 15)×7
  	    	  =26×(-4) + 15×7
		∴ x = 7, y = −4 为此不定方程的一组整数解，15关于模26的乘法逆元为7

群Zm内所有元素关于模26的乘法逆元如下：

1：1
3：9
5：21
7：15
11：19
17：23
25：25

仿射密码：

假设密钥K= (7,3), 使用仿射密码体制加密单词hot并对得到的密文进行解密。
加密：

加密函数： E(x)= (7x + 3) (mod 26)
根据上面英文字母编码表得到X

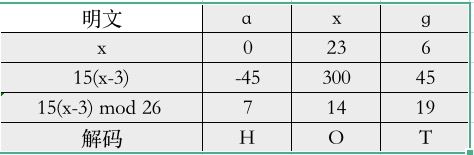
解密：

解密函数：
求得a的乘法逆元为15
D(x) = 15(x - 3) (mod 26)

希尔密码：

用希尔密码对明文串x = EastChinaNormalUniversity 进行加密，

密钥矩阵:

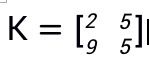
加密：
密文向量 = 明文向量 * 密钥矩阵 (mod 26)

1. 先将明文串对应英文字母编码表进行数字转化 4 0 18 19 2 7 8 13 0 13 14 17 12 0 11 20 13 8 21 4 17 18 8 19 24
   然后两两一组写成矩阵形式：
   
   做补0处理。

2. 接下来开始加密
   
   得到密文矩阵后，按照分组对应的向量转成字母：
   IK BX NB DH NN JD YE SR OB KB UJ HL W

解密同理用密钥矩阵的逆矩阵乘以加密结果。

定义在Zm上的矩阵求逆 ：

设矩阵

是定义在Zm上的矩阵,

举个例子：


这其中，9 关于模26 的乘法逆元为3.

2.对称密码体制

AES加密的工作模式

ECB（电子密码本模式）
之所以使用分组密码模式是因为分组密码只能处理定长的数据，如AES处理128bit，那么将明文切分成若干个128bit，分别加密。这种模式就是ECB模式，实际上有很明显的弱点，现在已经不被使用。

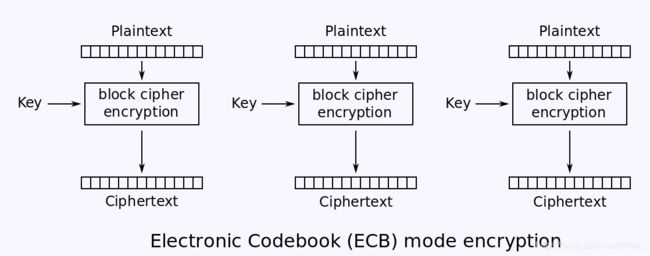
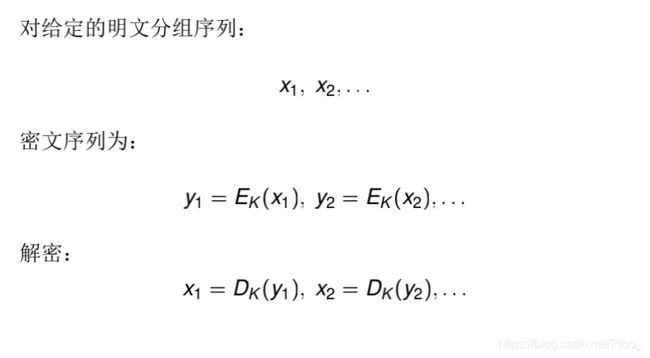
ECB模式是最简单的一种，它有很严重的问题，就是相同的明文会得到同样的密文。因为每个分组加密方式和密钥都相同，若分组明文相同，加密后密文也相同。

所以需要寻找一种模式，它至少得满足：

1. 相同的明文分组加密后密文不同。
2. 明文微小变化都能造成密文有很大变化。

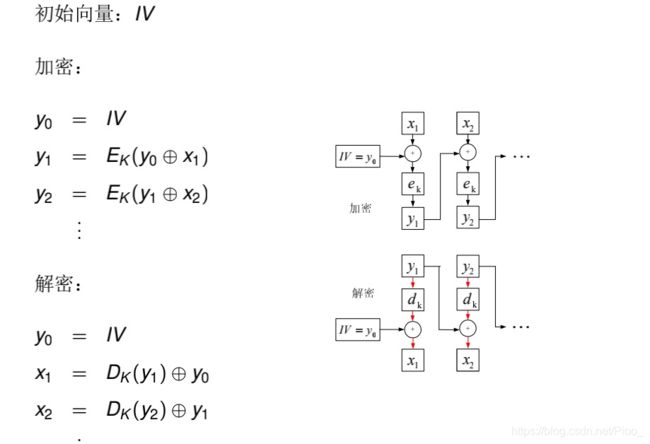
CBC模式（密码分组链接模式）
CBC模式由IBM发明与1976年，在CBC模式中，每个平文块先与前一个密文块进行异或后，再进行加密。在这种方法中，每个密文块都依赖于它前面的所有密文块。同时，为了保证每条消息的唯一性，在第一个块中需要使用初始化向量。

加密跟解密过程如下：

这里引入了初始化向量IV，因为第一组明文不存在"前一个密文"，一般来说每次加密都会生成随机值来做初始 化向量。

CFB模式 (密文反馈模式）
CFB又称密文反馈模式，前一个密文分组会被送入密码算法的输入端，再将输出的结果与明文做异或。与ECB和CBC模式只能够加密块数据不同，CFB能够将块密文（Block Cipher）转换为流密文。

加密跟解密过程如下：

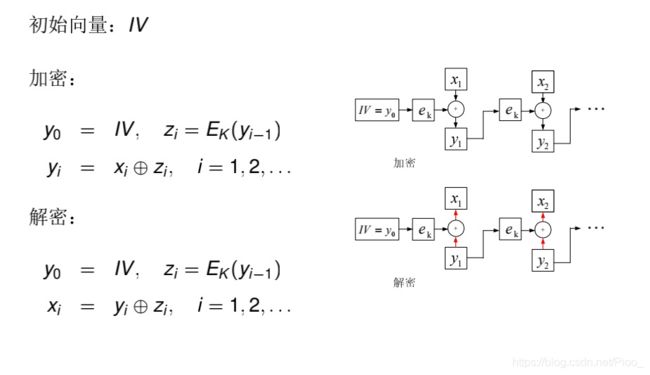
OFB模式（输出反馈模式）
OFB又称输出反馈模式，前一组密码算法输出会输入到下一组密码算法输入。先用块加密器生成密钥流，然后再将密钥流与明文流异或得到密文流，解密是先用块加密器生成密钥流，再将密钥流与密文流异或得到明文，由于异或操作的对称性所以加密和解密的流程是完全一样的。

3.非对称密码体制

拓展欧几里得求解同余方程组

1.求解同余方程组：
x ≡ 12 (mod 25)
x ≡ 9 (mod 26)
x ≡ 23 (mod 27)

以上方程组等价于 x = 25a + 12 = 26b + 9 = 27c + 23
移一下项 得：
① : 25a - 27c = 23-12 = 11
②: 26b - 25a = 12-9 = 3

首先对①式运用拓展欧几里得：

27 = 25×1 + 2
25 = 2×7 + 11
则： 
11 = 25 - 2×7
	 = 25 - (27-25) ×7
	 = 25×8 - 27×7
所以a=8, c=7 
代入x = 25a + 12  = 27c + 23 得：
x = 212

得到合并方程 x = 212 + 25 × 27t 即：x ≡ 212 (mod 675)
然后再跟x ≡ 9 (mod 26) 合并

x = 212 + 675t = 26b + 9
26b - 675t = 203
675 = 26×25+25
25 = 25×1
所以：  
203 = (26-25)×203
	= (26 - (675-26*25))×203
	=  26×5278 - 675×203
b=5278 , t=203
代入得x = 137237

得到合并方程 x = 137237 + 25 × 27×26t 即：x ≡ 137237 (mod 17550) , x=14387
x = 14387 + 17550n (n∈Z）

2.求解如下同余方程组：
13x ≡ 4 (mod 99)
15x ≡ 56 (mod 101)

这类同余方程组带着系数让人头大，但是也不妨碍使用拓展欧几里德，
首先去掉系数：
x ≡ 46 (mod 99)
x ≡ 98 (mod 101)
去系数步骤如下：这里列举利用二元一次不定方程方法：
13x ≡ 4 (mod 99) 转化为 13x-99y = 4
然后用拓展欧几里德：
13×46-99×6 = 4
x=46, y=6
所以不定方程13x-99y = 4 的所有解为
x=46 + 99t
y=6+13t
所以原同余方程解为：x ≡ 46 (mod 99)

消去系数后变成基本的求解同余方程组：
x = 99a+46 = 101a+98
消去x得： 99a - 101b = 52
拓展欧几里德走你：x = 7471 (mod 9999)
x = 9999 n + 7471 (n ∈ Z)

本原元求解

当a模n的阶为φ(n)，也就是说当且仅当x是φ(n)的倍数，使得ax ≡1(mod n)成立，此时称a为n的本原元。

假如求11的本原元：
步骤如下：
1.利用欧拉函数求φ(11) = 11-1 = 10
2.对10进行欧拉素因子分解 10 = 2 * 5
3.计算：2的平方 =4 mod 11 != 1 并且 2的5次方mod 11 !=1
则2 就是11的一个本原元

。。。这个来的有点轻松了，换一个数
求7的本原元：
1.φ(7) = 6
2. 6 = 2*3
3. 2的平方mod 7 !=1 ，但是 2的3次方mod7 =1, 所以2不是，
继续往下。。3的平方mod7!=1 并且3的3次方mod7!=1 所以3是7的一个本原元。

所以精髓就是
要恒成立~

RSA算法过程

一、密钥生成

1. 随机选择两个不相等的质数p和q，(这两个质数越大，就越难破解),我们为了方便举例，选取5和11

2. 计算p和q的乘积n 和欧拉函数φ(n)
   n = 5×11 = 55
   φ(n) = (p-1)(q-1) = 40

3. 随机选择一个整数b，条件是1< b < φ(n)，且b与φ(n) 互质…我们就选择3吧，方便计算

4. 计算b对于φ(n)的模反元素a
   a ≡ b^-1 (mod φ(n)) ≡ 3^-1 mod 40

   即：a×3 ≡ 1 mod 40
   (有小伙伴可能不知道怎么得来的。。a = n×40 + 3^-1 ,等式两边同乘3 即 3a = 3n × 40 + 1)

   这个时候就又到了我们熟悉的拓展欧几里德求解不定方程。。不熟的参考上一篇欧几里德算法、拓展欧几里德、中国剩余定理多练习一下。

   a×3 ≡ 1 mod 40 =>> 3a - 40y = 1

   得: a = 27, y = 2 是上述不定方程的一组解

5. 好了，到此整理一下Alice算的结果：
   公钥pk:(n = 55, b = 3)
   私钥sk:(p = 5,q = 11, a = 27)

   (实际应用中公钥和私钥的数据都采用ASN.1格式表达)

至此，我们的公私钥对生成阶段结束，下面开始加密

二、加密和解密
假设Bob要向Alice发送加密信息x，他就要用Alice的公钥 (n, b) 对x进行加密。
重点：x 必须是整数（字符串可以取ascii值），且x必须小于n。

这里我们例子中的n相对较小，所以我们需要将明文拆开进行多次加密：

假设我们加密明文 987654
一个一个来：
Ek(x) = x^b (mod n) = 9³ mod 55 = 14
Ek(x) = x^b (mod n) = 8³ mod 55 = 17
Ek(x) = x^b (mod n) = 7³ mod 55 = 13
Ek(x) = x^b (mod n) = 6³ mod 55 = 51
Ek(x) = x^b (mod n) = 5³ mod 55 = 15
Ek(x) = x^b (mod n) = 4³ mod 55 = 9

最终明文结果为：14 17 13 51 15 9

然后 Alice用自己的私钥进行解密：
Dk(y) = y^a (mod n) =14²⁷ mod 55 = 9
Dk(y) = y^a (mod n) =17²⁷ mod 55 = 8
Dk(y) = y^a (mod n) =13²⁷ mod 55 = 7
Dk(y) = y^a (mod n) =51²⁷ mod 55 = 6
Dk(y) = y^a (mod n) =15²⁷ mod 55 = 5
Dk(y) = y^a (mod n) =9²⁷ mod 55 = 4

计算出明文：987654

ElGamal加密算法

一.密钥生成

1. 对于Bob,首先要随机选择一个大素数p，且要求p-1有大素数因子。再选择一个模p的本原元α。将p和α公开。我们为了方便计算取p = 37,则Z37的一个本原元α = 2.

2. 随机选择一个整数d作为密钥，2≤d≤p-2 。我们选择d = 5,

3. 计算β=α^d mod p，β=2⁵ mod 37 = 32

二.加密
假设Alice 想发送消息 x = 29

1. 首先选取随机数k , 假设k = 7
   则： y1 = α^k mod p = 2⁷ mod 37 = 17
   y2 = x β^k mod p = 29×32⁷ mod 37 = 33
2. 将密文y = (17,33)发送给Bob

三.解密
Bob收到密文y = (17,33) 后恢复明文如下：
x = y2 (y1^d) ^-1 mod p
= 33 (17⁵) ^-1 mod 37
= 33×2 mod 37
= 29