CNN经典之LeNet网络+PyTorch复现

一、前情说明：

写在前面的话

本系列博客在于汇总CSDN的精华帖，类似自用笔记，不做学习交流，方便以后的复习回顾，博文中的引用都注明出处，并点赞收藏原博主。

本博客大致分为两部分，第一部是转载于其他平台的关于LeNet的讲解，第二部分是自己对网络的复现，包括：数据集加载和预处理，网络构建，模型测试等

二、CNN经典模型：LeNet

近几年来，卷积神经网络（Convolutional Neural Networks，简称CNN）在图像识别中取得了非常成功的应用，成为深度学习的一大亮点。CNN发展至今，已经有很多变种，其中有几个经典模型在CNN发展历程中有着里程碑的意义，它们分别是：LeNet、Alexnet、Googlenet、VGG、DRL等，接下来将分期进行逐一介绍。
在之前的文章中，已经介绍了卷积神经网络（CNN）的技术原理，细节部分就不再重复了，有兴趣的同学再打开链接看看（卷积神经网络详解），在此简单回顾一下CNN的几个特点：局部感知、参数共享、池化。

1、局部感知

人类对外界的认知一般是从局部到全局、从片面到全面，类似的，在机器识别图像时也没有必要把整张图像按像素全部都连接到神经网络中，在图像中也是局部周边的像素联系比较紧密，而距离较远的像素则相关性较弱，因此可以采用局部连接的模式（将图像分块连接，这样能大大减少模型的参数），如下图所示：

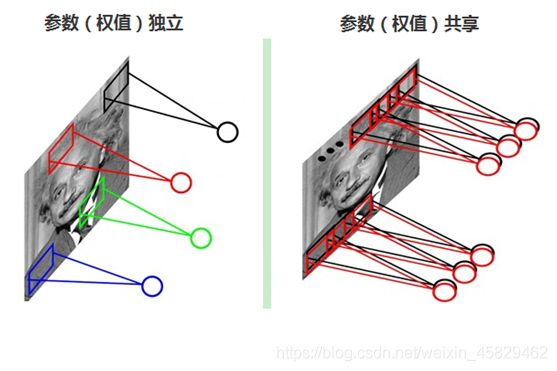
2、参数（权值）共享

每张自然图像（人物、山水、建筑等）都有其固有特性，也就是说，图像其中一部分的统计特性与其它部分是接近的。这也意味着这一部分学习的特征也能用在另一部分上，能使用同样的学习特征。因此，在局部连接中隐藏层的每一个神经元连接的局部图像的权值参数（例如5×5），将这些权值参数共享给其它剩下的神经元使用，那么此时不管隐藏层有多少个神经元，需要训练的参数就是这个局部图像的权限参数（例如5×5），也就是卷积核的大小，这样大大减少了训练参数。如下图

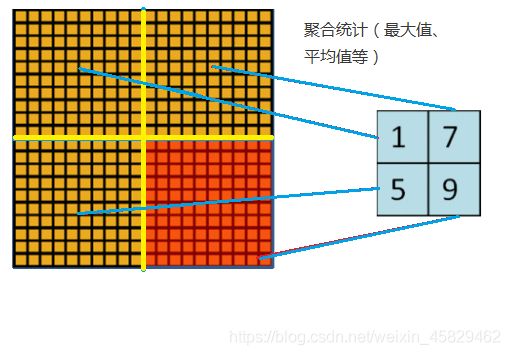
3、池化

随着模型网络不断加深，卷积核越来越多，要训练的参数还是很多，而且直接拿卷积核提取的特征直接训练也容易出现过拟合的现象。回想一下，之所以对图像使用卷积提取特征是因为图像具有一种“静态性”的属性，因此，一个很自然的想法就是对不同位置区域提取出有代表性的特征（进行聚合统计，例如最大值、平均值等），这种聚合的操作就叫做池化，池化的过程通常也被称为特征映射的过程（特征降维），如下图：

回顾了卷积神经网络（CNN）上面的三个特点后，下面来介绍一下CNN的经典模型：手写字体识别模型LeNet5。
LeNet5诞生于1994年，是最早的卷积神经网络之一， 由Yann LeCun完成，推动了深度学习领域的发展。在那时候，没有GPU帮助训练模型，甚至CPU的速度也很慢，因此，LeNet5通过巧妙的设计，利用卷积、参数共享、池化等操作提取特征，避免了大量的计算成本，最后再使用全连接神经网络进行分类识别，这个网络也是最近大量神经网络架构的起点，给这个领域带来了许多灵感。
LeNet5的网络结构示意图如下所示：

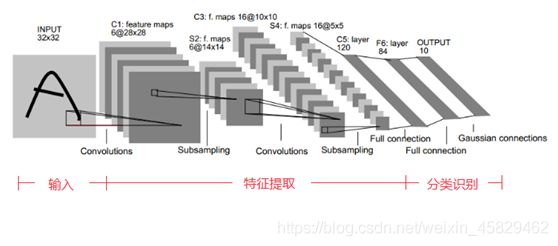
LeNet5由7层CNN（不包含输入层）组成，上图中输入的原始图像大小是32×32像素，卷积层用Ci表示，子采样层（pooling，池化）用Si表示，全连接层用Fi表示。下面逐层介绍其作用和示意图上方的数字含义。

1、C1层（卷积层）：6@28×28

该层使用了6个卷积核，每个卷积核的大小为5×5，这样就得到了6个feature map（特征图）。

（1）特征图大小

每个卷积核（5×5）与原始的输入图像（32×32）进行卷积，这样得到的feature map（特征图）大小为**（32-5+1）×（32-5+1）= 28×28**
卷积过程如下图所示：

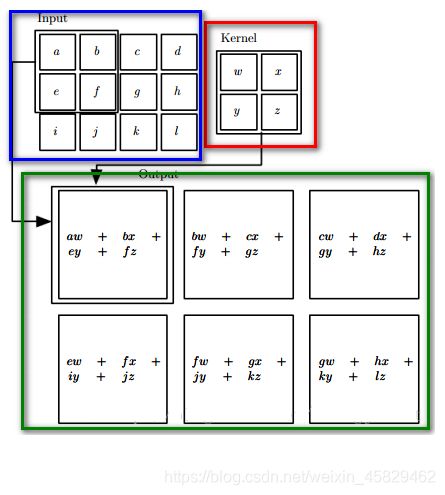
卷积核与输入图像按卷积核大小逐个区域进行匹配计算，匹配后原始输入图像的尺寸将变小，因为边缘部分卷积核无法越出界，只能匹配一次，如上图，匹配计算后的尺寸变为Cr×Cc=（Ir-Kr+1）×（Ic-Kc+1），其中Cr、Cc，Ir、Ic，Kr、Kc分别表示卷积后结果图像、输入图像、卷积核的行列大小。

（2）参数个数

由于参数（权值）共享的原因，对于同个卷积核每个神经元均使用相同的参数，因此，参数个数为（5×5+1）×6= 156（如果都是独立参数，应该是28×28×（5×5×1）×6），其中5×5为卷积核参数，1为偏置参数bias（这个可以翻到神经元激活那部分，Y=WX+b，相当于加了一个截距），

（3）连接数

卷积后的图像大小为28×28，因此每个特征图有28×28个神经元，每个卷积核参数为（5×5+1）×6，因此，该层的连接数为（5×5+1）×6×28×28=122304

2、S2层（下采样层，也称池化层）：6@14×14

（1）特征图大小

这一层主要是做池化或者特征映射（特征降维），池化单元为2×2，因此，6个特征图的大小经池化后即变为14×14。回顾本文刚开始讲到的池化操作，池化单元之间没有重叠，在池化区域内进行聚合统计后得到新的特征值，因此经2×2池化后，每两行两列重新算出一个特征值出来，相当于图像大小减半，因此卷积后的28×28图像经2×2池化后就变为14×14。
这一层的计算过程是：2×2 单元里的值相加，然后再乘以训练参数w，再加上一个偏置参数b（每一个特征图共享相同的w和b)，然后取sigmoid值（S函数：0-1区间），作为对应的该单元的值。卷积操作与池化的示意图如下：
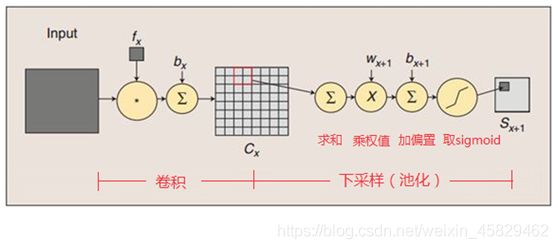（2）参数个数

S2层由于每个特征图都共享相同的w和b这两个参数，因此需要2×6=12个参数（为什么是2×6？？？博主也找了很多资料，后面了解到池化层的采样方式为：2*2区域的4个值相加，乘以一个可训练参数，再加上一个偏置参数，结果通过Sigmoid非线性化个人感觉也应该和LeNet采用的最大池化有关，也就是2*2的区域中找到是最大特征值，也就是卷积核的作用是找数，而不是参与运算，有不同意见的大佬可以交流指点）

3、C3层（卷积层）：16@10×10

C3层有16个卷积核，卷积模板大小为5×5。

（1）特征图大小

与C1层的分析类似，C3层的特征图大小为（14-5+1）×（14-5+1）= 10×10

（2）参数个数

需要注意的是，C3与S2并不是全连接而是部分连接，有些是C3连接到S2三层、有些四层、甚至达到6层，通过这种方式提取更多特征，连接的规则如下表所示：

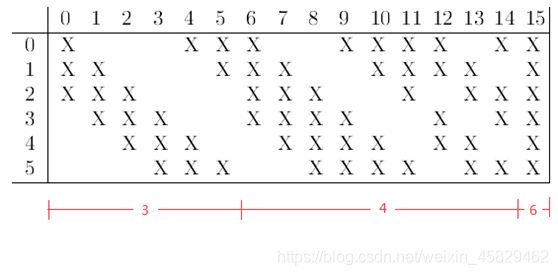
例如第一列表示C3层的第0个特征图（feature map）只跟S2层的第0、1和2这三个feature maps相连接，计算过程为：用3个卷积模板分别与S2层的3个feature maps进行卷积，然后将卷积的结果相加求和，再加上一个偏置，再取sigmoid得出卷积后对应的feature map了。其它列也是类似（有些是3个卷积模板，有些是4个，有些是6个）。因此，C3层的参数数目为（5×5×3+1）×6 +（5×5×4+1）×9 +5×5×6+1 = 1516

（3）连接数

卷积后的特征图大小为10×10，参数数量为1516，因此连接数为1516×10×10= 151600

4、S4（下采样层，也称池化层）：16@5×5

（1）特征图大小

与S2的分析类似，池化单元大小为2×2，因此，该层与C3一样共有16个特征图，每个特征图的大小为5×5。

（2）参数数量

与S2的计算类似，所需要参数个数为16×2 = 32

（3）连接数

连接数为（2×2+1）×5×5×16 = 2000

5、C5层（卷积层）：120

（1）特征图大小

该层有120个卷积核，每个卷积核的大小仍为5×5，因此有120个特征图。由于S4层的大小为5×5，而该层的卷积核大小也是5×5，因此特征图大小为（5-5+1）×（5-5+1）= 1×1。这样该层就刚好变成了全连接，这只是巧合，如果原始输入的图像比较大，则该层就不是全连接了。

（2）参数个数

与前面的分析类似，本层的参数数目为120×（5×5×16+1） = 48120

（3）连接数

由于该层的特征图大小刚好为1×1，因此连接数为48120×1×1=48120

6、F6层（全连接层）：84

（1）特征图大小

F6层有84个单元，之所以选这个数字的原因是来自于输出层的设计，对应于一个7×12的比特图，如下图所示，-1表示白色，1表示黑色，这样每个符号的比特图的黑白色就对应于一个编码。

该层有84个特征图，特征图大小与C5一样都是1×1，与C5层全连接。

（2）参数个数

由于是全连接，参数数量为（120+1）×84=10164。跟经典神经网络一样，F6层计算输入向量和权重向量之间的点积，再加上一个偏置，然后将其传递给sigmoid函数得出结果。
（3）连接数

由于是全连接，连接数与参数数量一样，也是10164。

7、OUTPUT层（输出层）：10

Output层也是全连接层，共有10个节点，分别代表数字0到9。如果第i个节点的值为0，则表示网络识别的结果是数字i。

（1）特征图大小

该层采用径向基函数（RBF）的网络连接方式，假设x是上一层的输入，y是RBF的输出，则RBF输出的计算方式是：

上式中的Wij的值由i的比特图编码确定，i从0到9，j取值从0到7×12-1。RBF输出的值越接近于0，表示当前网络输入的识别结果与字符i越接近。

（2）参数个数

由于是全连接，参数个数为84×10=840

（3）连接数

由于是全连接，连接数与参数个数一样，也是840

通过以上介绍，已经了解了LeNet各层网络的结构、特征图大小、参数数量、连接数量等信息，下图是识别数字3的过程，可对照上面介绍各个层的功能进行一一回顾：

转载于：https://my.oschina.net/u/876354/blog/1632862

三、LeNet实现Cifer分类

LeNet图像分类器步骤如下：

CIFAR10简介
加载和预处理数据集
定义LeNet神经网络
定义损失函数
在训练数据上训练并测试网络

Cifer数据集

CIFAR-10数据集由10类32*32的彩色图片组成， 一共包含60000张图片，每一类包含6000张图片。
下图显示的是数据集的类， 以及每一类中随机挑选的10张图片:

图来自：https://blog.csdn.net/qq_37766812/article/details/105532468

加载和预处理数据集

import torchvision.transforms as transforms
from torch.autograd import Variable
import torch
import torchvision as tv
from torch import nn, optim

################################数据加载和预处理#########################
transform = transforms.Compose([
    transforms.ToTensor(), # 转化为Tensor
    transforms.Normalize((0.5, 0.5, 0.5),(0.5, 0.5, 0.5)), # 归一化处理
])

# 定义了我们的训练集，名字就叫trainset，至于后面这一堆，其实就是一个类：
# torchvision.datasets.CIFAR10( )也是封装好了的，就在前面系列提到的torchvision.datasets
# 加载已经下载好的数据集
trainset = tv.datasets.CIFAR10(
    root = 'E:/pytorch/动手学深度学习/',
    train = True,
    download = False,
    transform = transform
)

trainloader = torch.utils.data.DataLoader(
    trainset,
    batch_size = 16,
    shuffle = True,
    num_workers = 2
)
#测试集
testset = tv.datasets.CIFAR10(
    'E:/pytorch/动手学深度学习/',
    train = False,
    download = False,
    transform = transform
)

testloader = torch.utils.data.DataLoader(
    trainset,
    batch_size = 16,
    shuffle = True,
    num_workers = 2
)

# 类别信息也是需要我们给定的
classes = ('plane', 'car', 'bird', 'cat','deer', 'dog', 'frog', 'horse', 'ship', 'truck')

代码的具体作用和注解在之前系列已说明，详见https://blog.csdn.net/weixin_45829462/article/details/106568309

结果如下：

Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./data\cifar-10-python.tar.gz


100%|██████████████████████████████████████████████████████████████▉| 170434560/170498071 [05:20<00:00, 1334098.03it/s]

Files already downloaded and verified
Files already downloaded and verified

定义LeNet神经网络

class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        self.conv = nn.Sequential(
            # 对卷积层进行Sequential封装
            nn.Conv2d(3, 6, 5),
            # 卷积层“3”表示输入图片为单通道，“6”表示输出通道数,‘5’表示卷积核为5*5
            nn.Sigmoid(),
            # 使用Sigmoid激活
            nn.MaxPool2d(2, 2),
            # 使用最大池化层，卷积核大小为2*2，步长为2


            nn.Conv2d(6, 16, 5),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2)
        )
        self.fc = nn.Sequential(
            # 全连接层，y=Wx+b，in_channels=16*5*5
            nn.Linear(16*5*5, 120),
            nn.Sigmoid(),

            nn.Linear(120, 84),
            nn.Sigmoid(),

            nn.Linear(84,10)
        )

    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.view(img.shape[0], -1))
        return output
net = LeNet()
print(net)

结果如下：

LeNet(
  (conv): Sequential(
    (0): Conv2d(3, 6, kernel_size=(5, 5), stride=(1, 1))
    (1): Sigmoid()
    (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
    (3): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
    (4): Sigmoid()
    (5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (fc): Sequential(
    (0): Linear(in_features=400, out_features=120, bias=True)
    (1): Sigmoid()
    (2): Linear(in_features=120, out_features=84, bias=True)
    (3): Sigmoid()
    (4): Linear(in_features=84, out_features=10, bias=True)
  )
)

定义损失函数和优化器

###############定义损失函数和优化器(loss和optimiter)#################
criterion = nn.CrossEntropyLoss() # 交叉熵损失函数
# 训练算法使⽤用SGD算法
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)

Pytorch学习之Cifer实战四·激活函数+损失函数+优化器详解可参见此文章：
https://blog.csdn.net/weixin_45829462/article/details/106595624

训练和评估网络：

for epoch in range(100):
    # 指定训练的批次
    start = time.time()
    correct = 0.0
    # 预测正确的图片数
    total = 0.0
    # 总共参与测试的图片数，也初始化为0
    running_loss = 0.0
    # 定义loss，并初始为0，方便后面计算后输出
    for i, data in enumerate(trainloader, 0):
        # enumerate()用于可迭代\可遍历的数据对象组合为一个索引序列，
        # 同时列出数据和数据下标.上面代码的0表示从索引从0开始，假如为1的话，那索引就从1开始。
        inputs, labels = data
        # data是从enumerate返回的data，包含数据和标签信息，分别赋值给inputs和labels
        inputs, labels = Variable(inputs), Variable(labels)
        # 之所以要使用Variable，是因为这个函数包含了对Tensor的所有操作，包括自动求导和实现反向传播等
        optimizer.zero_grad()
        # 梯度清零

        # 前向传播＋反向传播 forword + backward
        outputs = net(inputs)
        # 把数据输进网络alexnet，这个alexnet()在第二部分我们已经定义了
        loss = criterion(outputs, labels)
        # 计算损失值,criterion是损失函数包装器，我们在第四节也讲过，
        # criterion(outputs, labels)指的是卷积操作后outputs和labels之间的差异值
        # 记住这个outputs输出的并非tensor，而是ship、airplane这类的便签信息
        loss.backward()
        # loss进行反向传播
        # 更新参数
        optimizer.step()

        # running_loss += loss.data[0]
        running_loss += loss.item()


    with torch.no_grad():
        for data in testloader:
            # 循环每一个batch，之前我们定义了每个batch_size=16
            images, labels = data
            if isinstance(net, torch.nn.Module):
                # 判断网络是否运行中
                net.eval()
                # 是的话暂停网络训练
                outputs = net(Variable(images))
                # 输入网络进行测试
                # images其实是tensor矩阵，我们在第二部分输出过
                _, predicted = torch.max(outputs.data, 1)
                correct += (predicted == labels)
                # 更新正确分类的图片的数量，(predicted ==labels)是一个bool类型，
                # (predicted ==labels).sum()将所有预测正确的值相加，得到的仍是tensor类别的int值
                total += labels.size
                # 更新测试图片的数量，labels.size(0)=1，等价于total += 1
                net.train()

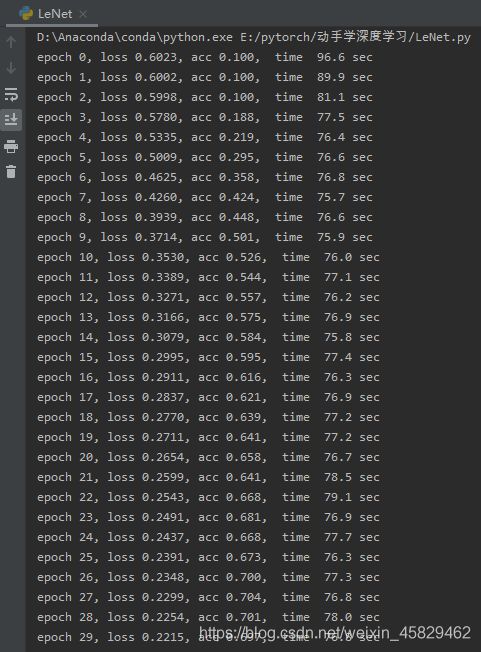
    print('epoch %d, loss %.4f, acc %.3f,  time % .1f sec'
          % (epoch, running_loss / 12000, correct / total, time.time() - start))
print('Finished Training')
# 每迭代一次计算一次loss，然后清零

结果如下：