微积分基本概念

选择题

1.特值法

大题

1.题目之间的逻辑关系：第二小题必用第一小题结论

2.伪证

函数 极限 连续

集合

区间

邻域

映射

函数

函数运算

反函数

奇函数

偶函数

周期函数

数列

基本初等函数：三角函数，指数函数，对数函数，幂函数

初等函数

函数关系式

分段函数

复合函数

隐式函数：

参数函数

数列极限

自变量趋于无穷大函数极限

自变量趋于有限值函数极限

单侧极限

数列极限和函数极限关系

无穷大量

无穷小量

无穷小运算性质：1.无穷小+有限无穷小=无穷小  2.无穷小*有界变量=无穷小

函数极限和无穷小关系

极限

局部有界性、唯一性、局部保号性、不等式性质（保序性）

洛必达：太过复杂、无法判断、没有办法，直接洛

极限=0，分母为0项数可消去

直接代入

0/0：洛必达；因式分解；等价无穷小

无穷/无穷：洛必达

无穷/无穷：通分

分子分母有理化

k阶无穷小

1^无穷：e为底 ，分子等价无穷小+只有一个可以泰勒展开的式子，其它全是x^n，直接展开

极限运算

极限存在准则

极限不存在：   无穷

夹逼准则：适当放缩

单调有界准则：单调有界数列必有极限

无穷小比较

连续性

间断点

连续函数

 

罗尔定理证明等式：化为f(x)=0，找出原函数F(x)=0，F(左)=F(右)，就OK

拉格朗日中值定理：割线=切线，f(a)-f(b)=f '(x)(a-b)

 

连续函数性质：如果一个连续函数在区间内有相反符号的值，那么它在该区间内有根存在

连续函数运算：连续*不连续=不连续

初等函数连续性

 

一元函数微分学

导数：
单侧导数：  >0右导数，<0左导数
导数的几何意义
函数可导与连续的关系：可导？x0是否有定义，即f(x0)是否存在；其次bai判断f(x0)是否连续，即f(x0-), f(x0+), f(x0)三者是否相等；再次判断函数在x0的左右导数是否存在且相等，即f‘(x0-)=f'(x0+)
导数的四则运算法则
反函数的求导法则

反函数的求导=原函数导数的倒数
复合函数的求导法则
导数的基本公式
隐函数及参数式函数的导数
隐函数的导数

指数含有xy：两边底数取e

知导数求极限：定义

参数式函数的导数
相关变化率问题
高阶导数

莱布尼兹公式

sinax cosbx x^a  1/x  Inx  e^ax   In(a+x)   1/a+x 

函数的微分
微分的概念

       --->          ---->

    dy=线性主部   dx=自变量增量   x0=某处

   

微分的运算法则
函数的线性近似
微分中值定理…
函数的极值及其必要条件
微分中值定理

罗尔中值定理：f(x)   g(x)在[a,b]连续 (a,b)可导，

不定型的极限
泰勒公式
几个常用的麦克劳林公式

 

e  1 sin cos

1/1+x   1/1-x   arctanx  In(1+x)

泰勒公式的应用
函数单调性的判定法
函数极值的判定法
最大值与最小值问题

函数的凸性与曲线的拐点
函数作图
曲线的渐近线

 

水平：limx->无穷，A

竖直：limx->间断点，f(x)->无穷

斜：limx->无穷，f(x)/x=k       limx->无穷，f(x)-xk=b

曲线的曲率  

曲率半径：R=1/k

弧微分
曲率

一元函数积分学

定积分

判断部分函数奇偶性

牛莱公式
函数可积的充分条件：连续   或者   有界+第一种间断点
定积分的几何意义：面积
定积分的性质：可加性，积分上下限反转提负号，常数可提

不定积分的性质：全体求导=内部函数    ；内部求导=内部函数的原函数   
微积分基本定理

 

估值定理：

换元积分法
不定积分的换元积分法

定积分的换元积分法
分部积分法
顺序：

不定积分的分部积分法

定积分的分部积分法
 

x^2+-a积分

+a  x=atant

-a  x=a sect

a-x^2  x=a sint

有理函数的积分

分母项数一定要大于分子，否则多项式除法

                               ：                

积分上限函数：；求导=f(x)   ；   求导=

积分中值定理： 

三角函数有理式的积分

sc=1/2(sin+sin)

ss=-1/2(c-c)

cc=1/2(c+c)

和 使用二倍角公式降幂

 

  
反常积分

广义牛莱
无穷区间上的反常积分

无界函数的反常积分

伽玛函数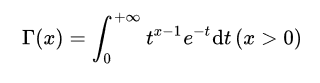Γ（x+1）=xΓ(x)       Γ（x+1）=x！      Γ(1)=1  Γ(0)=正无穷  Γ(1/2)=根号π
定积分的几何应用
微元法
求平面图形的面积

求体积
函数的平均值与均方根
 

常微分方程

微分方程的基本概念

一阶微分方程

x|y：直接积分
y/x：u=y/x   dy/dx=u+x*du/dx
：

高阶微分方程

特征方程：--->

型：直接积分

型：u=y^(n-1)  化成     后直接积分
只有y：

y->r   求解r  

单实根r                                            k重实根r             

单复根a+bi     k重复根a+bi     

通解Y=C+对应解之和

有y有x：

1. 求通解   ：   y->r   求解r   单实根  k重实根   通解Y=C+对应解之和

2.设特解，求导后代入微分方程出系数

二阶齐次线性方程
二阶齐次线性方程解的性质与结构

二阶常系数齐次线性方程的解法
二阶非齐次线性方程
二阶非齐次线性方程解的性质与结构

二阶常系数非齐次线性方程的解法

欧拉方程