2021算法竞赛入门班第一节课枚举贪心习题

1.明明的随机数

链接
题目大意就是：输入n个1到1000之内的数，然后去重排序输出，即可

#include
using namespace std;
set<int> s;  //set集合自动排序去重
int n , num;
int main(){
     
    cin>>n;
    while(n--){
     
        cin>>num;
        s.insert(num);
    }
    cout<<s.size()<<endl;
    for(auto& ans :s ){
     
        cout<<ans<<" ";
    }
}

2.回文日期

链接
题目大意就是：给你两个日期，判断两个日期中有多少个日期是回文的（20100102）
因为需要回文，20100102我们可以发现月份和日期反过来就可以得到年份2010，我们只需要判断反过来的年是否在两个日期之间即可。

#include
using namespace std;
int day[13] = {
     0,31,29,31,30,31,30,31,31,30,31,30,31};  //每月对应的天数
int ans;
int main(){
     
    int yy,mm,dd;
    int y,m,d;
    scanf("%4d%2d%2d",&y,&m,&d);
    scanf("%4d%2d%2d",&yy,&mm,&dd);
    
    for(int i=1;i<13;i++){
     
        for(int j=0;j<=day[i];j++){
     
            // 0131 ---> 1310
            int year  = j%10*1000+j/10*100+i%10*10+i/10;
            if(year>=y && year<=yy) ans++;
        }
    }
    cout<<ans<<endl;
}

3.校门外的树

链接
题目大意：在0-N的区间都是树，现在要移除一些区间，求剩余树的个数，直接数轴模拟即可

#include
using namespace std;
const int maxn = 105;
int N,M,ans;
struct node{
     
    int L,R;
}x[maxn];
bool cmp(struct node a , struct node b){
     
    if(a.L!=b.L) return a.L<b.L;
    return a.R<b.R;
}
int main(){
     
    cin>>N>>M;
    for(int i=0;i<M;i++){
     
        cin>>x[i].L>>x[i].R;
    }
    sort(x,x+M,cmp);
    
    for(int i=0;i<M;i++){
     
        if(i==0) {
     ans = ans+(x[i].R-x[i].L+1) ;continue;}
        if(x[i].L<=x[i-1].R){
     
            if(x[i].R<=x[i-1].R){
     
                x[i].R = x[i-1].R;
                 continue;
            }
            ans = ans+(x[i].R - x[i-1].R);   //x[i].L这个点已经减去了，不用+1
        }else ans = ans+(x[i].R - x[i].L+1);
    }
    cout<<(N+1)-ans<<endl;
    /*
500 3
0 300
100 200
300 500
*/
}

4.数学考试

链接
题目大意就是n个题目，选取2k个题，并且获得的分数尽可能的大，他准备选2个不连续的长度为k的区间,即[L,L+1,L+2,…,L+k-1]，[R,R+1,R+2,…,R+k-1]（R >= L+k），由于两段之间是不连续的，但是每段里面的分数是连续的，我们可以用一个数组维护前i个分数之和，然后贪心，取得最大的分数，

#include
using namespace std;
const int maxn = 2e5+5;
const long long Max = 1e18;
long long  a[maxn];
int main(){
     
    int t;
    cin>>t;
    while(t--){
     
        memset(a,0,sizeof(a));
        int n,k;
        cin>>n>>k;
        for(int i=1;i<=n;i++){
     
            cin>>a[i];
            a[i] = a[i]+a[i-1];
        }
        long long  l = -Max , r = -Max;
        for(int i=k;i+k<=n;i++){
     
            l = max(l , a[i]-a[i-k]);
            r = max(r , l+a[i+k]-a[i]);
        }
        cout<<r<<endl;
    }
    
}

5.Subsequence

链接
题目大意：给定长度为n的整数数列以及整数S，求出总和不小于S的连续子串的长度的最小值，如果解不存在，输出0。直接用一个数组维护前缀和，然后得出解

#include
using namespace std;
typedef long long ll;
int T,n,x;
ll s;
int solve(){
     
    int ans = 0x3f3f3f3f,f=0;
    ll sum[100010]={
     0};   //前缀和 
    for(int i=1;i<=n;i++){
     
        cin>>x;
        sum[i] = sum[i-1]+x;
        if(sum[i]>s) f=1;
        if(x>s) ans = 1;
    }
    if(ans==1) return ans;  //存在一个数字直接大于S
    if(f==0) return 0;      //所有数字和都小于S
    
    for(int i=0,r=1;r<=n;){
     
        if(sum[r]-sum[i]<s) r++;  
        else {
     
            ans=min(ans,r-i);    //得到最小的区间
            i++;
        }
    }
    return ans;
}
int main(){
     
    cin>>T;
    while(T--){
     
        cin>>n>>s;
        cout<<solve()<<endl;
    }
}

6.字符串

链接
题目大意：给出字符串 S ， 问最短的 一个子串包含 26 个字母的子串的长度
用尺取法，一个游标记录区间的开始，一个记录区间的末尾，每次读取 r 右移，左边的出现过则 l 右移，如果cnt为26，更新答案

#include
using namespace std;
int vis[27];
int ans=0x3f3f3f3f , cnt, l ;
int main(){
     
    string s;
    cin>>s;
    for(int r=0;r<s.length();r++){
     
        if(!vis[s[r]-'a']) cnt++;  
        vis[s[r]-'a']++;
        
        while(vis[s[l]-'a']>1){
     
            vis[s[l]-'a']--;
            l++;
        }
        if(cnt==26) ans = min(ans , r-l+1);
    }
    cout<<ans<<endl;
}

7.丢手绢

链接
题目大意就是n个小朋友围城一个圈圈，求任意两个小朋友之间最远的距离，距离可以是逆时针也可以是顺时针，方法其实也是一样尺取法，模拟可以发现，两个小朋友之间的距离先是越来越远然后超过总距离一半的时候越来越近

#include
using namespace std;
const int maxn = 1e5+5;
int main()
{
     
    int n,a[maxn],totalLen = 0;
    cin>>n;
    for(int i = 0 ; i < n; i++)
    {
     
        scanf("%d",&a[i]);
        totalLen += a[i];    //总距离
    }
    int maxLen = 0;
    int curLen = 0;
    int index = 0;
    for(int i = 0; i < n ; i++)
    {
     
        while(curLen<totalLen/2)
        {
     
            curLen += a[index];  
            index ++;
            index %= n;
            if(curLen<=totalLen/2) maxLen = max(maxLen,curLen);
        }
        curLen -= a[i];
    }
    cout<<maxLen<<endl;
    return 0;
}

8.拼数

链接
题目大意就是给你n个正整数，拼成一个数，使其最大，直接模拟，贪心即可…

#include
using namespace std;
string a[25];
bool cmp(string a , string b){
     
    return a+b>b+a;
}
int n;
int main(){
     
    cin>>n;
    for(int i=0;i<n;i++) cin>>a[i];
    sort(a,a+n,cmp);
    for(int i=0;i<n;i++) cout<<a[i];
    cout<<endl;
}

9.纪念品分组

链接
题目大意就是n个物品分组，每组最多两件，并且两件之和不能超过一个值，简单的贪心就好了

// 20 20 30 50 60 70 80 90 90
#include
using namespace std;
const int maxn = 30000+3;
int w,n , a[maxn],ans;
int main(){
     
    cin>>w>>n;
    for(int i=0;i<n;i++) cin>>a[i];
    sort(a,a+n);
    int l = 0 , r=n-1;
    while(l<=r){
     
        if(a[l]+a[r]<=w) l++,r--;
        else r--;
        ans++;
    }
    cout<<ans<<endl;
}

10.国王的游戏

链接
题目意思就是n个人与国王站在一排，国王永远站在第一个，然后每个人的左右手有一个数，每个人得到国王赏赐的金币是排在自己之前的所有人的左手乘积除以自己右数的数，要是的得到最大奖励最少，由于数据很大，所以就用java写，不需要考虑精度问题，此题也是一个贪心，贪心的策略，羽巨已经推理过了，这边就直接上代码吧

import java.math.BigInteger;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
class H
{
     
	int l;
	int r;
}
class cmp implements Comparator<H>
{
     
	public int compare(H x,H y)
	{
     
		return x.l*x.r-y.l*y.r;
	}
}

public class Main 
{
     
	public static void main(String[] args) 
	{
     
		int a,b;   //国王
		Scanner in=new Scanner(System.in);
		int n=in.nextInt();
		a=in.nextInt();
		b=in.nextInt();
        
		H person[]=new H[1003];
		int i;
		for(i=1;i<=n;i++) 
		{
     
			person[i]=new H();
			person[i].l=in.nextInt();
			person[i].r=in.nextInt();
		}
        //排序
		Arrays.sort(person,1,n+1,new cmp());
        
		BigInteger ans=new BigInteger("0");
		BigInteger now=BigInteger.valueOf(a);
		for(i=1;i<=n;i++)
		{
     
			ans=ans.max(now.divide(BigInteger.valueOf(person[i].r)));
			now=now.multiply(BigInteger.valueOf(person[i].l));
		}
		System.out.println(ans);
	}
}

11.铺地毯

链接
题目大意就是如题目字面意思…贪心即可，按照面积小的放前面，大的放后面，然后输出最后覆盖那个点的那块布…

#include
using namespace std;
const int maxn = 1e4+4;
int n ,x,y;
struct node {
     
    int id,a,b,g,k;
    int eara;
}bu[maxn];
bool cmp(struct node a , struct node b){
     
    return a.eara<b.eara;
}
int main(){
     
    cin>>n;
    for(int i=0;i<n;i++){
     
        cin>>bu[i].a>>bu[i].b>>bu[i].g>>bu[i].k;
        bu[i].eara = bu[i].g*bu[i].k;
        bu[i].id = i+1;
    }
    cin>>x>>y;
    sort(bu,bu+n,cmp);
    //for(int i=0;i
    int f = -1;
    for(int i=n-1;i>=0;i--){
     
        if(bu[i].a<=x&&bu[i].b<=y && bu[i].a+bu[i].g>=x && bu[i].b+bu[i].k>=y){
     
            f = bu[i].id;
            break;
        }
    }
    cout<<f<<endl;
    
}

12.「土」巨石滚滚

链接
题目大意就如字面意思，按照人类本能贪心的思想，我们会先消除那种比自己小的ai能获取最大的bi，这样会使得m最大才能去消除其他的障碍物，即：
先用完所有加稳定性的，同时在此优先选择ai小的
然后考虑所有减稳定性的，同时优先选择减稳定性中ai大的

#include
using namespace std;
const int maxn = 5e5+5;
typedef long long ll;
ll n,m;
struct node{
     
    ll a,b;
    bool operator <(const node &x)
    {
     
        if(b-a>=0&&x.b-x.a>=0)    return a<x.a;
        if(b-a>=0)   return 1;
        if(x.b-x.a>=0)   return 0;
        return b>x.b;
    }
}x[maxn];


int main(){
     
    int t;
    cin>>t;
    while(t--){
     
        cin>>n>>m;
        for(int i=0;i<n;i++){
     
            cin>>x[i].a>>x[i].b;
        }
        sort(x , x+n);
        for(int i=0;i<n;i++) cout<<x[i].a<<" "<<x[i].b<<endl;
        int i=0,f = 1;
        for(i=0;i<n;i++){
     
            m = m-x[i].a;
            if(m<0) {
     f = 0 ; break;}
            m = m+x[i].b;
        }
        if(f)puts("Yes");
        else puts("No");
    }
}

13.Protecting the Flowers

链接
题目大意就是农夫有n头牛在吃花，农夫要把牛送回牛舍，所花的时间分别为TI，每头牛留在花园的吃花量分别为DI，花田上的花最少破坏的数量，
雨巨思想，三式大于一式，排序贪心即可。

// ta / da < tb / db
// ta * db < da*tb
#include
using namespace std;
typedef long long ll;
struct node
{
     
	ll d,t;
}a[100010];
ll res,n,s;
int cmp(node a,node b)
{
     
	return a.t*b.d<b.t*a.d;
}
int main()
{
     
	cin>>n;
	for(int i=1;i<=n;i++)	cin>>a[i].t>>a[i].d;
	sort(a+1,a+1+n,cmp);
	for(int i=1;i<=n;i++)
	{
     
		res+=s*a[i].d;   //第一头牛没得吃，直接被抬走了
		s+=a[i].t*2;
	}
	cout<<res<<endl;
	return 0;
}

14.毒瘤xor

链接
题目大意，就是选取一个x然后对一区间所有数亦或和，使其最大，
前缀和 + 位运算 + 贪心 ，具体如下

#include
using namespace std;
typedef long long ll;
const int maxn = 1e5+5;
int sum[maxn][32];    //维护前i个数字每一位有多少1
int main(){
     
    int n , data , q , l , r;
    cin>>n;
    for(int i=1;i<=n;i++){
     
        cin>>data;
        for(int j=0;j<31;j++){
     
            sum[i][j] = sum[i-1][j]+((data)>>j&1);
        }
    }
    cin>>q;
    while(q--){
     
        ll ans = 0;
        cin>>l>>r;
        for(int j=0;j<31;j++){
     
            int cnt = sum[r][j] - sum[l-1][j];   //区间数第j位1的个数
            int len = r-l+1;    //总个数
            //使区间和亦或最大，那么如果0多，我们更希望变为1，如果1多我们更希望不变
            // 0^1 = 1  1^1 = 0
            if(cnt < len-cnt) ans = ans+(1<<j);
        }
        cout<<ans<<endl;
    }
}

15.奇♂妙拆分

链接
将一个数能被拆分成多少个不同的自然数，使得这些自然数相乘的值等于被拆分的数。

#include
using namespace std;
int main()
{
     
    int t, ans,x;
    cin >> t;
    while(t--)
    {
     
        cin >> x;
        if (x == 1) cout << "1" << endl;
        else{
     
            ans = 2;
            for (int i=2;i*i<x;i++){
     
            // 9 16 25 所以小于即可
                if(x%i==0)ans++,x/=i;
            }
            cout << ans << endl;
        }
    }
}

16.Quasi Binary

链接
题目大意就是给你一个数n，分解为x个数，每个数只能由0和1组成，并且x个数相加等于n
例如：123 = 111+11+1

#include
using namespace std;
int ans[10], len ,x;
int main()
{
     
    cin>>x;
    for (int i = 1; i <= x; i *= 10) {
     
        int temp = x / i % 10;
        len = max(len, temp);
        for (int j = 1; j <= temp; ++j) ans[j] += i;
    }
    printf ("%d\n", len);
    for (int i = 1; i <= len; ++i) printf("%d\n", ans[i]);
    puts("");
}

17.「土」秘法地震

链接
题目意思如字面意思…前缀和+容斥的思想

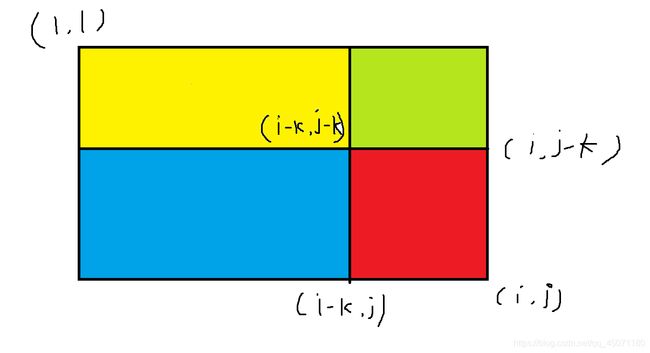
如果我们要算红色区域，那么就是 s[i][j] - s[i-k][j]-s[i][j-k] + s[i-k][j-k]
因为黄色区域减去了两次，所以要加回来一次。如果此区域有建筑物，则ans+1

#include
using namespace std;
const int N = 1010;
int n,m,k,s[N][N],ans;
char ch;
int main()
{
     
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
     
			cin>>ch;
			s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+ch-'0';
		}
/*
1 1 1 1 
1 2 2 2 
1 2 2 2 
1 2 2 3 
*/
    
	for(int i=k;i<=n;i++)
		for(int j=k;j<=m;j++)
		{
     
			if(s[i][j]-s[i-k][j]-s[i][j-k]+s[i-k][j-k]>0)
				ans++;
		}
    
	cout<<ans<<endl;
	return 0;
}