论文基于关键点预测网络提出CenterNet算法,将检测目标视为关键点,先找到目标的中心点,然后回归其尺寸。对比上一篇同名的CenterNet算法,本文的算法更简洁且性能足够强大,不需要NMS等后处理方法,能够拓展到其它检测任务中
来源:晓飞的算法工程笔记 公众号
论文: Objects as Points
Introduction
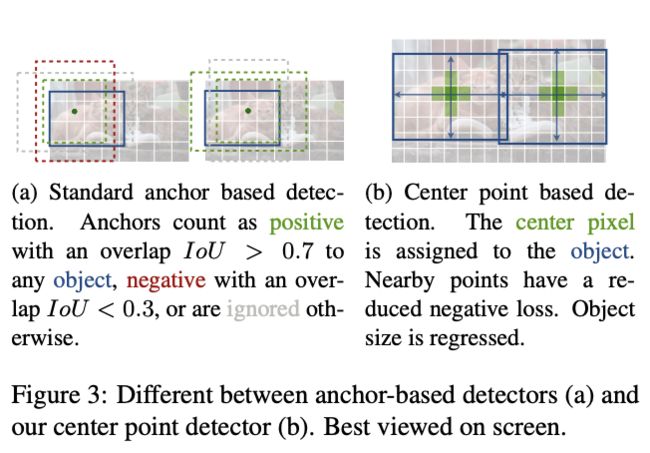
论文认为当前的anchor-based方法虽然性能很高,但需要枚举所有目标可能出现的位置以及尺寸,实际上是很浪费的。为此,论文提出了简单且高效的CenterNet,将目标表示为其中心点,再通过中心点特征回归目标的尺寸。
CenterNet将输入的图片转换成热图,热图中的高峰点对应目标的中心,将高峰点的特征向量用于预测目标的高和宽,如图2所示。在推理时,只需要简单的前向计算即可,不需要NMS等后处理操作。
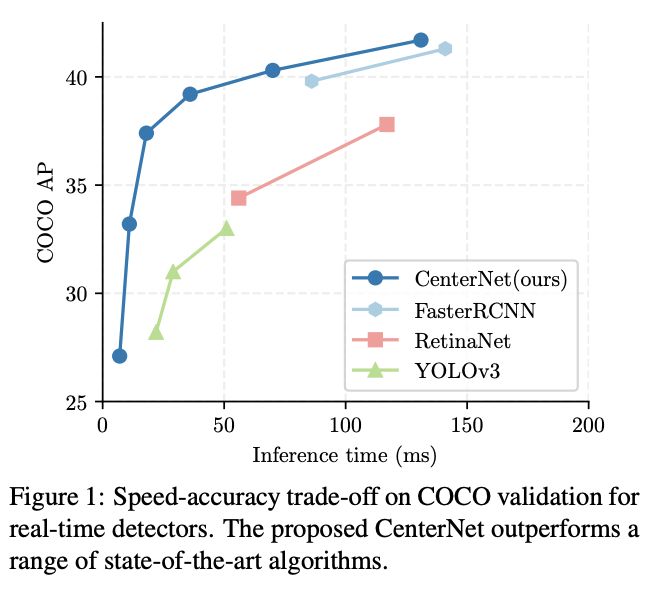
对比现有的方法,CenterNet在准确率和速度上有更好的trade-off。另外,CenterNet的架构是通用的,能够拓展到其它任务,比如3D目标检测以及人体关键点预测。
Preliminary
定义输入图片$I\in R^{W\times H\times 3}$,预测关键点热图$hat{Y}in
[ 0, 1 ]^{frac{W}{R}times frac{H}{R}times C}$,其中$R$为热图的缩放比例,设定为4,$C$为关键点的类型。当$hat{Y}_{x,y,c}=1$时,像素点为检测的关键点,当$hat{Y}_{x,y,c}=0$时,像素点为背景。在主干网络方法,论文尝试了多种全卷积encoder-decoder网络:Hourglass网络,带反卷积的残差网络以及DLA(deep layer aggregation)。
关键点预测部分的训练跟CornerNet一样,对于类别$c$的GT关键点$p\in \mathcal{R}^2$,计算其在热图上对应的位置$\tilde{p}=\lfloor\frac{p}{R}\rfloor$,然后使用高斯核$Y_{xyc}=exp(-\frac{(x-\tilde{p}_x)^2+(y-\tilde{p}_y)^2}{2\sigma^2_p })$将GT关键点散射,即根据像素位置到关键点的距离赋予不同的权值,得到GT热图$Y\in [ 0,1 ]^{(\frac{W}{R}\times \frac{H}{R}\times C)}$,$\sigma_p$为目标尺寸自适应的标准差,如图3所示。如果相同类别的高斯核散射重叠了,则取element-wise的最大值。训练的损失函数为惩罚衰减的逻辑回归,附加了focal loss:
$\alpha$和$\beta$为focal loss的超参数,$N$为关键点数。为了恢复特征图缩放带来的误差,额外预测每个关键点的偏移值$\hat{O}\in \mathcal{R}^{\frac{W}{R}\times \frac{H}{R}\times 2}$,偏移值与类别无关,通过L1损失进行训练:
偏移值只使用GT关键点,其它位置的点不参与训练。
Objects as Points
定义$(x^{(k)}_1, y^{(k)}_1, x^{(k)}_2,y^{(k)}_2)$为目标$k$的GT框,类别为$c_k$,其中心点为$p_k=(\frac{x^{(k)}_1+x^{(k)}_2}{2}, \frac{y^{(k)}_1+y^{(k)}_2}{2})$。论文使用热图$\hat{Y}$得到所有的中心点,另外再回归每个目标$k$的尺寸$s_k=(x^{(k)}_{2}-x^{(k)}_{1}, y^{(k)}_{2}-y^{(k)}_{1})$。为减少计算负担,尺寸的预测与类别无关$\hat{S}\in \mathcal{R}^{\frac{W}{R}\times \frac{H}{R}\times 2}$,通过L1损失进行训练,只使用GT关键点:
完整的CenterNet损失函数为:
CenterNet直接预测关键点热图$\hat{Y}$、偏移值$\hat{O}$和目标尺寸$\hat{S}$,每个位置共计预测$C+4$个输出。所有的输出共用主干网络特征,再接各自的$3\times 3$卷积、ReLU和$1\times 1$卷积。
在推理时,首先获取各类别热图上的高峰点,高峰点的值需高于周围八个联通点的值,最后取top-100高峰点。对于每个高峰点$(x_i, y_i)$,使用预测的关键点值$\hat{Y}_{x,y,c}$作为检测置信度,结合预测的偏移值$\hat{O}=(\delta \hat{x}_i, \delta \hat{y}_i)$和目标尺寸$\hat{S}=(\hat{w}_i, \hat{h}_i)$生成预测框:
由于高峰点的提取方法足以替代NMS的作用,所有的预测框都直接通过关键点输出,不需要再进行NMS操作以及其它后处理。需要注意的是,论文采用了巧妙的方法实现高峰点获取,先对特征图使用padding=1的$3\times 3$最大值池化,然后对比输出特征图和原图,值一样的点即为满足要求的高峰点。
Implementation details
CenterNet的输入为$512\times 512$,输出的热图大小为$128\times 128$。实验测试了4种网络结构:ResNet-18、ResNet-101、DLA-34和Hourglass-104,其中使用可变形卷积对ResNet和DLA-34进行了改进。
Hourglass
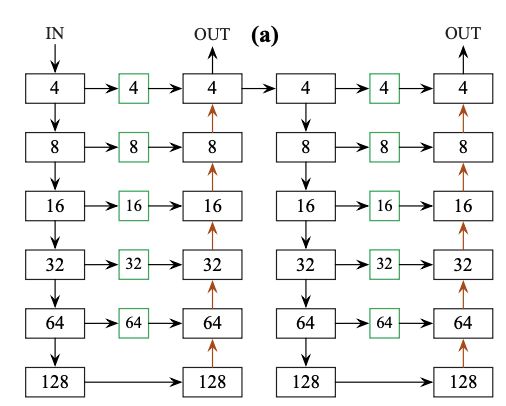
Hourglass结构如图a所示,框中的数字为特征图的缩放比例,包含两个hourglass模块,每个模块有5个下采样层以及5个上采样层,上采样和下采样对应的层有短路连接。Hourglass的网络尺寸最大,关键点预测的效果也是最好的。
ResNet
ResNet大体结构跟原版一致,加入了反卷积用来恢复特征图大小,反卷积的权值初始化为双线性插值操作,虚线箭头为$3\times 3$可变形卷积操作。
DLA
DLA使用层级短路连接,原版的结构如图c所示。论文将大部分的卷积操作修改为可变形卷积,并对每层的输出进行了$3\times 3$卷积融合,最后使用$1\times 1$卷积输出到目标维度,如图d所示。
Experiment
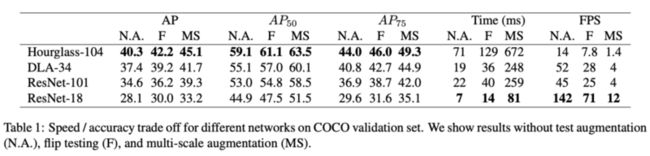
不同主干网络在目标检测上的准确率和速度对比。
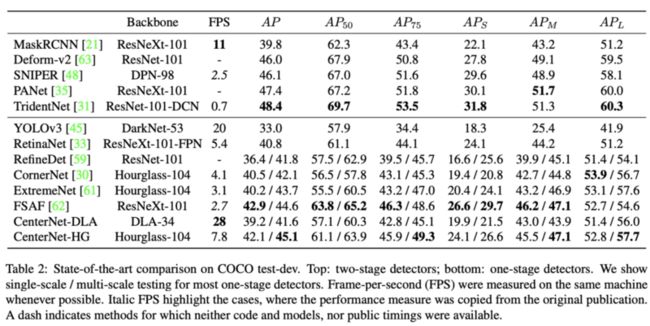
目标检测性能对比。
3D检测性能对比。
人体关键点检测性能对比。
Conclusion
论文基于关键点预测网络提出CenterNet算法,将检测目标视为关键点,先找到目标的中心点,然后回归其尺寸。对比上一篇同名的CenterNet算法,本文的算法更简洁且性能足够强大,不需要NMS等后处理方法,能够拓展到其它检测任务中 。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
![]()