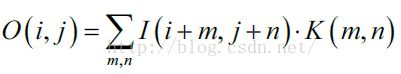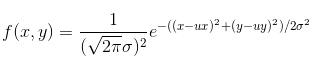CV笔记4：图像噪声及图像平滑(基于python-opencv实现)

目录

一、图像噪声介绍

1.1 高斯噪声

1.2 椒盐噪声

二、图像滤波

三、图像平滑（降噪）

3.1 均值滤波（方框滤波的特殊情况）

3.2 高斯滤波

3.3 中值滤波

3.4 双边滤波

参考

---

一、图像噪声介绍

图像噪声（image noise）是图像颜色的随机变化，是被拍摄的物体本身没有的颜色变化，是多余的干扰信息。

噪声产生的原因：

• 图像获取过程：数码相机的传感器和电路、不规范的操作
• 图像信号传输过程：传输介质和记录设备的缺陷

1.1 高斯噪声

高斯噪声指概率密度函数服从高斯分布（即正态分布）的一类噪声。

1.2 椒盐噪声

椒盐噪声，是随机出现的白点或者黑点（盐是白色而黑胡椒是黑色）

如上图，椒盐噪声在白色区域多呈现黑色噪点，在黑色区域多呈现白色噪点。

二、图像滤波

图像滤波既可以在实域进行，也可以在频域进行。图像滤波可以更改或者增强图像。通过滤波，可以强调一些特征或者去除图像中一些不需要的部分。滤波是一个邻域操作算子，利用给定像素周围的像素的值决定此像素的最终的输出值。

图像滤波可以通过公式：

进行计算，其中K为滤波器，在很多文献中也称之为核（kernel）。常见的应用包括降噪、图像增强、检测边缘、检测角点、模板匹配等。

图像滤波分类如下：

线性滤波： 对邻域中的像素的计算为线性运算时，如利用窗口函数进行平滑加权求和的运算，或者某种卷积运算，都可以称为线性滤波。常见的线性滤波有：均值滤波、高斯滤波、盒子滤波、拉普拉斯滤波等等，通常线性滤波器之间只是模版系数不同。

非线性滤波： 非线性滤波利用原始图像跟模版之间的一种逻辑关系得到结果，如最值滤波器，中值滤波器。比较常用的有中值滤波器和双边滤波器。

在opencv中，提供了一个函数cv.filter2D()来将内核与图像进行卷积，从而实现图像的滤波计算。

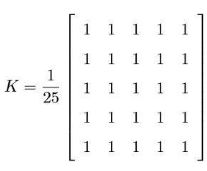
举例：下面是一个5X5的平均滤波器核：

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('image.jpg')
kernel = np.ones((5, 5), dtype='f4')/25

# when ddepth=-1, the output image will have the same depth as the source.
dst = cv2.filter2D(img, ddepth=-1, kernel=kernel)

# show image
plt.figure('filter image')
plt.subplot(121), plt.imshow(img[:, :, ::-1]), plt.title('original image')
plt.subplot(122), plt.imshow(dst[:, :, ::-1]), plt.title('filter image')
plt.show()

效果：

三、图像平滑（降噪）

通过将图像与低通滤波器内核进行卷积来实现图像模糊。这对于消除噪音很有用。它实际上从图像中消除了高频部分（例如噪声，边缘）。因此，在此操作中边缘有些模糊。（有一些模糊技术也可以不模糊边缘）。OpenCV主要提供四种类型的模糊技术：均值滤波、高斯滤波、中值滤波和双边滤波。

3.1 均值滤波（方框滤波的特殊情况）

均值滤波（normalized box filter）：用其像素点周围像素的平均值代替元像素值，在滤除噪声的同时也会滤掉图像的边缘信息。根据冈萨雷斯书中的描述，均值模糊可以模糊图像以便得到感兴趣物体的粗略描述，也就是说，去除图像中的不相关细节，其中“不相关”是指与滤波器模板尺寸相比较小的像素区域，从而对图像有一个整体的认知。即为了对感兴趣的物体得到一个大致的整体的描述而模糊一幅图像，忽略细小的细节。均值滤波本身存在着固有的缺陷，即它不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变得模糊，不能很好地去除噪声点。特别是椒盐噪声。

均值滤波模板公式表示如下：

g(x,y)为该邻域的中心像素，n跟系数模版大小有关，模板是可变的，一般取奇数，如5 * 5 , 7 * 7等等。亦如下公式所示：

在opencv中，可以使用cv2.blur()和cv2.boxFilter()来实现均值滤波。其中调用blur()等效于调用将normalize=true的boxFilter()。box filter即方框（盒子）滤波，是一种非常有用的线性滤波，均值滤波就是盒子滤波归一化的特殊情况。

方框滤波在原理上，是采用如下公式中的一个卷积核与图像进行卷积：

式中：

可见，归一化了就是均值滤波；不归一化则可以计算每个像素邻域上的各种积分特性，方差、协方差，平方和等等。

举例：仍然使用5*5的均值滤波核

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('image.jpg')

dst = cv2.boxFilter(img, -1, (5, 5), normalize=True) # box filter, normalized
dst1 = cv2.blur(img, (5, 5))  # blurred image

plt.figure('blurred image')
plt.subplot(131), plt.imshow(img[:, :, ::-1]), plt.title('original')
plt.subplot(132), plt.imshow(dst[:, :, ::-1]), plt.title('box filter normalized')
plt.subplot(133), plt.imshow(dst1[:, :, ::-1]), plt.title('blurred')
plt.show()

效果：

3.2 高斯滤波

高斯滤波是一种线性平滑滤波器，对于服从正态分布的噪声有很好的抑制作用。在实际场景中，我们通常会假定图像包含的噪声为高斯白噪声，所以在许多实际应用的预处理部分，都会采用高斯滤波抑制噪声，如传统车牌识别等。

高斯滤波和均值滤波一样，都是利用一个掩膜和图像进行卷积求解。不同之处在于：均值滤波器的模板系数都是相同的为1，而高斯滤波器的模板系数，则随着距离模板中心的增大而系数减小（服从二维高斯分布）。所以，高斯滤波器相比于均值滤波器对图像个模糊程度较小，更能够保持图像的整体细节。

二维高斯分布如下：

我们不必纠结于系数，因为它只是一个常数！并不会影响互相之间的比例关系，并且最终都要进行归一化，所以在实际计算时我们是忽略它而只计算后半部分:

其中(x,y)为掩膜内任一点的坐标，(ux,uy)为掩膜内中心点的坐标，在图像处理中可认为是整数；σ是标准差。因此，只要知道模板的大小和高斯函数的方差,由二维高斯函数的表达式很容易计算出高斯核，只要在归一化就可以了。

这样计算出来的模板有两种形式：小数和整数。

• 小数形式的模板，就是直接计算得到的值，没有经过任何的处理；
• 整数形式的，则需要进行归一化处理，将模板左上角的值归一化为1。使用整数的模板时，需要在模板的前面加一个系数，系数为模板系数和的倒数。

对于方差σ来说，代表着数据的离散程度，如果σ较小，那么生成的模板的中心系数较大，而周围的系数较小，这样对图像的平滑效果就不是很明显；反之，σ较大，则生成的模板的各个系数相差就不是很大，比较类似均值模板，对图像的平滑效果比较明显。

来看下一维高斯分布的概率分布密度图：

于是我们有如下结论：σ越小分布越瘦高，σ越大分布越矮胖。

• σ越大，分布越分散，各部分比重差别不大，于是生成的模板各元素值差别不大，类似于平均模板；
• σ越小，分布越集中，中间部分所占比重远远高于其他部分，反映到高斯模板上就是中心元素值远远大于其他元素值，于是自然而然就相当于中间值得点运算。

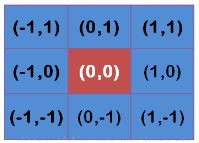
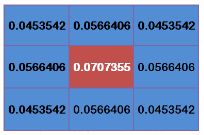
例如：要产生一个3×3的高斯滤波器模板，以模板的中心位置为坐标原点进行取样。模板在各个位置的坐标，如下所示（x轴水平向右，y轴竖直向下）。

 

将这模板中的坐标x,y代入到二维高斯函数中，假定均值为0，σ为1.5,得到模糊半径为1的权重矩阵如下:

这9个点的权重总和等于0.4787147，如果要计算这9个点的加权平均，还必须让它们的权重之和等于1，因此上面9个值还要分别除以0.4787147，得到最终的权重矩阵：

我们可以在opencv中使用cv2.GaussianBlur()进行高斯滤波，需要指定高斯核的宽和高（必须是奇数），以及高斯函数沿X,Y方向的标准差。如果我们只指定了X方向的标准差，Y方向也会取相同值，如果两个标准差都是0.那么函数会根据核函数的大小自己计算。

# 0是指根据窗口大小（5,5）来计算高斯函数标准差 
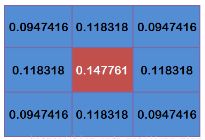
blur = cv2.GaussianBlur(img,(5,5),0)

在opencv中，我们还可以使用cv2.getGaussianKernel()自己构建一个高斯核，使用该函数我们只能得到一维的高斯核，可以使用下面的方法得到二维高斯核：

kernel_x = cv2.getGaussianKernel(3, 1.5)  # para1:kernel size, para2:sigma
kernel_y = cv2.getGaussianKernel(3, 1.5)
gaussian_kernel = kernel_x * kernel_y.T

# result
[[0.09474166 0.11831801 0.09474166]
 [0.11831801 0.14776132 0.11831801]
 [0.09474166 0.11831801 0.09474166]]

举例：使用5*5的高斯核进行图像平滑

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('image.jpg')

# gaussian blur
dst = cv2.GaussianBlur(img, (5, 5), 0) # para1:img,  para2:kernel size, para3:sigma

plt.figure('gaussian blur')
plt.subplot(121), plt.imshow(img[:, :, ::-1]), plt.title('original')
plt.subplot(122), plt.imshow(dst[:, :, ::-1]), plt.title('gaussian blur')
plt.show()

效果：

3.3 中值滤波

中值滤波是一种典型的非线性滤波，是基于排序统计理论的一种能够有效抑制噪声的非线性信号处理技术，基本思想是用像素点邻域灰度值的中值来代替该像素点的灰度值，让周围的像素值接近真实的值从而消除孤立的噪声点。该方法在去除脉冲噪声、椒盐噪声的同时能保留图像的边缘细节。这些优良特性是线性滤波所不具备的。

在opencv中使用cv2.medianBlur()函数进行中值滤波。

举例：使用3*3的中值滤波模板进行中值滤波

import cv2
import matplot.pyplot as plt

img_pcb = cv2.imread('pcb.jpg')

dst = cv2.medianBlur(img_pcb, 3)  # para1:image, para2:kernel size(int)

plt.figure('median blur')
plt.subplot(121), plt.imshow(img_pcb), plt.title('original')
plt.subplot(122), plt.imshow(dst), plt.title('median blur')
plt.show()

效果：

3.4 双边滤波

双边滤波（Bilateral filter）是一种非线性的滤波方法，是结合图像的空间邻近度和像素值相似度的一种折衷处理，同时考虑空域信息和灰度相似性，达到保边去噪的目的。具有简单、非迭代、局部的特点。双边滤波器的好处是可以做边缘保存（edge preserving），一般过去用的维纳滤波或者高斯滤波去降噪，都会较明显地模糊边缘，对于高频细节的保护效果并不明显。

下面的这张图解释了高斯模板导致边缘模糊的原因：平坦区域正常滤波，图像细节没有变化，而在突变的边缘上，因为只使用了距离来确定的滤波权重，导致边缘被模糊。

双边滤波基于高斯滤波的思想，在高斯滤波的基础上，加上图像像素值对中心像素的影响，两者共同影响中心像素的值。所以在边缘附近，离的较远的像素不会太多影响到边缘上的像素值，这样就保证了边缘附近像素值的保存。但是由于保存了过多的高频信息，对于彩色图像里的高频噪声，双边滤波器不能够干净的滤掉，只能够对于低频信息进行较好的滤波。双边滤波公式如下：

公式中Ip为原像素，Range Weight为像素范围域核，Space Weight为空间域核，1/Wp为归一化操作，BF[I]p为输出像素。

为了理解双边滤波的公式，先说明下面两个概念：空间距离和灰度距离

空间距离：当前点距离滤波模板中心点的欧式距离:

灰度距离：当前点距离滤波模板中心点的灰度的差值的绝对值:

双边滤波的核函数就是空间域核和像素范围域核的综合结果，即上图公式中的Space Weight和Range Weight两部分的结合，而空间域核就是采用空间距离公式进行计算，像素范围域核就是采用灰度距离公式进行计算的来的。通过公式我们可以看出：

• 1）在图像的平坦区域，像素值变化很小，那么像素差值接近于0，对应的像素范围域权重接近于1，此时空间域权重起主要作用，相当于进行高斯模糊；
• 2）在图像的边缘区域，像素值变化很大，那么像素差值大，对应的像素范围域权重变大，即使距离远空间域权重小，加上像素域权重总的系数也较大，从而保护了边缘的信息。

双边滤波的效果如下图，在突变的边缘上，使用了像素差权重，所以很好的保留了边缘。

双边滤波的原理如下图所示：

在opencv中，可以使用cv2.bilateralFilter()函数实现双边滤波。

举例：使用邻域直径为9，空间域方差和像素范围域方差均为75的双边滤波进行图像平滑

#cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace)
#d – Diameter of each pixel neighborhood that is used during filtering.
# If it is non-positive, it is computed from sigmaSpace 

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('image.jpg')

# 9 邻域直径，两个 75 分别是空间高斯函数标准差，灰度值相似性高斯函数标准差 
blur = cv2.bilateralFilter(img,9,75,75)

plt.figure('bilateral filter')
plt.subplot(121), plt.imshow(img), plt.title('original')
plt.subplot(122), plt.imshow(dst), plt.title('bilateral filter')
plt.show()

效果：

 

参考

计算机视觉、图像处理中常见的滤波操作

opencv中常用的线性滤波器--boxFilter(),blur(),GaussianBlur()

图像滤波算法总结

OpenCV实现二维高斯核GaussianKernel

图像平滑

双边滤波

双边滤波算法