强化学习(Reinforcement learning)综述
文章目录
- Reinforcement learning 综述
-
- 强化学习的分类
-
- 环境(Model-free,Model-based)
- Based(Policy-Based RL & Value-Based RL)
- 回合更新和单步更新
- 在线学习和离线学习
- 强化学习理论基础
-
- 马尔可夫决策过程(Markov Decision Processes,MDPs)
- 基本概念
- MDP 求解
- Bellman期望方程
-
- Bellman方程的分析
- 状态价值函数和动作价值函数的关系
- 最优方程
-
- 最优价值函数(optimal state-value function)
- Bellman最优方程
- 最优策略(Optimal Policy)
- 求解 Bellman 最优方程
- 动态规划求解 MDPs 的 Planning
-
- 1.Policy Iteration
- 2.Value Iteration
- 同步动态规划算法小结
- Model-free v.s. Model-based
- Q-learning
- State-Action-Reward-State-Action (SARSA)
- Deep Q Network(DQN)
-
- pytorch实现DQN
- Deep Deterministic Policy Gradient (DDPG)
- PG 和 Q learning 的问题
- 优势函数 Advantage Function
- Trust Region Policy Optimization (TRPO)
- Proximal Policy Optimization (PPO)
Reinforcement learning 综述
强化学习的分类
环境(Model-free,Model-based)
Model-free 的方法有很多, 像 Q learning, Sarsa, Policy Gradients 都是从环境中得到反馈然后从中学习. 而 model-based RL 只是多了一道程序, 为真实世界建模, 也可以说他们都是 model-free 的强化学习, 只是 model-based 多出了一个虚拟环境, 我们不仅可以像 model-free 那样在现实中玩耍,还能在游戏中玩耍, 而玩耍的方式也都是 model-free 中那些玩耍方式, 最终 model-based 还有一个杀手锏是 model-free 超级羡慕的. 那就是想象力。
Based(Policy-Based RL & Value-Based RL)
我们现在说的动作都是一个一个不连续的动作, 而对于选取连续的动作, 基于价值的方法是无能为力的. 我们却能用一个概率分布在连续动作中选取特定动作, 这也是基于概率的方法的优点之一. 那么这两类使用的方法又有哪些呢?基于概率这边, 有 Policy Gradients, 在基于价值这边有 Q learning, Sarsa 等. 而且我们还能结合这两类方法的优势之处, 创造更牛逼的一种方法, 叫做 Actor-Critic, actor 会基于概率做出动作, 而 critic 会对做出的动作给出动作的价值, 这样就在原有的 policy gradients 上加速了学习过程.
回合更新和单步更新
Monte-carlo learning 和基础版的 policy gradients 等 都是回合更新制, Qlearning, Sarsa, 升级版的 policy gradients 等都是单步更新制. 因为单步更新更有效率, 所以现在大多方法都是基于单步更新. 比如有的强化学习问题并不属于回合问题.
在线学习和离线学习
最典型的在线学习就是 Sarsa 了, 还有一种优化 Sarsa 的算法, 叫做 Sarsa lambda, 最典型的离线学习就是 Q learning, 后来人也根据离线学习的属性, 开发了更强大的算法, 比如让计算机学会玩电动的 Deep-Q-Network.
强化学习理论基础
马尔可夫决策过程(Markov Decision Processes,MDPs)
MDPs 简单说就是一个智能体(Agent)采取行动(Action)从而改变自己的状态(State)获得奖励(Reward)与环境(Environment)发生交互的循环过程。
MDP 的策略完全取决于当前状态(Only present matters),这也是它马尔可夫性质的体现。
其可以简单表示为 M = < S , A , P s , a , R > M =
基本概念
1. s ∈ S s \in S s∈S:有限状态state集合,s表示某个特定状态
2. a ∈ A a \in A a∈A:有限动作action集合,a表示某个特定动作
3.Transition Model T ( S , a , S ′ ) ∼ P τ ( s ′ ∣ s , a ) T(S,a,S') \sim P_\tau(s'|s,a) T(S,a,S′)∼Pτ(s′∣s,a): Transition Model, 根据当前状态 s 和动作 a 预测下一个状态 s’,这里的 P τ P_\tau Pτ表示从 s 采取行动 a 转移到 s’ 的概率
4.Reward R ( s , a ) = E [ R t + 1 ∣ s , a ] R(s,a)=E[R_{t+1}|s,a] R(s,a)=E[Rt+1∣s,a] :表示 agent 采取某个动作后的即时奖励,它还有 R ( s , a , s ’ ) R(s, a, s’) R(s,a,s’), R ( s ) R(s) R(s) 等表现形式,采用不同的形式,其意义略有不同
5.Policy π ( s ) → a \pi(s) \rightarrow a π(s)→a: 根据当前 state 来产生 action,可表现为 a = π ( s ) a=\pi(s) a=π(s) 或 π ( a ∣ s ) = P [ a ∣ s ] \pi(a|s)=P[a|s] π(a∣s)=P[a∣s],后者表示某种状态下执行某个动作的概率
回报(Return):
U ( s o s 1 s 2 . . . ) U(s_o s_1 s_2 ...) U(sos1s2...) 与 折扣率(discount) γ ∈ [ 0 , 1 ] \gamma \in [0,1] γ∈[0,1]: U U U 代表执行一组 action 后所有状态累计的 reward 之和,但由于直接的 reward 相加在无限时间序列中会导致无偏向,而且会产生状态的无限循环。因此在这个 Utility 函数里引入 γ \gamma γ 折扣率这一概念,令往后的状态所反馈回来的 reward 乘上这个 discount 系数,这样意味着当下的 reward 比未来反馈的 reward 更重要,这也比较符合直觉。定义
U ( s o s 1 s 2 . . . ) = ∑ t = 0 ∞ γ t R ( s t ) 0 ≤ γ < 1 ≤ ∑ t = 0 ∞ γ t R m a x = R m a x 1 − γ U(s_o s_1 s_2 ...) = \sum_{t=0}^\infty \gamma^tR(s_t) \quad 0 \leq \gamma<1 \\ \qquad \qquad \leq \sum_{t=0}^\infty \gamma^tR_{max}= {R_{max} \over {1-\gamma}} U(sos1s2...)=t=0∑∞γtR(st)0≤γ<1≤t=0∑∞γtRmax=1−γRmax
由于我们引入了 discount,可以看到我们把一个无限长度的问题转换成了一个拥有最大值上限的问题。
强化学习的目的是 最大化长期未来奖励,即寻找最大的 U。(注:回报也作 G 表示)
基于回报(return),我们再引入两个函数
状态价值函数: v ( s ) = E [ U t ∣ S t = s ] v(s) = E[U_t|S_t=s] v(s)=E[Ut∣St=s],意义为基于 t 时刻的状态 s 能获得的未来回报(return)的期望,加入动作选择策略后可表示为 v π ( s ) = E π [ U t ∣ S t = s ] v_{\pi}(s) = E_{\pi}[U_t|S_t=s] vπ(s)=Eπ[Ut∣St=s]( U t = R t + 1 + γ R t + 2 + . . . + γ T − t − 1 R T U_t = R_{t+1}+\gamma R_{t+2} + ... + \gamma ^{T-t-1} R_T Ut=Rt+1+γRt+2+...+γT−t−1RT)
动作价值函数: q π = E π [ U t ∣ S t = s , A t = a ] q_\pi = E_\pi[U_t|S_t=s,A_t=a] qπ=Eπ[Ut∣St=s,At=a],意义为基于 t 时刻的状态 s,选择一个 action 后能获得的未来回报(return)的期望。价值函数用来衡量某一状态或动作-状态的优劣,即对智能体来说是否值得选择某一状态或在某一状态下执行某一动作。
MDP 求解
我们需要找到最优的策略使未来回报最大化,求解过程大致可分为两步,具体内容会在后面展开
1.预测:给定策略,评估相应的状态价值函数和状态-动作价值函数
2.行动:根据价值函数得到当前状态对应的最优动作
Bellman期望方程
Bellman方程的分析
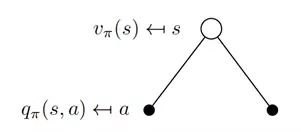
为了更加了解方程中期望的具体形式,可以见下图,第一层的空心圆代表当前状态(state),向下连接的实心圆代表当前状态可以执行两个动作,第三层代表执行完某个动作后可能到达的状态 s’。

根据上图得出状态价值函数公式:
v π ( s ) = E [ U t ∣ S t = s ] = ∑ a ∈ A π ( a ∣ s ) ( R s a + γ ∑ s ′ ∈ S P s s ′ a v π ( s ′ ) ) v_\pi(s)=E[U_t|S_t=s]= \sum_{a \in A}\pi(a|s)(R_s^a+\gamma\sum_{s' \in S}P_{ss'}^av_\pi(s')) vπ(s)=E[Ut∣St=s]=∑a∈Aπ(a∣s)(Rsa+γ∑s′∈SPss′avπ(s′))
其中, P s s ′ a = P ( S t + 1 = s ′ ∣ S t = s , A t = a ) P_{ss'}^a=P(S_{t+1}=s'|S_t=s,A_t=a) Pss′a=P(St+1=s′∣St=s,At=a)
上式中策略 π \pi π 是指给定状态 s 的情况下,动作 a 的概率分布,即 π ( a ∣ s ) = P ( a ∣ s ) \pi(a|s)=P(a|s) π(a∣s)=P(a∣s)
我们将概率和转换为期望,上式等价于:
v π ( s ) = E π [ R s a + γ v π ( S t + 1 ) ∣ S t = s ] v_\pi(s)=E_\pi[R_s^a+\gamma v_\pi(S_{t+1})|S_t=s] vπ(s)=Eπ[Rsa+γvπ(St+1)∣St=s]
同理,我们可以得到动作价值函数的公式如下:
q π ( s , a ) = E π [ R t + 1 + γ q π ( S t + 1 , A t + 1 ) ∣ S t = s , A t = a ] q_\pi(s,a)=E_\pi[R_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1})|S_t=s,A_t=a] qπ(s,a)=Eπ[Rt+1+γqπ(St+1,At+1)∣St=s,At=a]
如上图,Bellman 方程也可以表达成矩阵形式: v = R + γ P v v=R+\gamma Pv v=R+γPv,可直接求出 v = ( I − γ P ) − 1 R v=(I-\gamma P)^{-1}R v=(I−γP)−1R;其复杂度为 O ( n 3 ) O(n^3) O(n3),一般可通过动态规划、蒙特卡洛估计与 Temporal-Difference learning 求解。
状态价值函数和动作价值函数的关系
v π ( s ) = ∑ a ∈ A π ( a ∣ s ) q π ( s , a ) = E [ q π ( s , a ) ∣ S t = s ] q π ( s , a ) = R s a + γ ∑ s ′ ∈ S P s s ′ a ∑ a ′ ∈ A π ( a ′ ∣ s ′ ) q π ( s ′ ∣ a ′ ) = R s a + γ ∑ s ′ ∈ S P s s ′ a v π ( s ′ ) v_\pi(s) = \sum_{a \in A}\pi(a|s)q_\pi(s,a) = E[q_\pi(s,a)|S_t=s]\\ q_\pi(s,a) = R^a_s + \gamma \sum_{s' \in S}P_{ss'}^a \sum_{a' \in A}\pi(a'|s')q_\pi(s'|a') = R^a_s + \gamma \sum_{s' \in S} P_{ss'}^av_\pi(s') vπ(s)=a∈A∑π(a∣s)qπ(s,a)=E[qπ(s,a)∣St=s]qπ(s,a)=Rsa+γs′∈S∑Pss′aa′∈A∑π(a′∣s′)qπ(s′∣a′)=Rsa+γs′∈S∑Pss′avπ(s′)
最优方程
最优价值函数(optimal state-value function)
v ∗ ( s ) = max π v π ( s ) q ∗ ( s , a ) = max π q π ( s , a ) v_*(s)=\max_{\pi}{v_{\pi}(s)} \\ q_*(s,a) = \max_{\pi}q_{\pi}(s,a) v∗(s)=πmaxvπ(s)q∗(s,a)=πmaxqπ(s,a)
其意义为所有策略下价值函数的最大值
Bellman最优方程
v ∗ ( s ) = max a q ∗ ( s , a ) = max a ( R s a + γ ∑ s ′ ∈ S P s s ′ a v ∗ ( s ′ ) ) q ∗ ( s , a ) = R s a + γ ∑ s ′ ∈ S P s s ′ a v ∗ ( s ′ ) = R s a + γ ∑ s ’ ∈ S P s s ′ a max a ’ q ∗ ( s ′ , a ′ ) v_*(s)= \max_aq_*(s,a)= \max_a\left( R_s^a + \gamma\sum_{s'\in S}P_{ss'}^a v_*(s') \right) \\ q_*(s,a)= R_s^a+\gamma \sum_{s'\in S}P_{ss'}^av_*(s') = R_s^a + \gamma \sum_{s’ \in S}P_{ss'}^a\max_{a’}q_*(s',a') v∗(s)=amaxq∗(s,a)=amax(Rsa+γs′∈S∑Pss′av∗(s′))q∗(s,a)=Rsa+γs′∈S∑Pss′av∗(s′)=Rsa+γs’∈S∑Pss′aa’maxq∗(s′,a′)
- v 描述了处于一个状态的长期最优化价值,即在这个状态下考虑到所有可能发生的后续动作,并且 都挑选最优的动作来执行 的情况下,这个状态的价值
- q 描述了处于一个状态并执行某个动作后所带来的长期最优价值,即在这个状态下执行某一特定动作后,考虑 再之后所有可能处于的状态并且在这些状态下总是选取最优动作 来执行所带来的长期价值
最优策略(Optimal Policy)
关于收敛性:(对策略定义一个偏序)
π ≥ π ′ i f v π ( s ) ≥ v π ′ ( s ) , ∀ s \pi \ge \pi' \quad if\; v_{\pi}(s)\ge v_{\pi'}(s),\forall s π≥π′ifvπ(s)≥vπ′(s),∀s
定理:
对于任意 MDP:
-
总是存在一个最优策略 π ∗ \pi_* π∗,它比其它任何策略都要好,或者至少一样好
-
所有最优决策都达到最优值函数,
v π ∗ ( s ) = v ∗ ( s ) v_{\pi_*}(s)=v_*(s) vπ∗(s)=v∗(s) -
所有最优决策都达到最优行动值函数,
q π ∗ ( s , a ) = q ∗ ( s , a ) q_{\pi_*}(s,a)=q_*(s,a) qπ∗(s,a)=q∗(s,a)
最优策略可从最优状态价值函数或者最优动作价值函数得出:
π ∗ ( a ∣ s ) = { 1 , i f a = arg max a ∈ A q ∗ ( s , a ) 0 , o t h e r w i s e \pi_*(a|s) = \begin{cases} 1, & if\quad a = \arg\max_{a \in A} q_*(s,a)\\ 0, & otherwise \end{cases} π∗(a∣s)={ 1,0,ifa=argmaxa∈Aq∗(s,a)otherwise
求解 Bellman 最优方程
通过解 Bellman 最优性方程找一个最优策略需要以下条件:
- 动态模型已知
- 拥有足够的计算空间和时间
- 系统满足 Markov 特性
所以我们一般采用近似的办法,很多强化学习方法一般也是研究如何近似求解 Bellman 方程,一般有下面几种(后文会做具体讲解):
- Value Iteration
- Policy Iteration
- Q-learning
- Sarsa
MDPs 还有下面几种扩展形式:
- Infinite and continuous MDPs
- Partially observable MDPs
- Undiscounted, average reward MDPs
动态规划求解 MDPs 的 Planning
动态规划是一种通过把复杂问题划分为子问题,并对自问题进行求解,最后把子问题的解结合起来解决原问题的方法。「动态」是指问题由一系列的状态组成,而且状态能一步步地改变,「规划」即优化每一个子问题。因为MDP 的 Markov 特性,即某一时刻的子问题仅仅取决于上一时刻的子问题的 action,并且 Bellman 方程可以递归地切分子问题,所以我们可以采用动态规划来求解 Bellman 方程。
MDP 的问题主要分两类
- Prediction 问题
- 输入:MDP $ (S,A,P,R,\gamma) $ 和策略(policy)$ \pi $
- 输出:状态价值函数 v π v_\pi vπ
- Control 问题
- 输入:MDP $ (S,A,P,R,\gamma) $
- 输出:最优状态价值函数 v ∗ v_* v∗和最优策略 π \pi π
解决也是分两种,见下文
1.Policy Iteration
步骤:
- Iterative Policy Evaluation:
- 基于当前的 Policy 计算出每个状态的 Value function
- 同步更新:每次迭代更新所有的状态的 v
V k + 1 ( s ) = ∑ a ∈ A π ( a ∣ s ) ( R s a + γ ∑ s ′ ∈ S P s s ′ a v k ( s ′ ) ) V_{k+1}(s)=\sum_{a\in A}\pi(a|s)\left( R_s^a+\gamma\sum_{s'\in S}P_{ss'}^av_k(s')\right) Vk+1(s)=a∈A∑π(a∣s)(Rsa+γs′∈S∑Pss′avk(s′))
- 矩阵形式: v k + 1 = R π + γ P π v k \mathbf{v^{k+1}=R^{\pi}+\gamma P^{\pi}v^k} vk+1=Rπ+γPπvk
- 左边是第 k 次迭代每个 state 上状态价值函数的值,右边是通过贪心(greedy)算法找到策略
- 计算实例:
- k=2, -1.7 ≈ \approx ≈ -1.75 = 0.25*(-1+0) + 0.25*(-1-1) + 0.25*(-1-1) + 0.25*(-1-1)
- k=3, -2.9 ≈ \approx ≈ -2.925 = 0.25*(-1-2) + 0.25*(-1-2) + 0.25*(-1-2) + 0.25*(-1-1.7)
- Policy Improvement
- 基于当前的状态价值函数(value function),用贪心算法找到最优策略
π ′ ( s ) = arg max a ∈ A q π ( s , a ) \pi'(s)=\arg\max_{a\in A} q_{\pi}(s,a) π′(s)=arga∈Amaxqπ(s,a)
- v π v_\pi vπ会一直迭代到收敛,具体证明如图:
- 扩展
- 事实上在大多数情况下 Policy evaluation 不必要非常逼近最优值,这时我们通常引入 $ \epsilon-convergence $ 函数来控制迭代停止
- 很多情况下价值函数还未完全收敛,Policy 就已经最优,所以在每次迭代之后都可以更新策略(Policy),当策略无变化时停止迭代
2.Value Iteration
- 最优化原理:当且仅当状态 s s s 达到任意能到达的状态 s ′ s' s′ 时,价值函数 v v v 能在当前策略(policy)下达到最优,即 v π ( s ′ ) = v ∗ ( s ′ ) v_{\pi}(s') = v_*(s') vπ(s′)=v∗(s′),与此同时,状态 s 也能基于当前策略达到最优,即 v π ( s ) = v ∗ ( s ) v_{\pi}(s) = v_*(s) vπ(s)=v∗(s)
- 状态转移公式为: v k + 1 ( s ) = max a ∈ A ( R s a + γ ∑ s ′ ∈ S P s s ′ a v k ( s ′ ) ) v_{k+1}(s) = \max_{a\in A}(R^a_s+\gamma\sum_{s' \in S}P^a_{ss'}v_k(s')) vk+1(s)=maxa∈A(Rsa+γ∑s′∈SPss′avk(s′))
- 矩阵形式为: v k + 1 = max a ∈ A R s a + γ P a v k \mathbf{v_{k+1}} =\max_{a \in A} \mathbf{R^a_s} +\gamma\mathbf{P^av_k} vk+1=maxa∈ARsa+γPavk
- 下面是一个实例,求每个格子到终点的最短距离,走一步的 reward 是 -1:

同步动态规划算法小结
1.迭代策略评估(Iterative Policy Evaluation)解决的是 Prediction 问题,使用了贝尔曼期望方程(Bellman Expectation Equation)
2.策略迭代(Policy Iteration)解决的是 Control 问题,实质是在迭代策略评估之后加一个选择 Policy 的过程,使用的是贝尔曼期望方程和贪心算法
3.价值迭代(Value Iteration) 解决的是 Control 问题,它并没有直接计算策略(Policy),而是在得到最优的基于策略的价值函数之后推导出最优的 Policy,使用的是贝尔曼最优化方程(Bellman Optimality Equation)
Model-free v.s. Model-based
Model-based 是指学习 Transition Model T ( S , a , S ′ ) ∼ P r ( s ′ ∣ s , a ) T(S, a, S') \sim P_r(s'|s, a) T(S,a,S′)∼Pr(s′∣s,a) ,即在状态 s 采取行动 a 后转移到 s’ 的概率,然后基于这个 Model 去选择最优的策略。Transition Model 的空间复杂度为 O ( S 2 A ) O(S^2 A) O(S2A) ,所以不太适合用于解决状态空间和动作空间过大的问题。
Model-free 未知 Transition Model,通常通过不断的尝试去直接学习最优策略。
前面的 Policy Iteration 和 Value Iteration 都是 model-based 方法,因此一定程度上受限于状态空间和动作空间的规模。于是 Q-learning 应运而生。
Q-learning
公式如下,可以看出 Q-leaning 由 Value iteration 演变而来,但去除了对 Transition Model 的依赖,因此属于 Model-free 的方法。另一方面下一个动作 a 的选择,原来是根据 policy 选择最优的 action,现在是 maximum 下一个 state 的值来选择 action,所以 Q-learning 属于 off-policy (离线) 算法。
Q ( s t , a t ) ← ( 1 − α ) Q ( s t , a t ) + α [ r t + 1 + γ max a Q ( s t + 1 , a ) ] Q(s_t, a_t)\leftarrow (1-\alpha)Q(s_t, a_t) + \alpha[r_{t+1} + \gamma \max_{a} Q(s_{t+1}, a)] Q(st,at)←(1−α)Q(st,at)+α[rt+1+γamaxQ(st+1,a)]
State-Action-Reward-State-Action (SARSA)
公式如下,唯一与 Q-learning 的不同是,SARSA 是 on-policy 方法,需要考虑 exporation-exploitation 问题,基本方法是 ϵ − g r e e d y \epsilon-greedy ϵ−greedy 。
Q ( s t , a t ) ← ( 1 − α ) Q ( s t , a t ) + α [ r t + 1 + γ Q ( s t + 1 , a t + 1 ) ] Q(s_t, a_t) \leftarrow (1-\alpha)Q(s_t,a_t) + \alpha[r_{t+1} + \gamma Q(s_{t+1}, a_{t+1})] Q(st,at)←(1−α)Q(st,at)+α[rt+1+γQ(st+1,at+1)]
S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)是单步更新和回合更新的结合。
当 lambda 取0,就变成了 Sarsa 的单步更新,当 lambda 取 1,就变成了回合更新,对所有步更新的力度都是一样。当 lambda 在 0 和 1 之间,取值越大,离宝藏越近的步更新力度越大。这样我们就不用受限于单步更新的每次只能更新最近的一步,我们可以更有效率的更新所有相关步了。
Deep Q Network(DQN)
基本思路是,用神经网络建模 Q function,基本公式如下:
y j = r j + γ max a ′ Q ( ϕ j + 1 , a ′ , θ − ) y_j = r_j + \gamma \max_{a'}Q(\phi_{j+1},a',\theta^-) yj=rj+γa′maxQ(ϕj+1,a′,θ−)
其中, ϕ \phi ϕ是state s, θ \theta θ代表网络参数。Loss为网络输出值 Q ( ϕ j + 1 , a ′ , θ ) Q(\phi_{j+1},a',\theta) Q(ϕj+1,a′,θ) 和目标值 y i y_i yi 之间的平方误差。
- Experience Replay
- Fix Q-targets
同时,因为训练样本并不满足 iid,DQN 引入 Experience Replay 机制从 replay 中随机采样数据以尽量减少样本间的相关性,使得网络更容易训练。另外,DQN 的 target network 和 estimate network 结构一致,经过 C 轮迭代之后更新 target network = estimate network,从而使训练更稳定。
pytorch实现DQN
这里基于gym库里的‘CartPole-v0’游戏,通过Pytorch搭建DQN网络进行强化学习的训练,测试训练效果。
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import gym
# Hyper Parameters
BATCH_SIZE = 32
LR = 0.01 # learning rate
EPSILON = 0.9 # greedy policy
GAMMA = 0.9 # reward discount
TARGET_REPLACE_ITER = 100 # target update frequency
MEMORY_CAPACITY = 2000
env = gym.make('CartPole-v0') # 立杆子游戏
env = env.unwrapped
N_ACTIONS = env.action_space.n
print("action_space:", N_ACTIONS)
N_STATES = env.observation_space.shape[0]
print("state_space:", N_STATES)
ENV_A_SHAPE = 0 if isinstance(env.action_space.sample(), int) else env.action_space.sample().shape # to confirm the shape
class Net(nn.Module):
def __init__(self, ):
super(Net, self).__init__()
self.fc1 = nn.Linear(N_STATES, 50)
self.fc1.weight.data.normal_(0, 0.1) # initialization
self.out = nn.Linear(50, N_ACTIONS)
self.out.weight.data.normal_(0, 0.1) # initialization
def forward(self, x):
x = self.fc1(x)
x = F.relu(x)
actions_value = self.out(x)
return actions_value
class DQN(object):
def __init__(self):
self.eval_net, self.target_net = Net(), Net()
self.learn_step_counter = 0 # for target updating
self.memory_counter = 0 # for storing memory
self.memory = np.zeros((MEMORY_CAPACITY, N_STATES * 2 + 2)) # initialize memory
self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=LR)
self.loss_func = nn.MSELoss()
def choose_action(self, x):
x = torch.unsqueeze(torch.FloatTensor(x), 0)
# input only one sample
if np.random.uniform() < EPSILON: # greedy
actions_value = self.eval_net.forward(x)
action = torch.max(actions_value, 1)[1].data.numpy()
action = action[0] if ENV_A_SHAPE == 0 else action.reshape(ENV_A_SHAPE) # return the argmax index
else: # random
action = np.random.randint(0, N_ACTIONS)
action = action if ENV_A_SHAPE == 0 else action.reshape(ENV_A_SHAPE)
return action
def store_transition(self, s, a, r, s_):
transition = np.hstack((s, [a, r], s_))
# replace the old memory with new memory
index = self.memory_counter % MEMORY_CAPACITY
self.memory[index, :] = transition
self.memory_counter += 1
def learn(self):
# target parameter update
if self.learn_step_counter % TARGET_REPLACE_ITER == 0:
self.target_net.load_state_dict(self.eval_net.state_dict())
self.learn_step_counter += 1
# sample batch transitions
sample_index = np.random.choice(MEMORY_CAPACITY, BATCH_SIZE)
b_memory = self.memory[sample_index, :]
b_s = torch.FloatTensor(b_memory[:, :N_STATES])
b_a = torch.LongTensor(b_memory[:, N_STATES:N_STATES+1].astype(int))
b_r = torch.FloatTensor(b_memory[:, N_STATES+1:N_STATES+2])
b_s_ = torch.FloatTensor(b_memory[:, -N_STATES:])
# q_eval w.r.t the action in experience
q_eval = self.eval_net(b_s).gather(1, b_a) # shape (batch, 1)
q_next = self.target_net(b_s_).detach() # detach from graph, don't backpropagate
q_target = b_r + GAMMA * q_next.max(1)[0].view(BATCH_SIZE, 1) # shape (batch, 1)
loss = self.loss_func(q_eval, q_target)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
dqn = DQN()
print('\nCollecting experience...')
for i_episode in range(400):
s = env.reset()
ep_r = 0
while True:
env.render()
a = dqn.choose_action(s)
# take action
s_, r, done, info = env.step(a)
# modify the reward
x, x_dot, theta, theta_dot = s_
r1 = (env.x_threshold - abs(x)) / env.x_threshold - 0.8
r2 = (env.theta_threshold_radians - abs(theta)) / env.theta_threshold_radians - 0.5
r = r1 + r2
dqn.store_transition(s, a, r, s_)
ep_r += r
if dqn.memory_counter > MEMORY_CAPACITY:
dqn.learn()
if done:
print('Ep: ', i_episode,
'| Ep_r: ', round(ep_r, 2))
if done:
break
s = s_
Deep Deterministic Policy Gradient (DDPG)
DQN 可以很好的解决高维状态空间问题,但对连续动作空间或者是动作空间非常大的情况并不适用。DDPG 尝试通过 actor-critic architecture 来解决连续动作空间的问题,引入 actor 输出连续动作(离散也可以),critic 则是对状态,动作对(s,a)打分,指导 actor 的学习。
DDPG 也采用了 DQN 的 Seperate Target Network 机制,critic 和 actor 各有两个神经网络,一类是 target,一类用于 estimate(即会即时更新的 network)。
- Actor
- Actor Network (estimation) μ ( s i ∣ θ μ ) \mu(s_i|\theta^\mu) μ(si∣θμ)
- Target Network μ ′ ( s i + 1 ∣ θ μ ) \mu'(s_{i+1}|\theta^{\mu}) μ′(si+1∣θμ)
- Critic
- Critic Network (estimation) Q ( s i , a i ∣ θ Q ) Q(s_i,a_i|\theta^Q) Q(si,ai∣θQ)
- Target Network Q ( s i + 1 , μ ′ ( s i + 1 ∣ θ μ ′ ) ∣ θ Q ′ ) Q(s_{i+1}, \mu'(s_{i+1}|\theta^{\mu'})|\theta^{Q'}) Q(si+1,μ′(si+1∣θμ′)∣θQ′)
其中还有几个值得注意的点:
- 不同于 DQN 每过 C 次迭代将 estimation network 的参数直接复制到 target network,DDPG 使用 soft target update( θ ′ ← τ θ + ( 1 − τ ) θ ′ w i t h τ ≪ 1. \theta' \leftarrow \tau\theta + (1-\tau)\theta' \;with\; \tau \ll 1. θ′←τθ+(1−τ)θ′withτ≪1.) 保证参数缓慢更新
- 引入了 batch normalization
- 通过给参数空间或动作空间加入 noise 鼓励 actor 进行 exploration (Open AI 发现把 noise 加入在参数上效果更好,见 blog post)
PG 和 Q learning 的问题
Policy Gradient 的问题是,1)大的策略更新使训练失败,2)有时很难将策略的变化映射到参数空间,3)不合适的学习率导致梯度消失或爆炸,4)样本效率(sample efficiency)低。
Q learning 的问题 是,大部分情况下,对不同的 action 差别不会很大(方差小),且在部分任务中,Q function 的值总为正。
优势函数 Advantage Function
优势函数就是为了解决 Q function 值方差小而引入的,基本形式为 A ( s , a ) = Q ( s , a ) − V ( s ) = E s ′ ∼ P ( s ′ ∣ s , a ) [ r ( s ) + γ V π ( s ′ ) − V π ( s ) ] A(s,a) = Q(s,a) - V(s)=E_{s'\sim P(s'|s,a)}[r(s) + \gamma V^\pi(s')-V^\pi(s)] A(s,a)=Q(s,a)−V(s)=Es′∼P(s′∣s,a)[r(s)+γVπ(s′)−Vπ(s)]
A ( s , a ) A(s,a) A(s,a) 意义为当前 (s,a) pair 的效用相对于该状态下平均效用的大小,如果大于 0 则说明该动作优于平均动作。
其中 Q π ( s t , a t ) Q_π(s_t,a_t) Qπ(st,at)可以使用从当前状态开始到eposide结束的奖励折现和得到, V π ( s t ) V_π(s_t) Vπ(st)可以通过一个critic来计算得到。
Trust Region Policy Optimization (TRPO)
实作 DDPG 的一个问题网络参数更新的步长不好确定,太小网络优化会非常慢,太大则容易优化过头,导致更新后的网络反而不如更新之前。为此 TRPO 想通过一个机制使回报函数在更新的过程中单调递增,即 expected discounted long-term reward η \eta η 递增。
η ( π ) = E s 0 , a 0 , . . . [ ∑ t = 0 ∞ γ t r ( s t ) ] \eta(\pi)=E_{s_0,a_0,...}\left[\sum_{t=0}^\infty \gamma^t r(s_t) \right] η(π)=Es0,a0,...[t=0∑∞γtr(st)]
为使每次迭代后 η \eta η 保持增加,直观的想法是将其分解为旧策略对应的回报函数+其他项,然后设法保证其他项大于等于零即可。该分解公式如下:(具体推导可参见:https://arxiv.org/pdf/1509.02971.pdf)。1
η ( π ~ ) = η ( π ) + E s 0 , a 0 , . . . , ∼ π ~ [ ∑ t = 0 ∞ γ t A π ( s t , a t ) ] \eta(\tilde{\pi}) = \eta(\pi) + E_{s_0,a_0,...,\sim \tilde{\pi}}\left[\sum_{t=0}^\infty \gamma^t A_\pi(s_t,a_t) \right] η(π~)=η(π)+Es0,a0,...,∼π~[t=0∑∞γtAπ(st,at)]
第一项旧策略回报值,第二项为新旧策略的回报差值。上式又可以进一步转化为
η ( π ^ ) = η ( π ) + ∑ s ρ π ^ ( s ) ∑ a π ^ ( a ∣ s ) A π ( s , a ) ρ π ( s ) = P ( s 0 = s ) + γ P ( s 1 = s ) + γ 2 P ( s 2 = s ) + . . . \eta(\hat{\pi}) = \eta(\pi)+\sum_s \rho_{\hat{\pi}}(s)\sum_a \hat{\pi}(a|s)A^\pi(s,a) \\ \rho_{\pi}(s)=P(s_0=s)+\gamma P(s_1=s)+\gamma^2P(s_2=s)+... η(π^)=η(π)+s∑ρπ^(s)a∑π^(a∣s)Aπ(s,a)ρπ(s)=P(s0=s)+γP(s1=s)+γ2P(s2=s)+...
但 η ( π ^ ) \eta(\hat{\pi}) η(π^) 非常依赖新策略导致很难优化,所以我们忽略状态分布的变化,保持旧策略对应的状态分布,引入对 η ( π ^ ) \eta(\hat{\pi}) η(π^) 的近似 L π ( π ^ ) L_\pi(\hat\pi) Lπ(π^) 作为优化目标:
L π ( π ^ ) = η ( π ) + ∑ s ρ π ( s ) ∑ a π ^ ( a ∣ s ) A π ( s , a ) L_\pi(\hat\pi)=\eta(\pi)+\sum_s \rho_\pi(s)\sum_a \hat\pi(a|s)A_\pi(s,a) Lπ(π^)=η(π)+s∑ρπ(s)a∑π^(a∣s)Aπ(s,a)
式中的动作 a 还是依赖于新策略,而新策略由未知的参数 [公式] 决定,所以我们引入重要性采样(importance sampling)对动作分布进行处理。
∑ a π ^ ( a ∣ s ) A π ( s , a ) = E a , q [ π ^ θ ( a ∣ s n ) q ( a ∣ s n ) A θ o l d ( s n , a ) ] \sum_a \hat\pi(a|s)A_\pi(s,a)=E_{a,q}\left[ \frac{\hat\pi_\theta(a|s_n)}{q(a|s_n)} A_{\theta_{old}}(s_n,a) \right] a∑π^(a∣s)Aπ(s,a)=Ea,q[q(a∣sn)π^θ(a∣sn)Aθold(sn,a)]
最后再通过一些变换,以及引入平均 KL-divergence 可将问题转化为:(过程可参考原论文或https://zhuanlan.zhihu.com/p/26308073)
引入 KL-divergence 的目的是限制新旧策略的的差别,防止更新太过发散。
Proximal Policy Optimization (PPO)
η For New Policy π’ (https://arxiv.org/pdf/1509.02971.pdf) ↩︎