一维线搜索确定最优步长

目录

1. 一维搜索问题
2. 进退法确定搜索区间
3. 分割技术（0.618）减小搜索区间
4. wolfe条件确定步长
   4.1 梯度与函数下降的关系？
   4.2 wolfe条件

1.一维搜索问题

一维线搜索，就是指单变量函数的最优化，它是专门针对单峰函数设计的：

如上一篇文章所述，多变量函数中，迭代格式为：

xk+1=xk+αkdk

其中的关键就在于找到合适的步长 αk,和搜索方向dk. 可以设：

ϕ(α)=f(xk+αdk)

从初始点 xk 出发，以步长 αk 沿着搜索方向搜索，使得：

ϕ(αk)<ϕ(0)

的问题，就是所谓的关于 α 的一维搜索问题。
如果能找到 αk 使得：

f(xk+αkdk)=minα>0f(xk+αdk)

其中 αk 就是最优的步长因子。

关键还是怎么得到这样的 αk ,在一维搜索中，其主要的想法就是先确定一个搜索区间，然后采用插值法或者分割技术逐渐减小这个区间，直到找到最优的 αk .

2.进退法确定搜索区间

搜索区间，相当于满足 α∗>0的同时， 使得：

ϕ(α∗)=minα>0ϕ(α)

的 α∗ 所在的区间[a,b]（ α∗∈[a,b] ），且该区间必定会大于0，称该区间称为搜索区间。

其中确定搜索区间的方法之一就是进退法：

• 从一点出发，试图确定函数值的高-低-高三点，沿着搜索方向搜索，如果一个方向不成功，就退回来，沿着相反方向搜索。这样只需比较一个点的函数值大小，就可以确定了。

算法步骤如下：

1. α0∈[0,+∞),h0>0,k:=0,计算ϕ(α0)
2. 比较目标函数值，令 αk+1=αk+hk ,计算 ϕ(αk+1),若ϕ(αk+1)<ϕ(αk) ,转到第三步
3. 加大搜索步长 hk−1:=t∗hk(t一般取2),α:=αk,αk:=αk+1,ϕ(αk):=ϕ(αk+1) 转至第二步
4. 反向搜索；若k=0,令 hk:=−hk,αk:=αk+1,转至第二步。否则停止迭代， 得到
   a=min(α,αk+1),b=max(α,αk+1)
   输出，a,b
   过程如图所示：

3.分割技术（0.618）减小搜索区间

前面介绍了怎么用进退法确定我们的搜索区间，但区间那么大，也不好求出最优化，因此可以通过切割区间，来减小区间，0.618和Fibonacci就是这样的分割方法。

• 它们的基本思想都是通过取试探点，进行函数值比较，使包含极小点的搜索区间逐渐减小，当区间长度缩小到一定程度时，可以认为区间内的点均为极小点的近似。

0.618法是针对以上的单峰函数的，可以设

ϕ(α)=f(xk+αdk)

是搜索区间 [a0,b0] 上的单峰函数

第一步迭代：
1. 要求 λk,μk 到搜索区间的两个端点等距;
2. 每次迭代，要求搜索区间的缩短率相同；

用数学表达式表达出来如下：

第二次迭代：

由此得到

迭代到一定条件之后，可以求出我们最初要求的参数：

αk=(λk+μk)2

此外，还有一些分割方法，比如Fibonacci，它和0.618法的主要区别是它的缩短率不是采用黄金分割数，而是采用了Fibonacci数，Fibonacci数列满足：

F0=F1=1,Fk+1=Fk+Fk−1

,详细的推导请参考袁亚湘老师的 最优化理论与方法p73.

4.wolfe条件确定步长

在一些实际问题中，目标函数如果不可微，就可以采用0.618法来确定步长，但也有很多情况下目标函数是可微的，一旦可微，我们就可以计算他们的梯度了。

4.1 梯度与函数下降的关系？

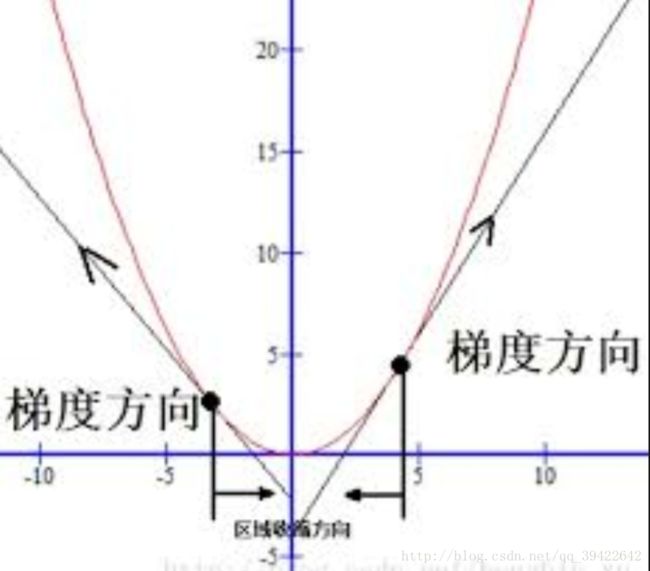
很多人有这样的疑问，梯度有什么用？
如图所示为梯度方向，如果梯度小于0，则必然是相反方向，也就是函数下降的方向，这是一个直观的看法，下面用公式证明这个结论。

定义：设 f 是 Rn上的实函数，d∈Rn。 若存在某个正数 α⎯⎯>0使得

f(x+αd)<f(x),∀α∈(0,α⎯⎯)

则称d是f在x处的一个下降方向，相关系数 α 称为一个步长。（这个是下降方向的数学表达式，满足这个条件的就是下降方向）

再给出一个定理：设 f:是Rn→R 在x处可微，若存在 d∈Rn 使得

∇f(x)Td<0,

则d必为 f(x) 在x处的一个下降方向。

为了看一下这个的准确性，现在给出证明。

证明：由Taylor定理，对于任意的 α>0, 我们有

f(x+αd)=f(x)+α∇f(x)Td+o(||αd||)

既然 ∇f(x)Td<0,从而必然存在α⎯⎯>0, 使得当 α∈(0,α⎯⎯) 时，

∇f(x)Td+o(||αd||)α<0

于是

f(x+αd)=f(x)+α∇f(x)Td+o(||αd||)<f(x)

得证。

由此我们发现，只要 ∇f(x)≠0, 那么下降方向 d 一定存在，因为即使 ∇f(x)>0, 我们可以取它的负方向作为下降方向。

4.2 wolfe条件

大于0的正数 α 作为步长，在函数下降方向总有：

Armijo条件：f(x+αd)=f(x)+cα∇f(x)Td,   0<c<1

但直接用该条件确定步长有可能使得步长太小，故使用后退技巧：选取 0<t<1 ,找到一个最小的非负整数j，使得

f(x+tjd)≤f(x)+ctj∇f(x)Td,

令步长为 α=tj .

如果该条件加上曲率条件，就构成了Wolfe条件：

Armijo条件：f(x+αd)=f(x)+c1α∇f(x)Td,

曲率条件：∇f(x+αd)Td≥c2∇f(x)Td,

其中 0<c1<c2<1.

参考

最优化理论与方法 –袁亚湘
最优化选讲