深入理解计算机系统（原书第三版）笔记（二） 2.2整数表示

知识点：

整数在计算机上的储存形式及编码

思考

整形在C语言的表示中，同一数据类型，能表示的最小负数和最大正数的绝对值是不同的。 比如[signed]char最小值为-128，最大值是127，这是什么造成的呢？

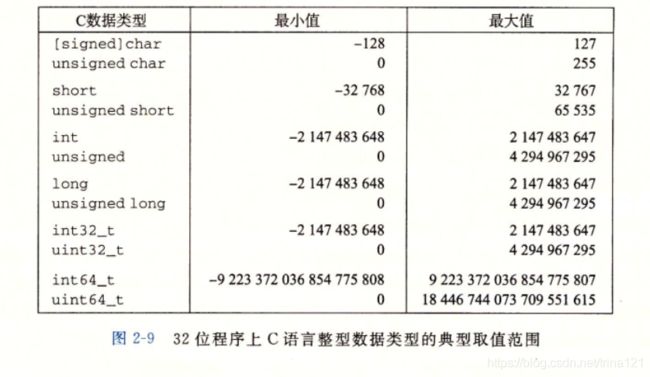
前面的文章我们提到，在计算机中，
信息就是位+上下文

即:

系统中的所有信息-----包括磁盘文件，内存中的程序，内存中存放的用户数据，及网上传送的数据，都是由一串比特表示的。(形如10010这样的二进制数据)

区分这些数据对象的唯一方法是我们读到这些数据对象时的上下文。比如在不同的上下文中，一个同样的字节序列可能表示一个整数,浮点数,字符串或者机器指令。(比特(bit)即“位”,是计算机中信息量的最小单位, 8 比特(bit) = 1字节 (byte)).

eg: “1”在不同的上下文中既可以表示数量1，也可以作为布尔变量来表示true。

那么为了沟通方便，我们就有了约定俗成的编码来规定在某些上下文中对位的解释，从而传递信息。

整数的编码

无符号数编码

此编码的规则，我们可以用一个函数来表示:B2U_w(Binary to Unsigned，长度为w)
$$B2U_w(x)=\sum _{i=0}^{w-1}{x}_i{2}^i$$
那么通过把一串比特看作是以无符号数编码方式编码的信息的话
我们可以得到
eg:

$$B2U_4([0001])=0\ast 2^3+0\ast 2^2+0\ast 2^1+1\ast 2^0=1$$
$$B2U_5（[10101]）=1\ast 2^4+0\ast 2^3+1\ast 2^2+0\ast 2^1+1\ast 2^0=21$$

有符号数编码

补码编码 （two’s-complement）

此编码的规则，我们可以用一个函数来表示:B2T_w(Binary to Unsigned，长度为w)
$$B2T_w(x)=x_{w-1}{2}^{w-1}+\sum _{i=0}^{w-2}{x}_i{2}^i$$
即最高位x_w-1的权重为-2^w-1,其他位x_k的权重为2^k。
eg:
$$B2T_4（[0001]）=0\ast -2^3+0\ast 2^2+0\ast 2^1+0\ast 2^0=1$$
$$B2T_5（[10101]）=0\ast -2^4+0\ast 2^3+0\ast 2^2+0\ast 2^1{+}^0\ast 2^0=-11$$

由此可以表示负的整数，通常我们在计算机中的有符号数表示方式是补码形式。

那么我们可以回答最开始的问题。

整形在C语言的表示中，同一数据类型，能表示的最小负数和最大正数的值是不同的。
比如[signed]char最小值为-128，最大值是127，这是什么造成的呢？

以8位比特串为例，能表达的

最大值为
$$B2T9([01111111])=127$$
最小值为
$$B2T9([10000000])=-128$$
此外还有两种其他的有符号数表示方法:反码(Ones’ Complement),原码(Sign-Magnitude)

反码编码(Ones’ Complement)

除了最高有效位的权重是-(2^w-1-1)而不是-2^w-1，它和补码是一样的
$$B2O_w(x)=x_{w-1}(2^{w-1}-1)+\sum _{i=0}^{w-2}{x}_i{2}^i$$

原码编码(Sign-Magnitude)

最高有效位是符号位，来决定剩下的位取正权还是负权
$$B2S_w(x)=(-1{)}^{x_{w-1}}\ast (\sum _{i=0}^{w-2}{x}_i{2}^i)$$

反码和原码的特点

反码和原码这两种编码方式都有个奇怪的特点:对数字0有两种表示方式
反码中：[00000]=+0,[11111] = -0
原码中：[00000]=+0,[10000] = -0

而无符号数编码和补码具有唯一性
即B2T_U和B2T_w函数是双射:每个函数值都与变量值一对一相对应。

虽然有的过去有的机器基于反码，但几乎所有现代机器使用补码，我们将在浮点数中看到原码编码。

数据的转换

有符号数和无符号数的转换

在C语言中，有符号数和无符数转换规则:数值可能会变，但位模式保持不变。
只改变对于一串比特的解释方式，不改变底层的值。
eg:在如下程序中

short int v =-12345;
unsigned short uv =(unsigned short) v;
printf("v= %d, us = %u\n",v,uv);

在使用补码机器上输出为

v=-12345 , uv=53191

short为16位
$$v=1100111111000111$$
$$uv=1100111111000111$$
但解释方式不同
$$B2U_{16}(v)=-12345$$
$$B2T_{16}(uv)=53191$$

扩展一个数的位

• 如果两个数的位数不同，比如8bit的数如何和16bit的数运算呢？

我们需要扩展一个数的位，使8bit成为16bit
扩展位时，数的值不改变

无符号数的零扩展(zero extension)

在最大端加入0
eg:x(8 bit)=10000001->x(16 bit)=0000000010000001

补码数的符号扩展(sign extension)

在最大端加入与最高有效位相同的值
eg:x(8 bit)=00000001->x(16 bit)=0000000010000001
x(8 bit)=10000001->x(16 bit)=1111111110000001

在如下程序中:

short sx=-12345; /*-12345*/
unsigned shor ussx =sx; /*53191*/
int x= sx;  /*-12345*/
unsigned ux = usx;  /*53191*/

得出结果

sx = -12345; cf c7 <-（16进制数表示）
usx = 53191; cf c7
x = -12345; ff ff cf c7
ux = 53191; 00 00 cf c7

只有无符号有符号之间转换时，数的值才发生改变

截断数字

eg:当我们进行32bit类型到16bit类型的转换时候，我们直接截断高位的16位数字

int x= 53191;     /*x:00000000000000001100111111000111*/
short sx = (short) x;  /*sx:1100111111000111   值为-12345  (截断)*/
int y = sx;  /*y:11111111111111111100111111000111   值为-12345 (扩展)*/

根据C语言的标准，我们要先改变大小再进行符号转换

即(unsigned) sx 等价于(unsigned)( int) sx 但是不等价于(unsigned)(unsigned short) sx。

整数之间是如何运算的 见我的另一篇博客

练习题

练习题2.25

题目 ：

考虑如下代码，这段代码试图计算数组a中所有元素的和，其中元素的数量由参数length给出。

当参数 length等于0时，运行这段代码应该返回0.0。但实际上，运行时会遇到一个内存错误。请解释为什么会发生这样的情况，并且说明如何修改代码。

/* WARNING : This i buggy code */
float sum_elements(float a[],unsigned length){
     
int i;
float result=0;

for(i=0;i<=length-1;i++){
     
result+=a[i];
return result;

}

}

答:

发生错误的语句在于i<=length-1该语句等于i<=length+(-1)。我们知道负数在计算机中一般使用补码表示，以位来看，-1的二进制形式为1111111…

此处涉及到*C语言的隐式转换。length是 unsigned 格式，那么 -1的二进制码将被视为unsigned格式，即最高位所代表的权重由负值转为极大正值所以i<=length-1恒成立。会造成地址溢出，并且位于kernal地址的数据外泄。

*C语言中两数计算时，短数据数格式会自动转换为长数据数的格式

修改:

1.把函数的输入的length声明格式由unsigned改为Int

          或

2.将for循环的条件改为i

参考及来源:

Randal E. Bryant., David R. O’Hallaron, Gong, Y., & He, L. (2016). Shen ru li jie ji suan ji xi tong =. Beijing: Ji xie gong ye chu ban
she.