ACM Plan - UVa 10779 Collector’s Problem(网络流模板题)

题意

Bob 和朋友换贴纸，他和朋友们都有若干贴纸，Bob 希望通过交换来使自己持有更多种类的贴纸，给出每个人的贴纸持有信息，求Bob 经过交换后能持有的最大贴纸种类数。

Input

格式：
先给出样例数量，每个样例第一行给出参与交换的人数n（包括Bob）和参与交换的贴纸种类数m，接着n行，每行描述一个人，第一行为Bob。先给出此人拥有的贴纸数k，而后k个数代表贴纸的种类

2
2 5
6 1 1 1 1 1 1
3 1 2 2
3 5
4 1 2 1 1
3 2 2 2
5 1 3 4 4 3

Output

Case #1: 1
Case #2: 3

思路

很标准的网络流模板题，只要求一个数，不要求打印方案，稍微有点绕，就是起点和终点都是Bob，可以分成两个Bob。

网络流最重要是建好图（以下边均为单向边），
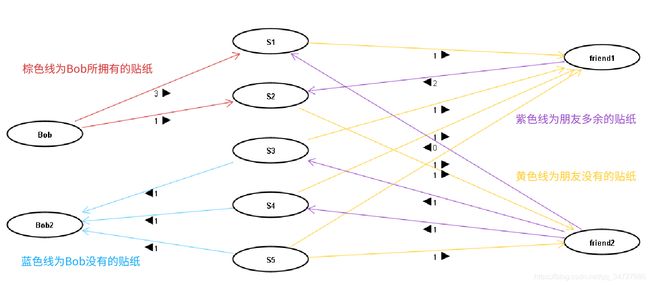
首先连接 Bob—>他拥有的贴纸建边，权重为Bob持有的该种类贴纸数；
对贴纸和朋友建边，连接 朋友所没有的贴纸—>朋友，权重为1，表示该朋友缺少1张该种类的贴纸；
而后连接 朋友—>朋友多余的贴纸，权重为所持有贴纸数量-1，表示该朋友可以拿出来交换的贴纸；
最后连接 Bob没有的贴纸—>Bob，权重为1，表示Bob 缺少1张该种类的贴纸；

建好图后，直接一个dinic或者edmonds_karp求出答案即可。

样例一图示（这里为了看的清楚没有标出残余图的边）：

样例二图示（剩余图的边没有标出）：

Code

代码前面为网络流两个算法的模板

#include 
#define inf 0xfffffff
using namespace std;
typedef vector<int> vi;
typedef pair<int, int> II;
struct EDGE{
     
    int u, v, cap, flow;
    EDGE(){
     }
    EDGE(int a, int b, int c, int d):
        u(a), v(b), cap(c), flow(d){
     }
};

vector<EDGE> EL;
vector<vi> AL;
vi d, last;
vector<II> p;
int cnt;

bool BFS(int s, int t){
     
    d.assign(cnt, -1); d[s] = 0;
    queue<int> q; q.push(s);
    p.assign(cnt, {
     -1, -1});
    while(!q.empty() && d[t] == -1){
     
        int u = q.front(); q.pop();
        for(int i = 0; i < AL[u].size(); ++i){
     
            auto& e1 = EL[AL[u][i]];
            if(e1.cap > e1.flow && d[e1.v] == -1)
                d[e1.v] = d[e1.u] + 1, q.push(e1.v), p[e1.v] = {
     e1.u, AL[u][i]};
        }
    }
    return d[t] != -1;
}

int DFS(int s, int t, int f){
     
    if(s == t || f == 0) return f;
    for(; last[s] < AL[s].size(); ++last[s]){
     
        auto& e1 = EL[AL[s][last[s]]];
        if(d[e1.v] != d[e1.u] + 1) continue;
        int pushed = DFS(e1.v, t, min(f, e1.cap - e1.flow));
        if(pushed > 0){
     
            e1.flow += pushed;
            auto& e2 = EL[AL[s][last[s]]^1];
            e2.flow -= pushed;
            return pushed;
        }
    }
    return 0;
}

int send_one_flow(int s, int t, int f){
     
    if(s == t) return f;
    auto& pa = p[t];
    auto& e1 = EL[pa.second];
    int pushed = send_one_flow(s, pa.first, min(f, e1.cap - e1.flow));
    e1.flow += pushed;
    auto& e2 = EL[pa.second^1];
    e2.flow -= pushed;
    return pushed;
}

int edmonds_karp(int s, int t){
     
    int mf = 0;
    while(BFS(s, t)){
     
        int f = send_one_flow(s, t, inf);
        if(f == 0) break;
        mf += f;
    }
    return mf;
}

int dinic(int s, int t){
     
    int mf = 0;
    while(BFS(s, t)){
     
        last.assign(cnt, 0);
        while(int f = DFS(s, t, inf))
            mf += f;
    }
    return mf;
}

void init(){
     
    EL.clear();
    AL.assign(cnt, vi());
}

void add_edge(int u, int v, int w, int directed){
     
    if(u == v) return ;
    EL.emplace_back(u, v, w, 0);
    AL[u].push_back(EL.size() - 1);
    EL.emplace_back(v, u, directed ? 0 : w, 0);
    AL[v].push_back(EL.size() - 1);
}

int num[12][28];

int main(){
     
    int t, c = 1; cin >> t;
    while(t--){
     
        int n, m; cin >> n >> m;
        cnt = n + m + 2;
        memset(num, 0, sizeof(num));
        for(int i = 0; i < n; ++i){
     
            int sum; cin >> sum;
            for(int j = 0; j < sum; ++j){
     
                int v; cin >> v;
                ++num[i][v];//统计所有人的贴纸拥有数
            }
        }

        init();
        for(int i = 1; i <= m; ++i)
            add_edge(0, i, num[0][i], 1);/建立Bob到贴纸的单向边
        for(int i = 1; i < n; ++i){
     
            for(int j = 1; j <= m; ++j){
     
                if(num[i][j] == 0) add_edge(j, i + m, 1, 1);//建立贴纸到朋友的单向边
                else add_edge(m + i, j, num[i][j] - 1, 1);//建立朋友到贴纸的单向边
            }
        }
        for(int i = 1; i <= m; ++i){
     
            add_edge(i, cnt - 1, 1, 0);//建立贴纸到Bob2的单向边
        }
        cout << "Case #" << c++ << ": " << dinic(0, cnt - 1) << endl;
    }
}