地图兴趣点聚合算法的探索与实践
一、导读
在实现基于地图的业务时,当地图上需要展示的兴趣点(POI)过多时,一般会基于图面效果和渲染性能的考虑,在大比例尺展示完整的业务数据,而在小比例尺展示聚合态数据。在处理不同数量级、不同分布形态的POI时,如何通过算法取得更加合理的聚合效果,同时既能支持离线的预处理聚合,也能较好的满足实时聚合的性能要求是本文主要讨论的内容。
注:兴趣点(Point of Interest,通常缩写成POI)是指电子地图上的某个地标、景点,用以标示出该地所代表的政府机关、商业机构(加油站、超市、餐厅、酒店等)、风景名胜、公共厕所、交通设施等处所。
本文通过对现有聚合算法进行预研,并结合实际业务对其进行改进,构建了一套能够满足多种业务需求的数据聚合方案。其中包含多种针对不同业务场景、不同数量级的POI聚合算法,并将聚合算法的配置进行了抽象,实现了聚合效果好,性能高且使用方便的聚合算法库,目前已应用到离线聚合和线上实时聚合的各个业务场景中。
二、点聚合算法比较
本节介绍目前使用较多的点聚合算法,并对不同点聚合算法的性能和聚合效果进行横向对比。针对不同的场景给出了参考使用的点聚合算法。在此基础上构建了一套相对通用的点聚合算法工具,使用者可以根据自身业务的特点,通过一定的配置来自定义具体使用的算法、策略和参数等等。
2.1 点聚合算法:
这里对使用较多的点聚合方案做简单介绍。
2.1.1 kmeans算法
kmeans算法主要通过初始指定k个聚类质心,而后按照“距离”来聚拢“相近”的数据点,而后重新计算新的质心,以此往复。不断迭代计算k个聚类点的质心,最终回归到k个聚类结果中,主要有以下两个缺点:
性能, kmeans是计算密集型算法,模型需要迭代很多次才能够完善,且大量的距离计算比较消耗cpu。
效果,kmeans不能解决重叠覆盖问题(算法设计指标里边没有对覆盖问题的评估指标)。
2.1.2 直接网格算法(Grid-based Clustering)
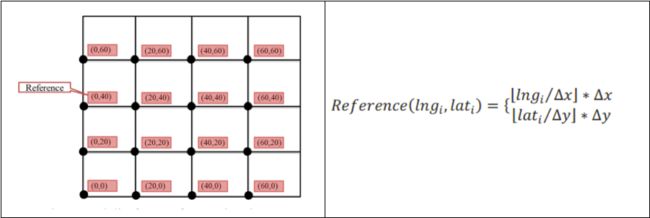
将地图划分为若干个网格,将落在对应网格中的点聚合在小网格的中心点。每个小网格只显示一个中心点,值为网格内的点数量。具体计算公式如下:
优点,运算速度快,不涉及两个点之间的距离计算,只有点是否处在网格内的一次性计算就能拿到结果。
缺点,如下图示,明明相近的两个点,因为划分在了不同的网格,而被迫分开计算在不同的网格中心。同时网格的中心,不一定就是网格内点的聚类中心,不能真实地反映聚类的中心点。
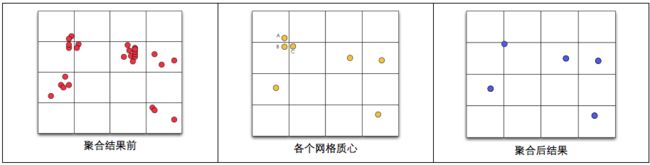
2.1.3 网格质心合并算法
与2.1.2方法基本一致,不同点在于,算法在将点划分到不同的网格中以后,会对每个网格的质心重新计算,得到更精确的聚类中心点。此外,还对经过质心计算的网格聚类中心点,进行了合并。(如果不进行合并,可能导致不同网格质心相近,造成覆盖)。网格质心的合并算法以一个网格质心为中心,画一个圆圈(或方格),将在这个范围内的网格质心都进行合并。圆圈或者方格的覆盖范围,可以作为配置来调整。
优点,运算速度较快(计算质心和合并质心不会带来特别大的计算量)
缺点,增加了计算量,同时也存在一定的误差,网格的划分,依旧可能会将原本聚集的点,强制分离开。
2.1.4 网格距离算法(Grid-Distance-based Clustering)
初始时没有任何已知聚合点,然后对每个点进行迭代,计算一个点的外包正方形,若此点的外包正方形与现有的聚合点的外包正方形不相交,则新建聚合点(这里不是计算点与点间的距离,而是计算一个点的外包正方形,正方形的边长由用户指定或程序设置一个默认值),若相交,则把该点聚合到该聚合点中,若点与多个已知的聚合点的外包正方形相交,则计算该点到到聚合点的距离,聚合到距离最近的聚合点中,如此循环,直到所有点都遍历完毕。
优点,运算速度相对较快,每个原始点只需计算一次,可能会有点与点距离计算,聚合点较精确的反映了所包含的原始点要素的位置信息。
缺点,速度不如完全基于网格的速度快等,同时各个点迭代顺序不同导致最终结果不同。因此涉及到制定迭代顺序的问题。同时聚类的中心点,是第一个加入该类的点的位置,并不能够代表整个聚类的中心位置,存在一定的不准确性。
2.1.5 四叉树算法(提供快速查找POI点的能力)+网格聚合算法(提供聚合POI点的具体策略)
首先明确,四叉树算法本身不提供数据聚合的能力,它的存在是为了配合之前的网格点聚合算法,提供快速查找到某一个网格下的所有POI数据的能力。
对应于二叉树,二叉查找树适合用来存储和查找一维数据,可以达到O(logn)的效率。在用二叉查找树进行插入数据时,查找一个数据只需要和树结点值的对比,选择二叉树的两个叉之一向下,直到叶子结点,查找时使用二分法也可以迅速找到需要的数据。对应于地图数据的二维坐标来说,四叉树可以很好地对二维数据进行存储和查找。它能够将数据分成四个象限,在查找数据时,通过对二维属性(一般是x, y)进行判断,选择四个分叉(象限)之一向下查找,直至叶子节点。(同样的对于三维数据来说,使用八叉树来进行存储和查询)。
2.2.5.1 四叉树的操作
节点分裂:
-
当满足特定条件时,为了获得更好的检索效率,四叉树的节点会发生分裂,分裂的做法是:以当前节点的矩形为中心,划分出四个等大的矩形,作为四个子节点,每个节点深度=当前节点深度+1,根节点深度为0;并且将当前节点的元素重新插入到对应的子节点。
插入元素:
-
从根节点开始,如果当前节点无子节点,将元素插入到当前节点。如果存在子节点(定义为K),并且元素能够完全被子节K点所“包围”,就将元素插入到子节点K,对于子节点K进行上述递归操作(即查看K节点是否有子节点,如没有子节点,则将数据存储在K节点上,如果有子节点,则下沉继续查找匹配);如果元素跨越了多个子节点,那就将元素存储在当前节点(即可以将跨越多个节点的数据存储在多个节点上)。
如果某一节点元素超过特定值,并且深度小于四叉树允许的最大深度,分裂当前节点。
查找元素:
-
对于给定检索区域,从根节点起,如果检索区域与当前节点有交集,且当前节点没有子节点,则返回当前节点的所有元素。
如果当前节点还有子节点,递归检索与检索区域有交集的子节点。
2.1.5.2 基于四叉树的点聚合方案具体实现:
采用网格质心算法来进行点的聚合,四叉树提供数据查询的能力。简单来说就是把屏幕分割成若干个区域,每个区域最多显示一个标注,每个区域的数据内容由四叉树来进行查询和提供。然后根据地图缩放比例去设置每个网格区域的大小以达到较好的展示效果。
使用基于四叉树的点聚合的方案首先需要建立四叉树,具体实现原理如下:
a. 首先对POI数据建立四叉树索引,四叉树的结构可以用如下代码表示。(创建四叉树的代价比较大)
typedef struct TBQuadTreeNodeData { //四叉树中存储的数据点(即poi信息)(一个四叉树节点可能包含多个数据点)
double x; //经纬度坐标
double y;
void* data; //额外的补充信息
} TBQuadTreeNodeData;
TBQuadTreeNodeData TBQuadTreeNodeDataMake(double x, double y, void* data);
typedef struct TBBoundingBox { //每个四叉树节点所表示的区间范围
double x0; double y0; //横纵坐标的最小值
double xf; double yf; //横纵坐标的最大值
} TBBoundingBox;
TBBoundingBox TBBoundingBoxMake(double x0, double y0, double xf, double yf);
typedef struct quadTreeNode { //四叉树节点
struct quadTreeNode* northWest; //西北象限(子节点)
struct quadTreeNode* northEast; //东北象限(子节点)
struct quadTreeNode* southWest; //
struct quadTreeNode* southEast; //
TBBoundingBox boundingBox; //本节点所表示的数据范围
int bucketCapacity; //本节点的数据容纳量(上限)
TBQuadTreeNodeData *points; //本节点存储的数据点信息(poi信息)
int count; //目前已经存储的数据点(poi点)个数
} TBQuadTreeNode;
TBQuadTreeNode* TBQuadTreeNodeMake(TBBoundingBox boundary, int bucketCapacity);
b. 建立四叉树的过程如下图所示,在到达节点的容量上限之后节点就会将其表达的数据范围从中心点开始划分为四个象限,构成它的四个子节点,子节点如果达到容量上限,同样重复这一过程。
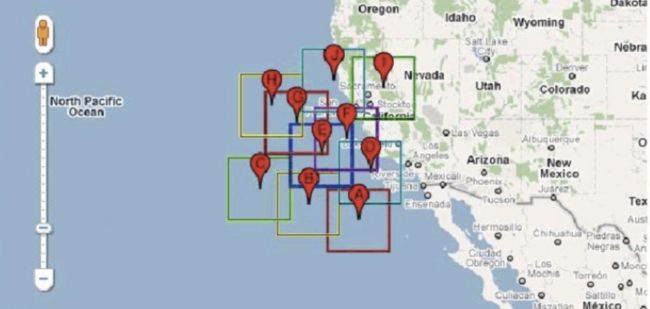
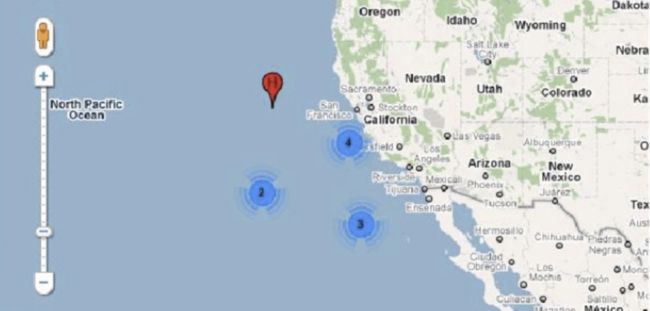
c. 查找一定范围内的POI数据的过程如下图所示(如下图中查找红色边框圈出来的范围)。比较红色区域是否和四叉树元素的根节点有交集,无交集则舍弃,有交集继续向四叉树的分支中进行查找。
2.四叉树建好并且能够进行区域查询。接下来点聚合算法就可以开始执行了,点聚合算法首先会先将当前屏幕划分为若干个网格(grid),然后对每一个网格通过四叉树来查找该网格内的POI,等找到同一个网格中的所有POI数据之后,计算其平均质心,并统计该网格中一共存在多少数据,即可完成聚合。
2.1.6 K-D树算法(同四叉树算法,提供快速查找的能力)
K-D树(k-dimensional树的简称)是一种分割k维数据空间的数据结构,主要应用于多维空间数据的搜索(如:范围搜索和最近邻搜索)。了解K-D树可以从理解线段树开始。
2.1.6.1 线段树的实现
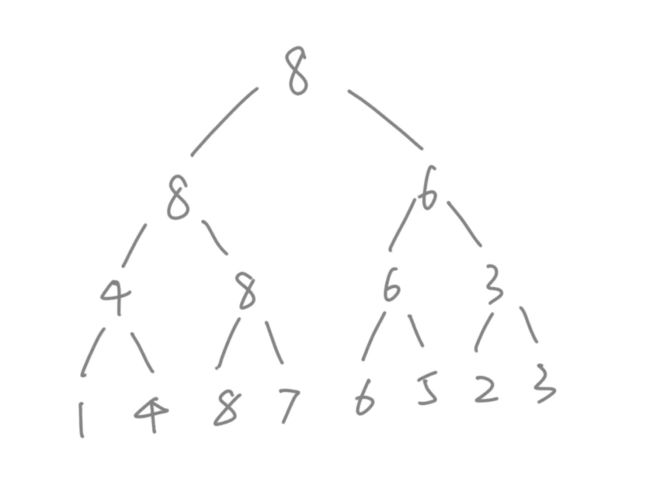
线段树的本质是一棵维护一段区间的平衡二叉树。线段树维护的是一个区间内的最大值。比如树根是8,维护的是整个区间的最大值,每一个中间节点的值都是以它为树根的子树中所有元素的最大值。其构建过程可以使用如下伪代码表示:
class Node:
def __init__(self, value, lchild, rchild):
self.value = value
self.lchild = lchild
self.rchild = rchild
def build(arr):
n = len(arr):
left, right = arr[: n//2], arr[n//2:]
lchild, rchild = self.build(left), self.build(right)
return Node(max(lchild.value, rchild.value), lchild, rchild)
通过线段树,可以在 O(logN) 的时间内计算出某一个连续区间的最大值。如下图所示:
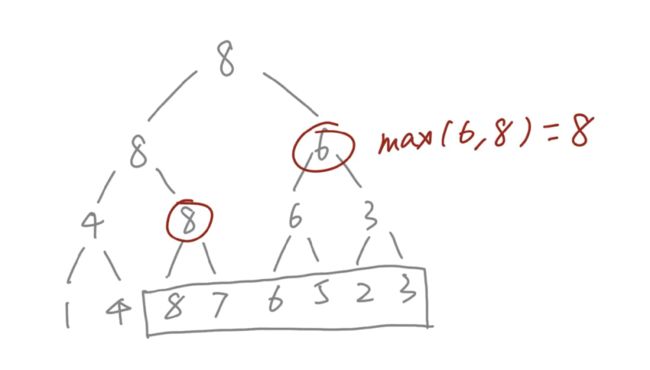
当需要查找树底层被方框圈起来的区间中的最大值时,我们只需要找到能够覆盖这个区间的中间节点就行。可以发现被红框框起来的两个节点的子树刚好覆盖这个区间,于是整个区间的最大值,就是这两个元素的最大值。这样,我们就把一个需要O(N)查找的问题降低成了O(logN),不但如此,也还可以做到O(logN)时间复杂度内的更新,也就是说不仅可以快速查询,还可以快速更新线段当中的元素。
2.1.6.2 K-D树的实现
线段树维护的是一个区间内的元素,是一个一维的序列。如果我们将数据的维度扩充一下,扩充到多维呢?KD-Tree就可以理解成是线段树拓展到多维空间当中的情况。以二维空间数据来说明K-D树如何建立。
K-D树建立过程
a. 一个二维的平面中分布着若干个点坐标。

b. 选择一个维度(比如选择X轴),将数据一分为二。
c. 经过切分之后,左右两侧的点被分成了两棵子树,对于这两个部分的数据来说我们更换一个维度在进行二分,(其实可以选择方差最大的维度进行划分,以此来保证更平均的分配,和更好的区分度)。此处我们选择y轴进行划分,就可以得到:
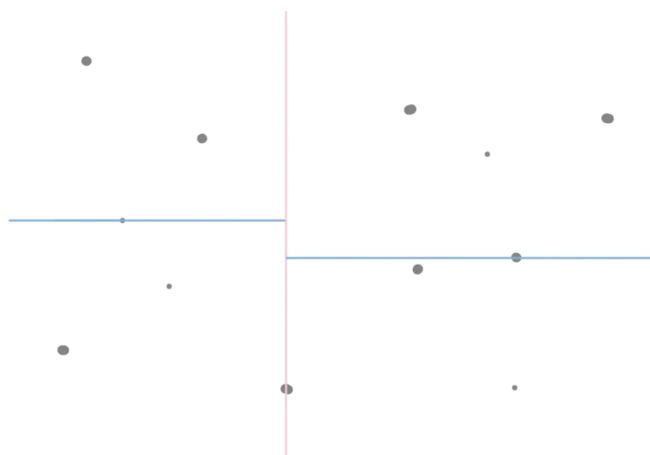
d. 重复上述过程,一直到点不能进行分割为止。即可得到一颗KD树。因为每次划分都是选择中位数来进行划分,所以可以保证根节点到叶子节点的深度不会超过log(N)。
最终建立的K-D树存储上的形式如下图所示: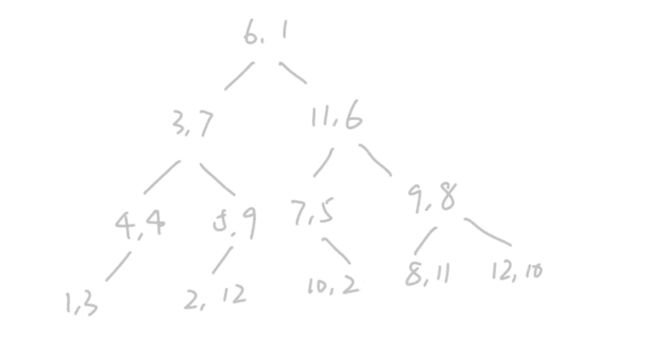
K-D树查询过程
K-D树的一个最大的优点在于,能够快速的进行批量查询,如查询K个距离最近的数据有哪些、查询距离满足一定阈值的数据有哪些等。
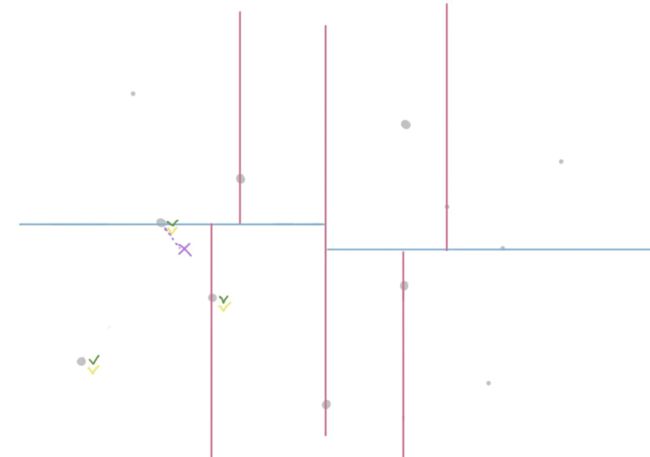
a. 假设我们要查找距离给定目标点最近的3个点。首先会创建一个候选集来存储答案。当找到叶子节点(叶子节点代表一块儿小区域)之后,这个区域当中只有一个点,把它加入候选集。如下图所示,“绿色✔️ ”表示样本被放入了候选集当中,“黄色✔️ ”表示已经访问过。
b. 通过判断样本和当前分割轴的距离,来确定分割轴的另一侧有没有更临近的数据点。
-
如果是叶子节点,没有轴的另一侧,则向上从父节点开始查找。
如果是非叶子节点,且当前候选集中已经存在K个最小值,则计算候选集中与目标点距离最远的距离(d2),与目标点到分割轴的距离(d1)谁更大:
-
如果目标点到分割轴的距离(d1)更大,即d1 > d2,则另一侧没有比候选集中距离(目标点)更小的点。不需要遍历另一侧的数据点。(因为另一侧距离目标点最近的距离,至少是目标点到分界轴的距离d1,还得加上另一侧到分界轴的距离x,即 d1+x > d2)。
如果目标点到分割周的距离(d1)更小,即d1 < d2,则分割轴的另一侧可能存在距离目标点更小的点,需要进行遍历。
(a步骤中的节点为叶子节点,本轮向上查找父节点,同时候选集中不满3个,父节点加入候选集)
c. 分析b步骤中的节点,虽然是父节点,但是另一侧没有数据,所以也向上查找他的父节点,同时目前候选集不满3个,也加入候选集。
d. 当前节点作为父节点,且右子节点不为空,所以需要判断目标点到分界线的距离,目标点到分界线的距离d1小于目标点到最远候选集中点的距离d2,所以分界线另一侧有可能有更小的值,需要遍历。
e. 找到边界另一侧的叶子节点,发现他到目标点距离,大于候选集到目标点的距离,同时候选集已经有了K个值,所以不能构成新的答案。需要继续向上查找他的父节点。
f. 发现其父节点到目标点的距离,比已有的候选集中的点更小,更新候选集。
2.2 点聚合实现方案:
依托于之前进行的调研,开始对点聚合方案进行实现。本文尝试了多种算法的实现,并就其性能和效果进行了对比。其中包含:
直接欧式距离算法
-
计算每个点,与周围点的距离是否在指定阈值之内,如果满足则共同构建聚合点,聚合点的坐标取平均值。
将步骤a中的聚合点,从原有数据集中剔除。重新从原始POI点中选择一个点,再次进行步骤a构建新的聚合点。
重复a,b两个过程,直至所有POI点都完成了聚合。
基于四叉树的直接欧式距离算法
-
与直接欧式距离算法基本一致,不同点在于,计算与周围点的距离是否在指定阈值之内时,是通过四叉树的查询来完成的。
网格质心算法
-
与3.1.2中算法基本一致,不同点在于,本算法计算了每个网格中数据点的平均质心作为聚合点的位置坐标。
网格质心合并聚合算法
-
在网格质心算法的基础上,新增了聚合点的合并逻辑,通过指定阈值来完成聚合点的合并。
基于四叉树的网格质心算法
-
与网格质心算法基本一致,不同点在于,查询一个网格内对应的数据时,使用的是四叉树来进行查询。
网格距离算法
-
与3.1.4中算法一致。
基于四叉树的网格距离算法
-
与3.1.4中算法基本一致,只是使用了聚合点来构建了四叉树,来加快遍历查询的速度。
基于KD树的网格距离算法
-
与3.1.4中算法基本一致,只是使用了聚合点来构建了KD树,来加快遍历查询的速度。
2.3 聚合算法流程:
算法的输入:
-
请求参数中需要包含data和config
-
data指的是需要聚合的poi数据,POI数据需要包含位置信息。
config指的是聚合算法的配置,如包含多少层级,每个层级聚合算法的相关参数等等。
算法的输出:
-
点聚合的结果数据中,包含了不同层级的点聚合结果,以Map < String, List < AggregationDTO > > 的形式下发,String代表不同聚合层级的唯一标识,List < AggregationDTO > > 代表着该层多个聚合点的数据。
每一层的聚合结果由多个聚合点来组成,其中每一个聚合点(AggregationDTO)需要包含如下信息:
-
聚合点的位置(经纬度或坐标)
聚合点包含的原始POI个数
其他信息(目前填充的是该聚合点聚合了哪些原始的poi数据信息)
整个算法的流程如下:
三、结果&效果
-
对于聚类结果的评价指标,核心的思想分为两部分:
-
一是紧凑度,即簇内样本距离尽量的近;
二是分离度,即簇与簇之间的样本尽量的远。
一篇谷歌学术引用量600+的论文做了解析,Liu Y, Li Z, Xiong H, et al. Understanding of internal clustering validation measures[C]//2010 IEEE International Conference on Data Mining. IEEE, 2010: 911-916. 结论是:一种“S_Dbw”聚类评价指标对于各种噪声,不同密度的数据集等等干扰项的评价结果鲁棒性最强,对比其他评价指标有显著优势。
“S_Dbw”公式分为两部分,Dens_bw(c)用来衡量各个类的平均密度关系,该值较小表明,聚类簇集的类间区分度较好。Scat(c)用来计算类内距离 ,距离越小同一类中数据对象间的相似性越高。具体公式中每个部分的解释可参考论文,此处不再赘述。
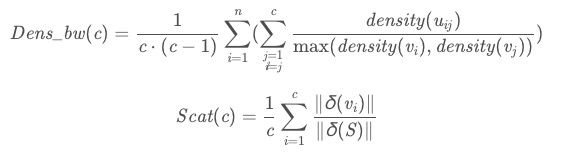
算法效果(部分算法直观演示)
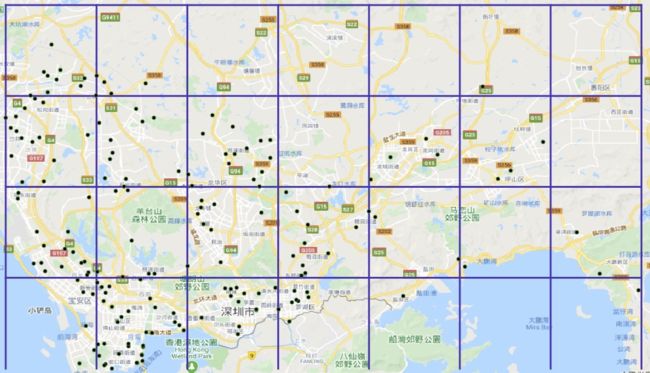
a. 网格质心算法(划分网格,然后计算每个网格的质心作为聚类中心)由于网格是固定的,出现了“聚集点被网格割裂”的情况。
b. 网格质心合并算法(在网格质心算法的基础上,对两个距离较近的聚合点,进行合并)
将点聚合的结果,再进行一次聚合,以期望被网格割裂开来的聚集点数据,能够重新聚合在一起。
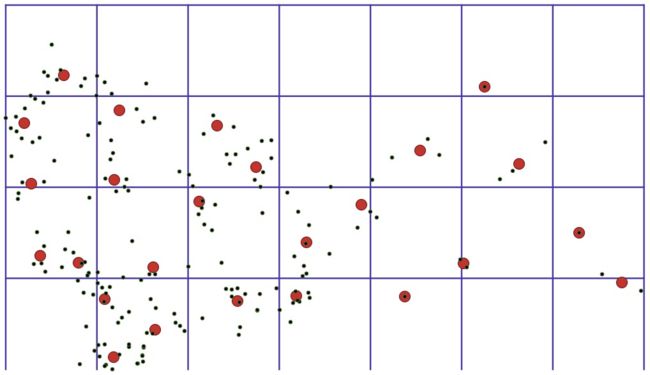
以原始数据点自身为中心,按照一定的距离范围,去聚合周围距离最近的聚合点。与其他算法不同,网格距离算法的设计思想是原始数据点和聚合点的合并,而不是原始数据点之间的相互合并。如果没有在聚合范围内找到聚合点,就以自身位置新建一个聚合点。
d. 效果对比:
-
在使用直接距离聚合算法和网格质心算法中,有些场景下会将距离较远的两个点聚合在一起,网格距离算法能够有效改善这种情况。原因有两个:
-
-
因为网格距离算法是将原始数据点聚合到“距离最近的”聚合点中,能够在一定程度上避免原始数据点聚合到“距离更远”的聚合点。
网格距离算法中,对于每一个原始数据点的遍历中,它能够影响的只有自己这一个原始数据点。而直接距离算法中每一个原始数据点的遍历,可能会影响到多个原始数据点。虽然两种算法都会受到原始数据点的遍历顺序影响,但影响的程度相差很大。总体来说,网格距离算法表现更好。
-
-
网格距离算法能够在一定程度上避免“网格将原本聚集的数据点割裂”开的这种情况。
-
-
如网格距离算法中所展示的两张图,聚合点的分布并没有被网格所局限。而对比网格质心算法所展示的效果图,其每个网格只能出现了一个聚合点。
-
不同算法使用建议:
 其中,原始POI数据量的大小分界线,以10K为分界线,超过10K可以认为数据量较大,算法之间的性能会有差别。聚合点数量的多少,以1K为边界,超过1K个聚合点可以认为聚合点数量较大。准确率和效率的要求,需要使用者根据业务的具体要求来做判断。
其中,原始POI数据量的大小分界线,以10K为分界线,超过10K可以认为数据量较大,算法之间的性能会有差别。聚合点数量的多少,以1K为边界,超过1K个聚合点可以认为聚合点数量较大。准确率和效率的要求,需要使用者根据业务的具体要求来做判断。
参考文献
[1]. 丁立国, 熊伟, 周斌. 专题图空间点聚合可视化算法研究[J]. 地理空间信息, 2017, 15(5): 6-9.
[2]. Theodore Calmes. How To Efficiently Display Large Amounts of Data on iOS Maps. https://thoughtbot.com/blog/how-to-handle-large-amounts-of-data-on-maps. 2015.
[3]. Liu Y, Li Z, Xiong H, et al. Understanding of internal clustering validation measures[C]//2010 IEEE International Conference on Data Mining. IEEE, 2010: 911-916.
[4]. 承志. 机器学习--详解KD-Tree原理. https://juejin.im/post/6844904117702246407, 2020.
[5]. Viky. 在线地图的点聚合算法及现状. http://www.doczj.com/doc/f5a88999284ac850ad0242a2.html, 2014.
招聘
阿里巴巴高德地图在线引擎和安全运维中心团队长期招聘机器学习算法、C++、Java 资深工程师/技术专家/高级专家,职位地点:北京。欢迎投递简历到 [email protected],邮件主题为:姓名-应聘团队-应聘方向。
![]()