斯坦福学霸理论验证:自学习如何避免使用伪特征?
点击蓝字
![]()
关注我们
AI TIME欢迎每一位AI爱好者的加入!
在无监督域自适应中,现有理论着眼于源域和目标域接近的情况。在实践中,即使源域和目标域差别很大,自训练算法也通常很成功。我们分析较大域偏移的一种情况:某些伪特征与源域中的标签相关,但与目标中的标签无关。我们考虑线性模型,伪特征是高斯分布。我们证明了:如果使用相对准确的源模型,自训练在数据分布变化时避免使用伪特征。我们在Celeb-A和MNIST数据集上验证了该理论。我们的结果表明,在标注很难获得的时候,从业人员可以在大型多样无标注的数据集上进行自训练,以提高模型准确性。
陈怡宁:本科毕业于达特茅斯大学计算机和哲学系,现为斯坦福大学计算机系的博士生,导师为马腾宇。主要研究兴趣是机器学习和深度学习理论,尤其是转化学习,无监督和半监督学习,以及在数据分布发生变化时,如何提高模型正确性。
![]()
一、背景:无监督域适应
人工智能模型经常遇到一个问题:训练和测试数据分布不同时,模型的正确率往往会下降。举个例子,假如我们要设计一个自动驾驶系统,训练数据集都是在某种天气条件下收集到的,但测试的时候,也就是运用模型的时候,会遇到各种各样的天气,比如晴天、雨天、雾天。由于数据分布发生变化,模型的正确率往往会下降,表现极不稳定。
那么,如何构造一个更加稳定的模型?如何在无监督的情况下进行域适应(unsupervised domain adaptation)?
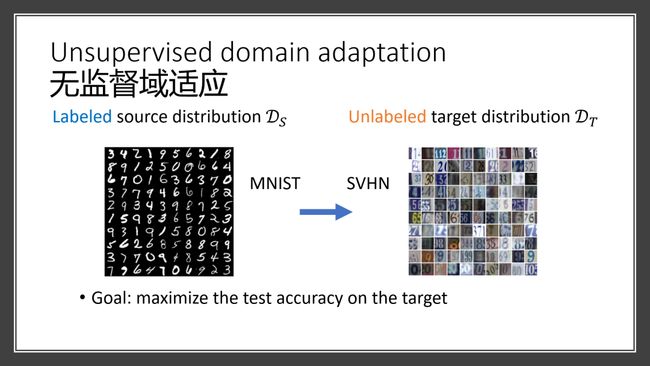
这种情况下,源领域的数据都有标记,而目标域的数据则无标记。例如在有标记的MNIST数据集和无标记的SVHN数据集上识别数字,MNIST是黑白手写数字,而SVHN则是颜色各异的门牌号码,两者数据分布显然不同。如何在无监督的情况下,在目标域上得到最高的准确性?
现有文献大多会假设两种数据比较接近,这其实不符合现实情况。在刚刚的例子中, MNIST和SVHN事实上没有交集,能够很明显地看出任何一个MNIST的数据都不是SVHN的数据点。
尽管很多现实问题中使用的自学习算法(self-training algorithms)效果很好,但现有理论并不能解释为什么这些算法在源域和目标域相差很大时仍能得到较好的效果。因此,我们希望从理论上研究两种应用普遍的自学习算法——伪标记算法和熵减算法,给出适用和不适用的条件,从而建立域适应的理论。
二、证明:域适应理论
我们假设目标域比源域更加多样化,在此之上证明自学习算法能提高目标域上的准确性。
假设输入的特征分为两种,其中x1代表含有信号的特征,而x2代表伪特征。信号特征(signal features)无论在哪个领域都决定了标记,而伪特征(spurious features)在源领域中和标记有联系,但在目标域中和标记毫无联系。
举个例子,目标是判断图像中动物的种类,那么图片的前景往往是信号特征,而图片的背景往往是一些伪特征。比如在某个特殊的数据集里,大多数鸟的背景是水,但在目标域中背景变成蓝天。这种情况下,如果我们使用了伪特征,在目标域上表现就不是很好,而如果使用前景这个信号特征的话,在目标域上的表现就不会变差。
我们分析的模型是线性模型。
这两个算法其实非常接近,一开始都是在有标记的源领域上训练模型,称作ws。图中左边是伪标记算法,用ws作为老师模型,用来标记目标域中没有标记的数据,从而产生一些伪标记。然后在这些伪标记上训练学生模型,并比较学生模型和老师模型的表现。
在熵减算法中,我们对ws模型进行微调,目标是降低预测在目标领域上的熵。换句话说,我们希望在目标域数据上的预测更有信心。
我们的论文证明,这两种算法虽看似不同,实则非常相似。
核心结论是:假设信号特征x1满足某种数据分布,伪特征x2是正态分布。假如在源领域得到的模型还不错,没有完全依赖伪特征,那么在没有标注的目标域上进行自学习,会得到一个并没有使用伪特征的新模型,而我们只需要多项式数量的、没有标记的目标领域的数据来完成。
下图能够直观展示我们的算法到底在做什么。图中横轴是信号特征,纵轴是伪特征。假设我们有两个类,分别以圆形和三角形表示,方框则表示类别不明的未标注数据。如果在源领域上训练,会得到图中绿色虚线所示的模型。如果在目标域上进行自训练,会得到红色的垂直虚线。这条虚线相比绿色虚线在目标域上有更高的准确性,并且由于是垂直的,完全不用伪特征。在这种简单的情况下,它就是目标域上的最优解。
2.1 证明思路
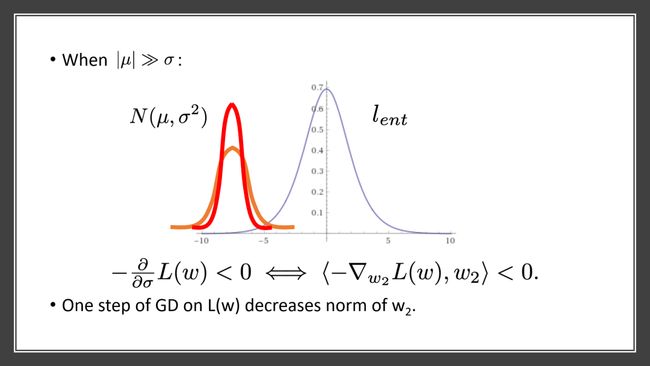
因为我们关注的是线性模型,所以可以把该模型分为信号特征x1上的权重w1和伪特征x2上的权重w2,我们的预测是w⊤x也就是w1⊤ x1加上w2⊤x2,这实际上是高斯分布,因为我们假设固定x1后,x2是高斯分布,所以预测也会是高斯分布。该分布的mean由w1和x2决定,而 variance由伪特征和伪特征的权重决定。我们可以把单个数据点上的损失函数写成如下公式,通过调整参数写成关于μ和σ的函数方程。
由于损失函数形状是蓝色曲线,如果想减少损失,我们会尽量使预测远离原点,即更正或更负的方向。橙色曲线是w⊤x的分布,由于是正态分布,有mean和variance。我们的目标是减少损失,尤其关注减少损失对于variance(σ2)的影响,因为σ2关系到伪特征的权重。其实如果要减少损失,我们会让预测更加集中,即σ更小,这也就导致w2会变小。由此证明了一步的梯度下降后,对于伪特征x2的依赖也会下降。
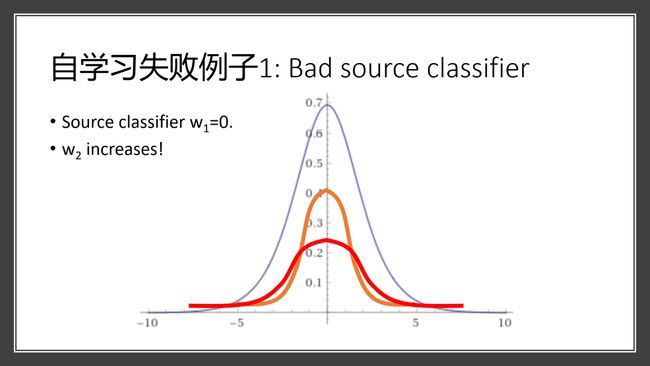
我们的理论也说明自学习并不总会成功,比如有一些自学习失败的例子。第一个例子是,假如在源领域上得到的模型非常糟糕,完全不使用信号特征,而完全依赖于伪特征。假如我们现在想减少蓝色的loss,那么实际上要让预测更加远离原点,也就是分布变得更宽。这种情况下,伪特征的权重w2其实是会增加的,自学习也就会失败,所以我们必须要有一个较好的源领域上的模型,才能使学习成功。
自学习失败的第二个例子中,如图还是w⊤x的分布,有两个部分离原点非常远,有一个部分离原点非常近。离远点很远的两个部分mass很大,而靠原点很近的部分mass很小,所以源领域一开始的模型准确率已经非常高了。但是在这种情况下,自学习还是会增加对于伪特征的权重,为什么会这样?因为左右两个部分虽然是想让权重变得更小,但对于loss function的贡献非常小,而中间部分对于loss function的贡献非常大,所以总的作用是使得w2增长。
所以,要让自学习成功,我们必须对信号特征x1做出假设,来避免出现图中的情况。
我们的理论中对于x1如是假设:它是sliced log-concave和sliced log-smooth distribution,并且如果信号特征较强、各个类别分得较开、噪音较小的情况下,这些条件都是满足的,自学习也就能发挥作用。
2.2 实验验证
为了验证我们的理论,进行了两个实验。
第一个实验是用 MNIST数据集,目标是数字识别。我们设计了一个源域,其中越大的数字颜色越红,数字越小则越绿。在目标域里,所有数字都有一个随机的颜色,图像的形状是信号特征,颜色是伪特征。在源域中,伪特征和目标有很大联系,而在目标域中并没有这样的联系。
第二个数据集是celebrity data set,目标是识别人脸的性别。在源领域里,男性都是浅色头发,女性都是深色头发。目标域是原数据的一个随机子集,所以两个性别的人都有各种各样的头发颜色,这也就符合我们之前的假定:目标领域的数据要更加多样化。
实验结果证明,自学习能够提高目标域的正确率。表中,我们可以看到大部分的情况下,自学习后模型的准确率都会上升,但是最后一列准确率反而有所下降,这也和我们的理论是吻合的:如果在源领域上模型表现不是很好,即完全依赖于伪特征,那么自学习会使得于伪特征的依赖增强,因此在目标域上表现更差。
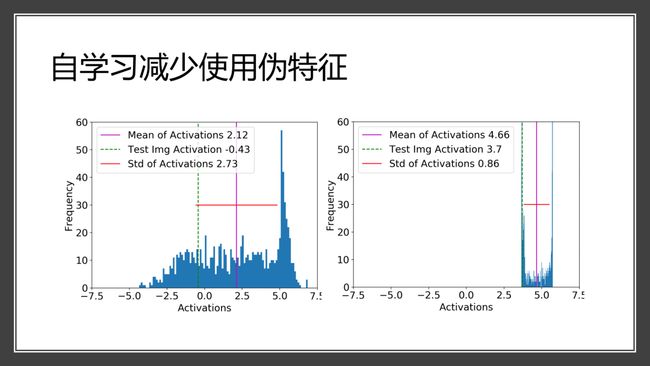
实验也验证了自学习能减少使用伪特征,下图是colored MNIST dataset上的预测,左边是自学习之前,右边是自学习之后。当我们固定图像形状、改变颜色后,可以看到左边分布较宽、有正有负(正的是正确预测,负的是错误预测),自学习后右边分布明显变窄、并且非常集中,所有预测都为正。因此,自学习减少了对于颜色的依赖,并使得正确率有所提高。
在celeb dataset上,我们随机选取了一些原数据集上模型预测错误,但自学习把它更正的例子,可以看到大部分都是浅色头发的女性或者深色头发的男性。这些例子原来之所以会被预测错,是因为源域上的模型使用了头发颜色作为伪特征进行自学习,因此减少使用伪特征就能正确判断这些例子。
总结
我们的工作从理论上证明了当源领域存在伪特征、但目标领域没有的时候,自学习能利用没有标注的目标数据来减少对伪特征的依赖。
并且,我们给出了自学习成功的条件,比如目标信号特征较强、没有噪音、有较好的源领域模型,结论和最近一些大型的实验性的半监督学习研究非常吻合。
论文链接:
https://arxiv.org/pdf/2006.10032.pdf
整理:鸽 鸽
审稿:陈怡宁
排版:岳白雪
AI TIME欢迎AI领域学者投稿,期待大家剖析学科历史发展和前沿技术。针对热门话题,我们将邀请专家一起论道。同时,我们也长期招募优质的撰稿人,顶级的平台需要顶级的你!
请将简历等信息发至[email protected]!
微信联系:AITIME_HY
AI TIME是清华大学计算机系一群关注人工智能发展,并有思想情怀的青年学者们创办的圈子,旨在发扬科学思辨精神,邀请各界人士对人工智能理论、算法、场景、应用的本质问题进行探索,加强思想碰撞,打造一个知识分享的聚集地。
![]()
更多资讯请扫码关注
![]()
(直播回放:https://b23.tv/6feVqX)
(点击“阅读原文”下载本次报告ppt)