入门--matplotlib绘图及进阶

matplotlib 绘图及进阶

（写在前面：作为一名初出茅庐的菜鸡，我尽可能以一种专业的角度‘严肃地写下这篇博文，Let’s 冲冲冲！）
码农们你可知 matplotlib 是python最伟大的绘图库，下面让我们一览她冰山一角的风姿

初等绘图

我们首先学习画一些基本的图吧：
1.描点
二话不说亮代码：

import matplotlib.pyplot as plt
#几乎是广大码农的习惯写法了，这里沿用
x=[0, 30, 60, 90, 120, 150, 180, 210, 240, 270, 300, 330, 360]
y = [0, 0.5, 0.866, 1, 0.866, 0.5, 0,-0.5, -0.866, -1, -0.866, -0.5, 0]
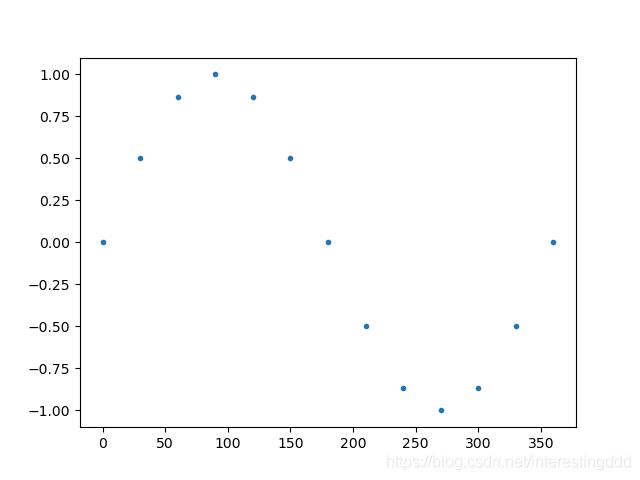
plt.plot(x,y,'.')
plt.show()
#将图像显示出来，类比于 print()

输出：

可见这里输出了一个周期下的正弦曲线点图，就是好稀疏，没事，我们一点一点来，我想先解析一下上面的码码，第一行是你使用 matplotlib 的常规操作，注意我们这里仅使用了 pyplot,所谓的 pyplot 是我们用 python 绘图的贴身朋友，与MATLAB（玩数学建模的盆友不陌生吧）类似，她有许多的有关绘图的函数，接下来的讲解与其说是 matplotlib 绘图，不如说是 pyplot 绘图，让我们·在接下来的探索中慢慢感受她的魅力，好，接下来我们傻乎乎地手动创建了点的横纵坐标的列表，进而 plt.plot(…),我们调用她进行二维图像的绘制操作，这里我们包含了横纵坐标以及引号内的点，它控制显示样式是点，另外还可以控制颜色，比如我们改进一下：

import matplotlib.pyplot as plt
#几乎是广大码农的习惯写法了，这里沿用
x=[0, 30, 60, 90, 120, 150, 180, 210, 240, 270, 300, 330, 360]
y = [0, 0.5, 0.866, 1, 0.866, 0.5, 0,-0.5, -0.866, -1, -0.866, -0.5, 0]
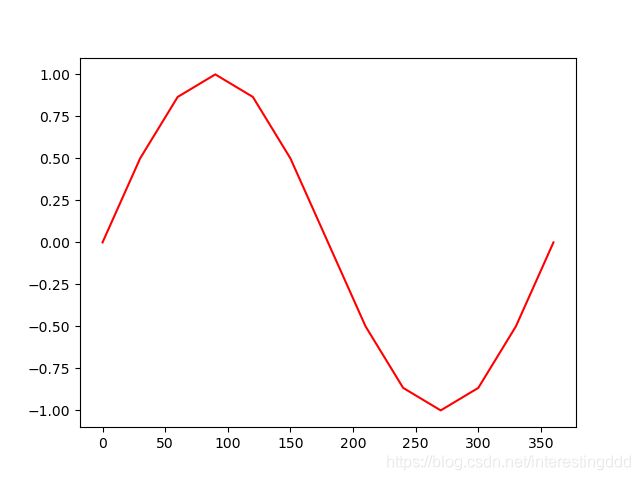
plt.plot(x,y,'r-')
plt.show()

奇怪的事情发生了：

啊这，好丑，可见 plot 让我们在输出样式上恣意妄为，下面是一些常用的颜色与样式：
color（默认蓝色）：

更多的颜色表示可以上网查找，接下来是输出的样式：
’-‘ : 实线
’- -‘: 虚线
‘-.’: 一线一点
': ’ : 密集点（可以用来改进上述的代码输出）
‘.’ : 绘制点图
‘o’ : 圆（比点显得更大）
‘*’ : 星号
‘+’ : 加号
‘|’ : 局部竖线
‘_’ : 局部横线
‘s’ : 局部方块（square）
. . . . . .
我们发现，上述代码对横纵坐标采样时点过于稀疏了，而要更密集就大大加大了工作量，可能有朋友要骂我不会变通了，哈哈哈，我们要相信 python 的功能强大，只要你对她了解得比自己的女朋友还清楚，虽然俺没有。。。这里我们先借助列表以及 math 库解决数据的输出问题，兄弟们，亮剑！：

import matplotlib.pyplot as plt
from math import *
#同时调用math库中所有的函数，用起来比较方便
x = range(0, 360)
##缺省值是1，也就是默认的间隔为1
y = [sin(radians(e)) for e in x]
#这里利用了生成一个与列表 x 相关的一个新的列表的紧凑方式，让你的代码简洁漂亮
plt.plot(x, y, 'co')
plt.grid('on')
#表示显示网格（如图）
plt.show()

输出:

很接近了吧，一些说明我直接写在注释里了，在这里我只想强调一下调用三角函数是一定要注意是否已经转化为了弧度（ radians( ) ),三角函数只计算弧度哦，而我们一般先定义一个新的函数再进行调用，大大提高了其通用价值，这里给出心形线，送女友说不定就成了哟~~：

import numpy as np
#数组库，比列表的功能更加强大
import matplotlib.pyplot as plt
def loveyou(YOU,I):
    t = np.linspace(0, 2*np.pi, 100)
    # np.linspace() 类比于列表的 range(),它有三个参数，左闭右开，最后一个是将这个区间等分成几份
    y =YOU*np.cos(t)-5*np.cos(2*t)-2*np.cos(3*t)-np.cos(4*t) #求n个y
    x =I*np.sin(t)**3   #求n个x
    #心形线函数，查数学资料吧哈哈哈，这里注意强大的 numpy 库也有一套数学运算符号，只是加上了前缀 np.sin()...
    love=[x,y]
    return love
plt.plot(loveyou(13,14)[0],loveyou(13,14)[1], 'm-') #绘制
#这里我用列表储存两个返回值
plt.axis([-25, 25, -20, 15])
#限制坐标值的范围，参数是（[x左,x右,y左,y右]），都是左开右闭
plt.show()

抓紧看看输出了啥：

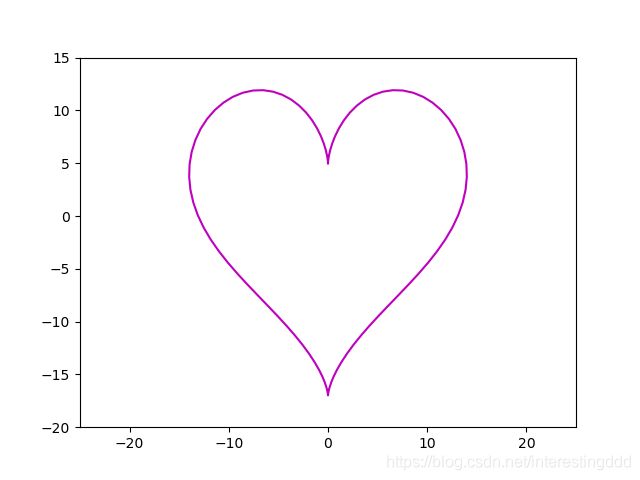
还可以，我的水平有限，大家可以发挥创造性自由发挥给出更多的想法哦，这里也就是说，绘图数据的来源还可以用 numpy 产生，numpy 的强大也有带我们慢慢体会…
将正弦函数代码改成线形样式也许更加舒服：

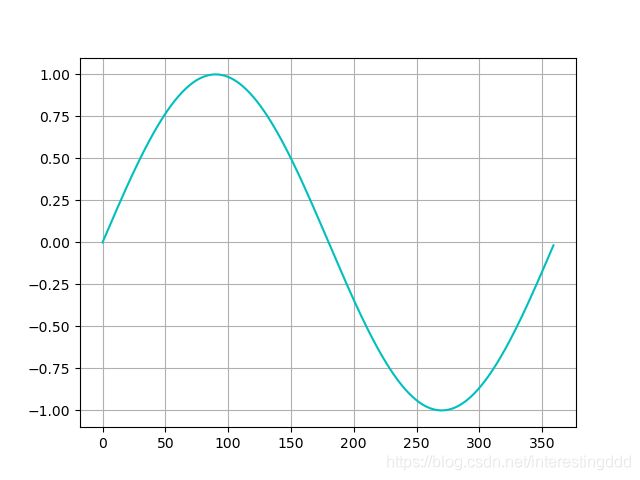
十分接近了，这里我只是将 ’ co ‘改为’ c- '而已
那么，在一张图中绘制多条曲线呢？很简单，只需要定义两个不同的 y 就好了：

import matplotlib.pyplot as plt
from math import sin, cos, radians
x = range(0, 360)
y1 = [sin(radians(e)) for e in x]
y2 = [cos(radians(e)) for e in x]
plt.plot(x, y1, 'b-' )
plt.plot(x, y2, 'y:')
plt.show()

输出：

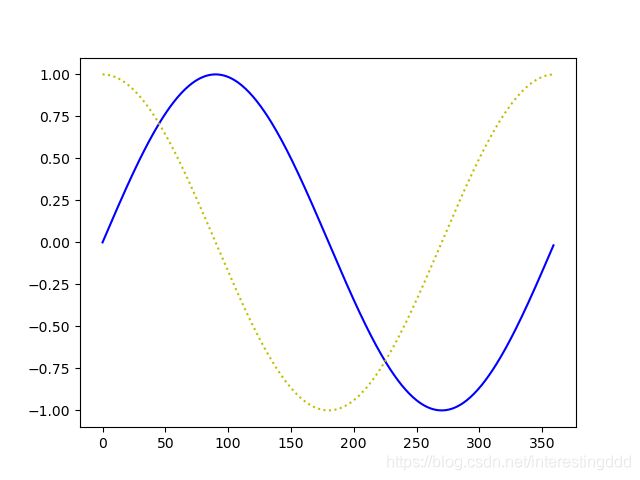
To be continued…
#####################################################
1月15日
灵机一动，既然我们有画图工具在手了，那么我们可以结合数学知识画图娱乐了，那我现在就随机画一个玩玩：

import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif']=['SimHei']
#用 plt.rcParam 设置显示中文
plt.rcParams['axes.unicode_minus'] = False
#同上，设置正常显示字符，这里是负号，否则输出可爱的小方框
x=np.linspace(-3.14,3.14,6280)
y=5*np.sin(x)*np.cos(x)/np.exp(2*x)
#瞎编一个函数
plt.plot(x,y,'c-')
plt.rcParams.update({
     'font.size': 10})
#设置图例大小，包括边框
#plt.legend('曲线',loc='upper center')
#这里我为什么注释掉了呢？我听了某位博主的介绍，说将 plt.legend() 放在plt.show() 之前就能正常输出中文，而我试了一下不行，输出见图，可见博主的介绍也有真伪性哈
plt.xlabel('x轴')
plt.ylabel('y轴')
#设置坐标轴的标签，效果见图
plt.axis([-4,4,-100,500])
plt.grid(True)
#显示网格的另一种方法
plt.legend('曲线',loc='upper center')
#显示图例，问题出在这里，为啥只有一个字哈哈哈哈？？
plt.show()

啊，玩出来一个问题哈哈哈，卡了一会也没有解决，输出这样：

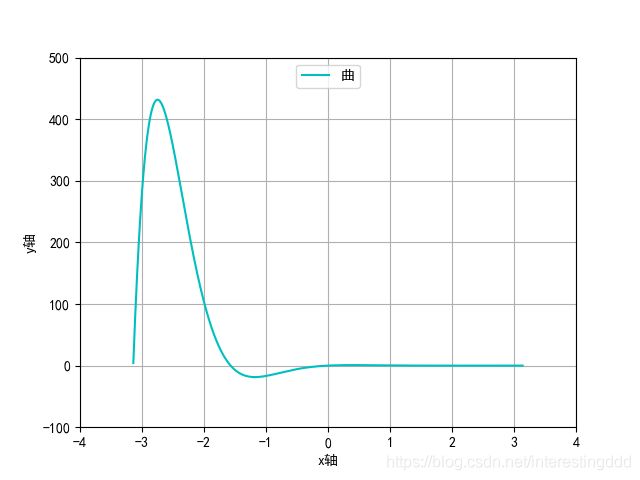
观察到了吗？这里加了一些操作哦，不着急，一些讲解仍然放在注释中，这里注释出现了问题，请教了别人，原来应该用 ['曲线‘] 问题得到解决，输出：

完美是不是？顺便提一句，图例一般用在多线共图中，要用列表表示，比如：[‘apple’,‘banana’,…],注意控制顺序与绘图的顺序一致以使图例与图线一致，举上面的例子：

import matplotlib.pyplot as plt
from math import sin, cos, radians
x = range(0, 360)
y1 = [sin(radians(e)) for e in x]
y2 = [cos(radians(e)) for e in x]
plt.plot(x, y1, 'b-' )
plt.plot(x, y2, 'y:')
plt.legend(['cos(x)','sin(x)'],loc='upper center')
plt.show()

输出：

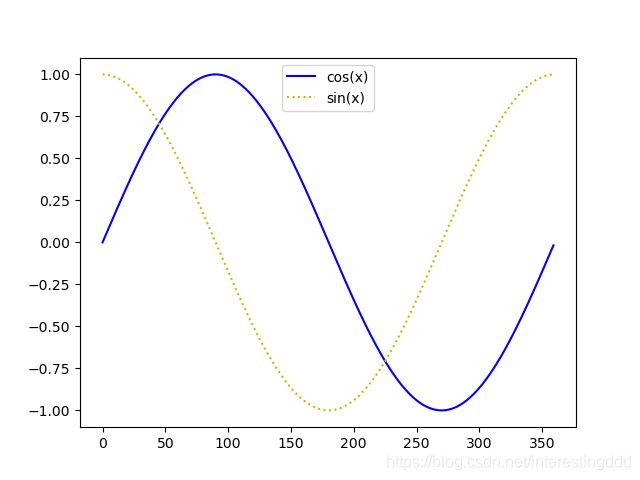
可见改变了顺序就事与愿违了！
接下来绘制柱状图：
1月21日，我终于来绘制柱状图啦~我不懒哦，这几天发了其它的几篇文章，交叉着来可以让记忆更深刻，我坚信这一点，所以我尽量是多个方面交叉着来做，开始开始！：
事先声明，这里只讲简单的柱状图哦，等我放寒假了再逐步进阶补充，这里的知识点好多好多的，我现在还有学业，先不深入了，朋友们理解一下哈：

#数据：
xstring = '2015年 2014年 2013年 2012年 2011年 2010年 2009年 2008年 2007年 2006年 2005年 2004年 2003年 2002年
ystring='25 65 85 41 65 2 52 95 30 52 87 43 10 28'

下面绘制柱状图：

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
#使‘年’正常显示，否则又是方框乱码哦
xstring = '2015年 2014年 2013年 2012年 2011年 2010年 2009年 2008年 2007年 2006年 2005年 2004年 2003年 2002年'
ystring='25 65 85 41 65 2 52 95 30 52 87 43 10 28'
y=[float(i) for i in ystring.split()]
#别忘了将字符串转换为浮点数之后才能作为纵坐标的数据
y.reverse()
#按照习惯，我们绘制柱状图时时间从左往右流逝
xlabels=xstring.split()[::-1]
#别忘了横坐标数据一起倒序哦，不然数据与年份对不上号了，这里两种倒序方式就都全啦
x=range(len(xlabels))
plt.xticks(x,xlabels,rotation=45)
#这里的 xticks() 函数用来设置 x 轴，每一个对应位置的 x 显示一个对应标签，倾斜角度为45度
plt.bar(x,y,color='m')
#类比于 plot(),柱状图用 bar()
plt.show()

输出：

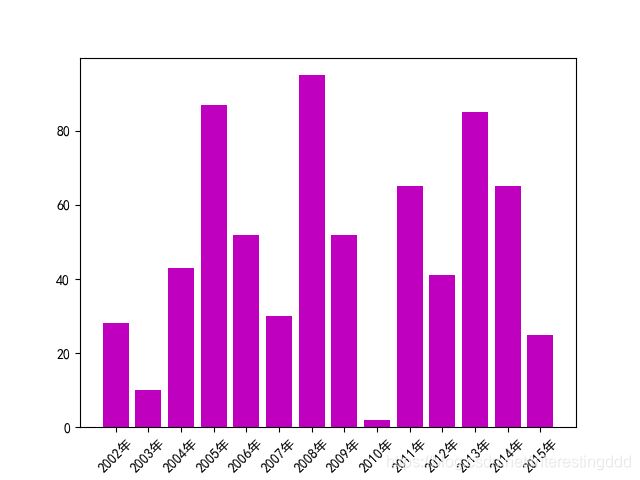
这样我们就绘制出了第一个柱状图，下面绘制两个试试吧：

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
xstring = '2015年 2014年 2013年 2012年 2011年 2010年 2009年 2008年 2007年 2006年 2005年 2004年 2003年 2002年'
ystring1='25 65 85 41 65 2 52 95 30 52 87 43 10 28'
ystring2='52 85 63 3 4 96 85 75 21 85 96 34 94 52'
y1=[float(i) for i in ystring1.split()]
y2=[float(i) for i in ystring2.split()]
y1.reverse()
y2=y2[::-1]
#两种倒序的方法
xlabels=xstring.split()[::-1]
x=range(len(xlabels))
plt.xticks(x,xlabels,rotation=45)
plt.bar(x,y1,color='m')
plt.bar(x,y2,color='c')
plt.xlabel('年份')
plt.ylabel('两组数据')
plt.grid('on')
plt.legend(['数据1','数据2'],loc='upper right')
plt.show()

输出：

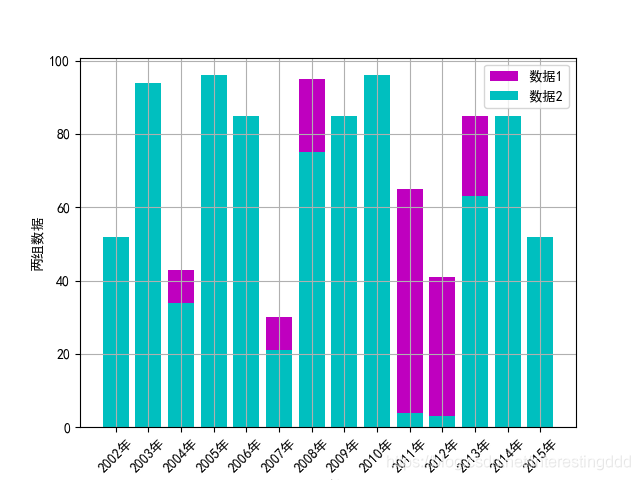
用的都是之前讲过的知识点，就不多解释了，但是。。这个输出重合了就很烦人，这里我们需要控制两个柱的横坐标不同才能将它们分开：

import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif']=['SimHei']
xstring = '2015年 2014年 2013年 2012年 2011年 2010年 2009年 2008年 2007年 2006年 2005年 2004年 2003年 2002年'
ystring1='25 65 85 41 65 2 52 95 30 52 87 43 10 28'
ystring2='52 85 63 3 4 96 85 75 21 85 96 34 94 52'
y1=[float(i) for i in ystring1.split()]
y2=[float(i) for i in ystring2.split()]
y1.reverse()
y2=y2[::-1]
xlabels=xstring.split()[::-1]
x=np.arange(len(xlabels))
plt.xticks(2*x+0.5,xlabels,rotation=45)
#控制 x 对应的那个小竖杠在两个柱子之间，更加美观
plt.bar(2*x,y1,color='m')
plt.bar(2*x+1,y2,color='c')
#分开两个柱子的位置，注意横坐标都乘以 2 了呦
plt.axis([-1,2*len(x),0,100])
plt.xlabel('年份')
plt.ylabel('两组数据')
plt.title('柱状图')
plt.grid('on')
plt.legend(['数据1','数据2'],loc='upper right')
plt.show()

输出：

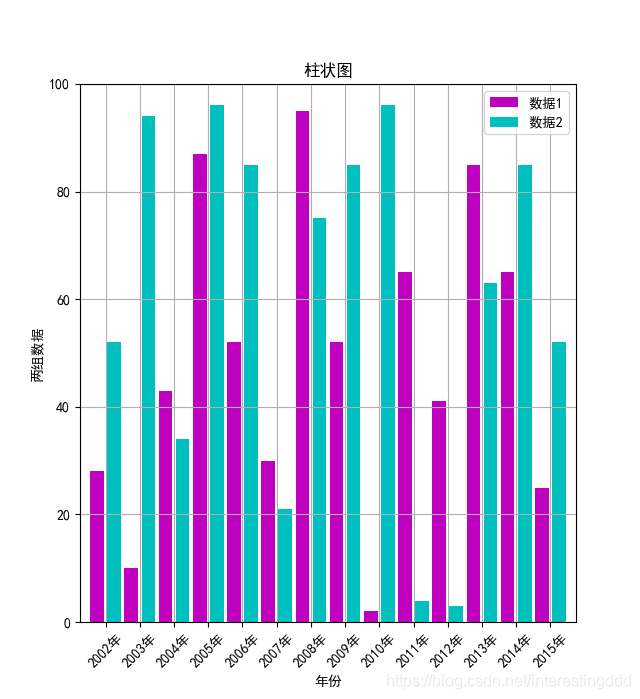
这样做虽然分开了柱子，但是同一年的数据仍然显示得不太清晰，我们继续改进，这里我们在画柱子时设置合理的宽度，使得同一年的柱子靠在一起，区分度高了许多，nice:

import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif']=['SimHei']
xstring = '2015年 2014年 2013年 2012年 2011年 2010年 2009年 2008年 2007年 2006年 2005年 2004年 2003年 2002年'
ystring1='25 65 85 41 65 2 52 95 30 52 87 43 10 28'
ystring2='52 85 63 3 4 96 85 75 21 85 96 34 94 52'
y1=[float(i) for i in ystring1.split()]
y2=[float(i) for i in ystring2.split()]
y1.reverse()
y2=y2[::-1]
xlabels=xstring.split()[::-1]
x=np.arange(len(xlabels))
w=0.9
#设置成 1 会连成一片
plt.xticks(2*x+w/2,xlabels,rotation=45)
plt.bar(2*x,y1,width=w,color='m')
plt.bar(2*x+w,y2,width=w,color='c')
plt.axis([-1,2*len(x),0,100])
plt.xlabel('年份')
plt.ylabel('两组数据')
plt.title('柱状图')
plt.grid('on')
plt.legend(['数据1','数据2'],loc='upper right')
plt.show()

输出：

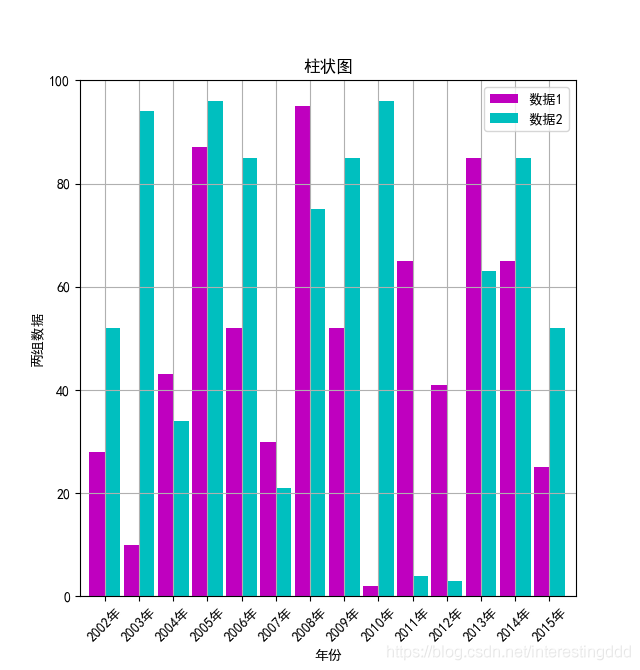
这样两个柱子就画好啦~你学废了吗？寒假后继续更新哦（1月29日后。。）
To be continued…

数组–Numpy，从入门到 TOMB

简单插入一段numpy讲解，开淦：
呜呜呜呜~我是一个苦逼的大学生，这两天不能玩手机了，博文是我最好的朋友了，多写写吧，起码我多学了好多，何乐而不为呢哈哈哈，开始吧兄弟萌：
numpy 是针对多维数组的扩展包，老规矩，下面我直接借助代码简单介绍一些函数及内置用法：

import numpy as np
a=np.array([[1,2,3],[4,5,6]])
print(a)
#返回对应的数组
print(a.shape)
#以元组的形式返回a 的行数与列数
print(a.size)
#返回a的元素的个数
print(a.itemsize)
#返回a的元素所占的字节数
print(a.ndim)
#返回a的维数，也就是有几层方括号
print(a.dtype)
#返回a的元素的类型
print(a[1,2])
#返回a的对应位置的元素，当然从0开始
print(a[1,:])
#这里返回第二层位置为一的数组
print(a[1,1:2])
#这是一个小坑，这里返回a[1,1],因为是左闭右开
a[1,:]=[7,8,9]
print(a)
#这里改变了a的对应的元素
b=np.array([[1,2,3],[4,5,6]])
print(a+b)
print(a-b)
print(a*2)
print((a*2)*(b*2))
print(b/(a*2))
print((a*2)**4)
print(a.sum())
#上述的运算只限同型的数组，也就是行数和列数相等，热而且运算都只是单纯的对应位置做相应的运算，不同位置之间没有相互影响
print(np.max(a))
print(np.min(a))
#返回最大最小项
d=a
d[0,1]=0
c=a.copy()
c[0,1]=0
print(a)
print(d)
print(c)
#这里的输出与你的预期一样吗？输出的a,b,c是完全一样的，关键在于我们要知道 a 与 d 没有什么差别，用不太专业的话说，它们指向同一个储存空间，所以无论你用哪一个变量值作元素变化另一个变量也随之改变了！而浅拷贝出的 c 的变化不影响 a 哦

a=np.zeros((5,2))
print(a)
#返回5行2列的元素全为0的数组
b=np.ones((2,5))
print(b)
#同上，2行5列，元素为1
c=np.empty((3,2))
print(c)
#个人认为这东西比较无聊，它默认输出 float64 类型的3维2列的数组，元素值竟然是我上面的 print(b/(a*2)) 的 reshanpe!? （有知道为什么的大佬吗？？）神奇！！
d=np.identity(3)
#输出相应维数的单位方阵
e=np.eye(2,3,k=1)
f=np.eye(3,2,k=0)
#输出2行3列的'对角阵',k=0类似主对角，正数为高对角，负数反之，参照输出结果理解
print(d)
print(e)
print(f)

a=np.random.random((4,2))
print(a)
#这个比较好玩，返回（0，1）之间任意的数组成4行2列数组，注意两次 random

a=np.arange(2,63,5)
print(a)
#指定步长输出，类比列表的 range，左闭右开
b=np.linspace(2,62,13)
print(b)
#输出指定元素个数，这是个罕见的闭区间！！这里等价于步长为5分12份

哇，好长是不是，都是一些干货知识点，多用用就熟啦，讲解仍然放在代码注释中了，阅读愉快哈哈哈。。
输出：

[[1 2 3] 
 [4 5 6]]
(2, 3)  #行列数
6       #元素数
4       #元素所占的字节数
2       #维数
int32   #元素类型
6       #相应位置元素
[4 5 6] 
[5]     		#这里输出了一个元素的数组
[[1 2 3]		
 [7 8 9]]
[[ 2  4  6]
 [11 13 15]]
[[0 0 0]
 [3 3 3]]
[[ 2  4  6]
 [14 16 18]]
[[  4  16  36]
 [112 160 216]]
[[0.5        0.5        0.5       ]	
 [0.28571429 0.3125     0.33333333]] 
[[    16    256   1296]
 [ 38416  65536 104976]]
30
9
1
[[1 0 3]
 [7 8 9]]
[[1 0 3]
 [7 8 9]]
[[1 0 3]
 [7 8 9]]
[[0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]]
[[1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]]
[[0.5        0.5       ]		#np.empty 盗用数据？！
 [0.5        0.28571429]
 [0.3125     0.33333333]]
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
[[0. 1. 0.]		#一层的高对角
 [0. 0. 1.]]
[[1. 0.]		#‘主对角’
 [0. 1.]
 [0. 0.]]
[[3.50797594e-01 1.07634148e-01]	# random 每次输出不同
 [6.63240857e-01 3.28327606e-01]
 [1.85154738e-01 1.63921209e-04]
 [8.29918942e-01 2.10251101e-01]]
[ 2  7 12 17 22 27 32 37 42 47 52 57 62]
[ 2.  7. 12. 17. 22. 27. 32. 37. 42. 47. 52. 57. 62.]