基于NumPy和Matplotlib实现k-means聚类及可视化

k均值算法

  k均值 (k-means) 算法是一种原型聚类算法（亦称“基于原型的聚类” (prototype-based clustering)）。通常情况下，原型聚类算法先对原型进行初始化，然后对原型进行迭代更新求解。k-means算法以k为参数，把n个对象分成k个簇，使簇内具有较高的相似度，而簇间的相似度较低。
  给定样本集$D=\{{\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_m\}$，k均值算法针对聚类所得簇划分$C=\{C_1,C_2,...,C_k\}$最小化平方误差$$E={\Sigma }_{i=1}^k{\Sigma }_{\mathbf{x}\in C_i}||\mathbf{x}-{\mathbf{\mu }}_i|{|}_2^2,$$其中${\mathbf{\mu }}_i=\frac{1}{|C_i|}{\Sigma }_{\mathbf{x}\in C_i}$，$\mathbf{x}$是簇$C_i$的均值向量。上式在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度，$E$值越小则簇内样本相似度越高。
  k均值算法采用了贪心策略，通过迭代优化来近似求解上式。算法流程如下：

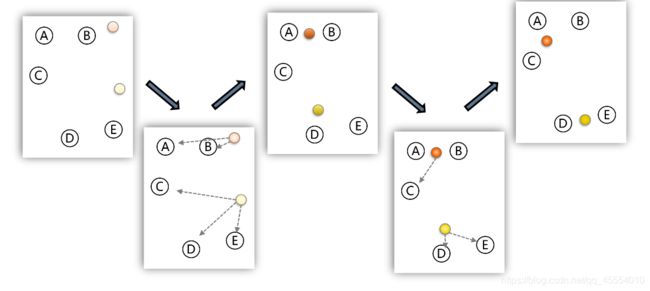
基于NumPy和Matplotlib实现

工作目录结构

dataset.txt

1.658985	4.285136
-3.453687	3.424321
4.838138	-1.151539
-5.379713	-3.362104
0.972564	2.924086
-3.567919	1.531611
0.450614	-3.302219
-3.487105	-1.724432
2.668759	1.594842
-3.156485	3.191137
3.165506	-3.999838
-2.786837	-3.099354
4.208187	2.984927
-2.123337	2.943366
0.704199	-0.479481
-0.392370	-3.963704
2.831667	1.574018
-0.790153	3.343144
2.943496	-3.357075
-3.195883	-2.283926
2.336445	2.875106
-1.786345	2.554248
2.190101	-1.906020
-3.403367	-2.778288
1.778124	3.880832
-1.688346	2.230267
2.592976	-2.054368
-4.007257	-3.207066
2.257734	3.387564
-2.679011	0.785119
0.939512	-4.023563
-3.674424	-2.261084
2.046259	2.735279
-3.189470	1.780269
4.372646	-0.822248
-2.579316	-3.497576
1.889034	5.190400
-0.798747	2.185588
2.836520	-2.658556
-3.837877	-3.253815
2.096701	3.886007
-2.709034	2.923887
3.367037	-3.184789
-2.121479	-4.232586
2.329546	3.179764
-3.284816	3.273099
3.091414	-3.815232
-3.762093	-2.432191
3.542056	2.778832
-1.736822	4.241041
2.127073	-2.983680
-4.323818	-3.938116
3.792121	5.135768
-4.786473	3.358547
2.624081	-3.260715
-4.009299	-2.978115
2.493525	1.963710
-2.513661	2.642162
1.864375	-3.176309
-3.171184	-3.572452
2.894220	2.489128
-2.562539	2.884438
3.491078	-3.947487
-2.565729	-2.012114
3.332948	3.983102
-1.616805	3.573188
2.280615	-2.559444
-2.651229	-3.103198
2.321395	3.154987
-1.685703	2.939697
3.031012	-3.620252
-4.599622	-2.185829
4.196223	1.126677
-2.133863	3.093686
4.668892	-2.562705
-2.793241	-2.149706
2.884105	3.043438
-2.967647	2.848696
4.479332	-1.764772
-4.905566	-2.911070
0.000003	3.000003
0.500001	2.890000
-0.500067	3.752312
-0.678531	2.752312
-1.234562	3.555612
1.234562	3.564231
0.769825	2.895642
0.965432	3.865231
1.456785	2.756213
0.000009	1.123452
0.100231	1.234562
0.352465	0.976532
0.536489	0.865321
1.235465	1.567835
1.345675	1.468792
-2.207066	1.123546
-1.100231	1.678542
1.403367	1.956213
1.345687	1.756142
1.345687	1.756142
0.200003	2.134568
-0.234562	1.023456
4.000235	-2.135432
4.123856	-3.756423
-4.561235	-4.563214
5.461454	-5.123464
4.012356	-4.985623

MyKMeans.py

"""
MyKMeans.py - 基于NumPy实现KMeans聚类算法
K-means算法以k为参数，把n个对象分成k个簇，使簇内具有较高的相似度，而簇间的相似度较低。
处理过程：
    1.随机选择k个点作为初始的聚类中心。
    2.对于剩下的点，根据其与聚类中心的距离，将其归入最近的簇。
    3.对每个簇，计算所有点的均值作为新的聚类中心。
    4.重复步骤2、3直到聚类中心不再发生改变。
"""
import numpy as np


def InitializeCentroids(points, k):
    """
    KMeans聚类算法初始化，随机选择k个点作为初始的聚类中心
    :param points: 样本集
    :param k: 聚类簇数
    :return: 随机选择的k个聚类中心
    """
    centroids = points.copy()
    np.random.shuffle(centroids)
    return centroids[:k]


def ClosestCentroid(points, centroids):
    """
    计算每个样本与聚类中心的欧式距离，将其归入最近的簇
    :param points: 样本集
    :param centroids: 聚类中心
    :return: 样本所属聚类的簇
    """
    euclDist = np.sqrt(((points - centroids[:, np.newaxis]) ** 2).sum(axis=2))
    return np.argmin(euclDist, axis=0)


def UpdateCentroids(points, closestCentroid, centroids):
    """
    对每个簇计算所有点的均值作为新的聚类中心
    :param points: 样本集
    :param closestCentroid:
    :param centroids: 上一轮迭代的聚类中心
    :return: 新的聚类中心
    """
    return np.array([points[closestCentroid == k].mean(axis=0) for k in range(centroids.shape[0])])


def KMeans(points, k=3, maxIters=10):
    """
    KMeans聚类算法实现
    :param points: 样本集
    :param k: 聚类簇数
    :param maxIters: 最大迭代次数
    :return: 聚类后的簇划分
    """
    centroids = InitializeCentroids(points=points, k=k)
    for i in range(maxIters):
        closestCentroid = ClosestCentroid(points=points, centroids=centroids)
        newCentroids = UpdateCentroids(points=points, closestCentroid=closestCentroid, centroids=centroids)
        if (newCentroids == centroids).all():    # 聚类中心不再发生改变，停止迭代
            break
        centroids = newCentroids
    return centroids, closestCentroid, points

KMeansDemo.py

import matplotlib.pyplot as plt
import numpy as np

import MyKMeans


# 加载数据集
data = np.loadtxt('./dataset.txt')
plt.scatter(data[:, :1], data[:, 1:2])
plt.xlabel('x')
plt.ylabel('y')
plt.title('Raw Data')
plt.savefig('./RawData.jpg')
plt.show()

# KMeans聚类
k = 3
centroids, closestCentroid, points = MyKMeans.KMeans(data, k, 10)

# 可视化
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k', 'w']
markers = ['+', 'x', 's', 'p', 'o', '^', 'v', '.']
for i in range(k):
    cluster = []
    clusterCenter = plt.scatter(centroids[i:i + 1, :1], centroids[i:i + 1, 1:], s=150, c=colors[i], marker='*',
                                label='Cluster Center {}'.format(i + 1))
    for j in range(len(closestCentroid)):
        if closestCentroid[j] == i:
            cluster.append(points[j])
    cluster = np.array(cluster)
    plt.scatter(cluster[:, :1], cluster[:, 1:], s=50, c=colors[i], marker=markers[i], label='Cluster {}'.format(i + 1))
plt.legend(loc='best')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Data Clustering by K-Means')
plt.savefig('./DataClusteringByKMeans.jpg')
plt.show()

运行结果