ACM Weekly 2

涉及的知识点

第二周练习主要涉及常见数据类型范围、复杂度估算运行时间、Java的BigInteger、运算相关、几何、记忆化
拓展：setw()，setwill()，大数乘/除(快速傅里叶变化或快速数论变换，后期自行了解)，负进制（后期自行了解），Java的BigDecimal，快读，精度问题

常见数据类型范围

数据类型	范围
char	-128~127（1 Byte，约3位）
short	-32768~32767（2 Byte，约5位）
unsighed short	0~65536（2 Byte，约5位）
int	-2147483648~2147483647（4 Byte，约10位）
unsighed int	0~4294967295（4 Byte，约10位）
long	同int
long long	-9223372036854775808~9223372036854775807（8 Byte 约19位）
unsigned long long	0~18446744073709551615（8 Byte 约20位）
_int64	同long long
unsigned _int64	同 unsigned long long
double	1.7*10^308（8 Bytes）

复杂度估算运行时间

竞赛中一般认为计算机速度为5*10⁸次/s，若题目时间限制1s，则计算次数最多到10⁸才可能完成题目。

• O($n$) 的算法能解决的数据范围在 $n$≤10⁸

• O($nlogn$) 的算法能解决的数据范围在 $n$≤10⁶

• O($n\sqrt{n}$) 的算法能解决的数据范围在 $n$≤10⁵

• O ($n$²) 的算法能解决的数据范围在 $n$ ≤ 5000

• O ($n$³) 的算法能解决的数据范围在$n$≤300

• O(2ⁿ) 的算法能解决的数据范围在$n$≤ 25

• O($n!$) 的算法能解决的数据范围在$n$≤11

Java的BigInteger

C++中无高精度运算，只能手动模拟运算过程，而Java的java.math包中的BigInteger提供高精度运算，该类大小无上限

对象相关
使用BigInteger类，首先引用该包

import java.math.BigInteger;

创建该类对象

BigInteger a=new BigInteger("123456");

修改值

String str = "123456";
BigInteger a = BigInteger.valueOf(str);//此时a为123456
int n = 1;
BigInteger a = BigInteger.valueOf(n);//此时a为1

基本常量如下

a = BigInteger.ONE // 1
b = BigInteger.TEN // 10
c = BigInteger.ZERO // 0

一些使用方法

Scanner in = new Scanner(System.in); 
while(in.hasNext()) //等同于!=EOF
{
     
    BigInteger a;
    a = in.nextBigInteger();//直接读入
    /*String s = in.nextLine();
    BigInteger a = new BigInteger(s);间接读入*/
    System.out.print(a.toString());
}

该类的输出有多重选择

System.out.print(a);//直接输出
System.out.print(a.toString(n));//以n进制字符串输出，n可以不传入，此时默认n=10

BigInteger n = new BigInteger("12");
System.out.println(n.bitLength()); // 4
//输出二进制长度，注意n.bitLength()含义

判断，四则运算，以及特殊运算

大小通过equals()和compareTo()来判断，使用格式如a.equals(b)或者a.compareTo(b);

加减乘除、取余、最大公约数为
add()、subtract()、multiply()、divide()、remainder()、gcd()，用法和判断大小相同

除法取余
BigInteger result[] = b.divideAndRemainder(a); //该方法返回的是数组
System.out.println("商是：" + result[0] + "；余数是：" + result[1]);

绝对值、相反数、幂
abs()、negate()、pow(t)用法形如a.xxx()

运算相关

万进制

以万进制计算，逢万进一，计算时可将每4位数存入数组中的一个单元中作为万进制的一位。

例题1（HDU 1042）

题目大意：计算N的阶乘，范围从0~10000

思路：直接用万进制进行运算

代码

#include 
#include //必备头文件
using namespace std;
int N=0;
int main()
{
     
    while(cin >>N)
    {
     
        int output[12121]= {
     1};
        int digit=0,carry=0;
        for(int i=1; i<=N; i++)
        {
     
            carry=0;
            for(int j=0; j<=digit; j++)
            {
     
                output[j]=output[j]*i+carry;/*和每一位(万进制)相乘*/
                carry=output[j]/10000;//获得进位
                output[j]%=10000;//去掉进位
            }
            if(carry)
                output[++digit]=carry;//如果产生进位，开辟新的位数
        }
        cout <<output[digit];
        for(int i=digit-1; i>=0; i--)
            cout<<setw(4)<<setfill('0')<<output[i];//setw()和setfill()为拓展
        cout <<endl;
    }
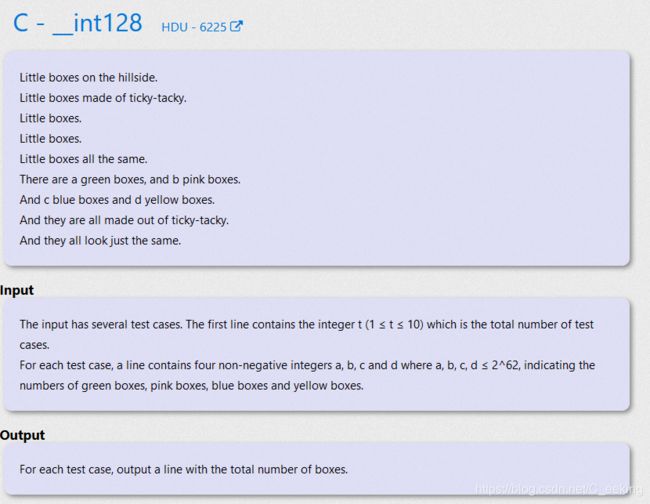
    return 0;
}

例题2（HDU 6225）

题目大意：给出四个数，计算它们的和（每个数的范围可到128位2进制）

思路：用万进制进行计算

代码

#include 
#include 
#include 
#include 
#include 
using namespace std;
int N;
int digit[4];
int main()
{
     
    cin >>N;
    while(N--)
    {
     
        int addend[12121]= {
     0},i=0;
        char input[12121]= {
     '\0'};
        cin >>input;
        for(i=strlen(input)-1; i-3>=0; i-=4)
        {
     
            char tmp[5]= {
     '\0'};
            strncpy(tmp,input+i-3,4);
            addend[digit[0]++]=atoi(tmp);
        }
        if(input[i]!='\0')
        {
     
            char tmp[5]= {
     '\0'};
            strncpy(tmp,input,i+1);
            addend[digit[0]++]=atoi(tmp);
        }
        for(int p=1; p<=3; p++)
        {
     
            int augend[12121]= {
     0};
            char inp[12121]= {
     '\0'};
            cin >>inp;
            for(i=strlen(input)-1; i-3>=0; i-=4)
            {
     
                char tmp[5]= {
     '\0'};
                strncpy(tmp,inp+i-3,4);
                augend[digit[p]++]=atoi(tmp);
            }
            if(input[i]!='\0')
            {
     
                char tmp[5]= {
     '\0'};
                strncpy(tmp,inp,i+1);
                augend[digit[p]++]=atoi(tmp);
            }
            for(int k=0,j=0; k<=max(digit[0],digit[i])&&j<=max(digit[0],digit[i]); k++,j++)
            {
     
                int carry=0;
                addend[k]+=augend[j];
                carry=addend[k]/10000;
                addend[k]%=10000;
                if(carry)
                {
     
                    addend[k+1]+=carry;
                    if(k+1>digit[0]-1)
                        digit[0]++;
                }
            }
        }
        cout <<addend[--digit[0]];
        for(i=digit[0]-1;i>=0;i--)
            cout <<setw(4)<<setfill('0')<<addend[i];
        cout <<endl;
        memset(digit,0,sizeof(digit));
    }
    return 0;
}

例题3（HDU 1002）

题目大意：计算两个大数（正整数）的和

思路：万进制模拟

#include 
#include 
#include 
#include 
#include 
using namespace std;
int main()
{
     
    int T;
    cin >>T;
    for(int n=1;n<=T;n++)
    {
     
        int A[1212]= {
     0},B[1212]= {
     0},a=0,b=0,i=0;//从左到右：A,B，A的位数，B的位数
        char input[1212]= {
     '\0'};
        cin >>input;
        cout <<"Case "<<n<<":"<<endl;
        cout <<input<<" "<<"+ ";
        for(i=strlen(input)-1; i-3>=0; i-=4)//每取4位进行一次转换
        {
     
            char tmp[5]= {
     '\0'};
            strncpy(tmp,input+i-3,4);
            A[a++]=atoi(tmp);
        }
        if(input[i]!='\0')
        {
     
            char tmp[5]= {
     '\0'};
            strncpy(tmp,input,i+1);
            A[a++]=atoi(tmp);
        }
        cin >>input;
        cout <<input<<" "<<"= ";
        for(i=strlen(input)-1; i-3>=0; i-=4)
        {
     
            char tmp[5]= {
     '\0'};
            strncpy(tmp,input+i-3,4);
            B[b++]=atoi(tmp);
        }
        if(input[i]!='\0')
        {
     
            char tmp[5]= {
     '\0'};
            strncpy(tmp,input,i+1);
            B[b++]=atoi(tmp);
        }
        for(int k=0,j=0; k<=max(a,b)&&j<=max(a,b); k++,j++)//每位相加
        {
     
            int carry=0;
            A[k]+=B[j];
            carry=A[k]/10000;
            A[k]%=10000;
            if(carry)
            {
     
                A[k+1]+=carry;
                if(k+1>a-1)
                    a++;
            }
        }
        a=max(a,b);
        cout <<A[--a];
        for(i=a-1; i>=0; i--)
            cout <<setw(4)<<setfill('0')<<A[i];
        cout <<endl;
        if(n!=T)
            cout <<endl;
    }
    return 0;
}

字符串模拟进位

将输入的数字转换成字符串进行存储，并进行模拟进位。

例题1（HDU 2100）

题目大意：略

思路：字符串模拟

代码

#include 
#include 
#include 
#include 
#include 
using namespace std;
char a[300],b[300],c[300];
int main()
{
     
    //freopen("test.txt","r",stdin);
    while(scanf("%s",a)!=EOF&&scanf("%s",b)!=EOF)
    {
     
        int tmp=0,carry=0,i=0,j=0,k=0;
        reverse(a,a+strlen(a));
        reverse(b,b+strlen(b));//翻转，便于后面操作
        if(strlen(a)>strlen(b))//对齐
            for(i=strlen(b); i<strlen(a); i++)
                b[i]='A';
        else if(strlen(a)<strlen(b))
            for(i=strlen(a); i<strlen(b); i++)
                a[i]='A';
        for(i=0,j=0,k=0; i<strlen(a)&&j<strlen(b); i++,j++,k++)
        {
     
            tmp=carry+a[i]-'A'+b[j]-'A';
            carry=tmp/26;
            tmp%=26;
            c[k]=tmp+'A';
        }
        c[k]=carry+'A';
        while(c[k]=='A')k--;//去掉高0位
        for(i=k; i>=0; i--)
            cout <<c[i];
        if(k==-1)
            cout <<'A';
        cout <<endl;
        memset(a,'\0',sizeof(a));//清空
        memset(b,'\0',sizeof(b));
        memset(c,'\0',sizeof(c));
    }
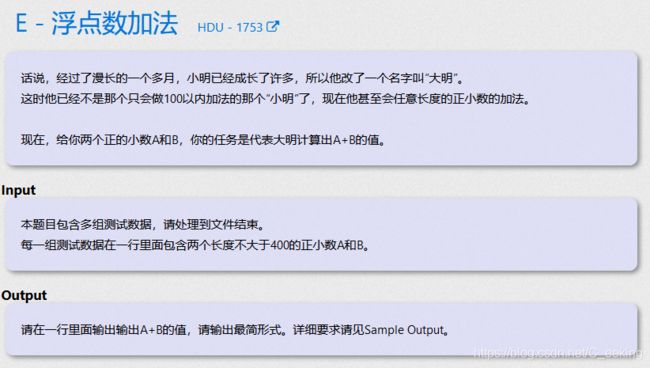
    return 0;
}

例题2（HDU 1753）

题目大意：略

思路：字符串模拟运算，注意小数点的位置

代码

#include 
#include 
#include 
#include 
char a[1010],b[1010];
int A[1010],B[1010],acc[1010];
using namespace std;
int main()
{
     
    while(~scanf("%s %s",a,b))
    {
     
        memset(A,0,sizeof(A));
        memset(B,0,sizeof(B));
        memset(acc,0,sizeof(acc));
        int point_a=strlen(a),point_b=strlen(b);
        for(int i=0; i<strlen(a); i++)//找小数点，strlen()应当修改，因为每一次调用都会重新算
            if(a[i]=='.')
            {
     
                point_a=i;
                break;
            }
        for(int i=0; i<strlen(b); i++)
            if(b[i]=='.')
            {
     
                point_b=i;
                break;
            }
        for(int i=point_a+1,j=499; i<strlen(a); i++,j--) //将两个数逆序并去掉小数点存到数组中(重要)
            A[j]=a[i]-'0';
        for(int i=point_a-1,j=500; i>=0; i--,j++)
            A[j]=a[i]-'0';
        for(int i=point_b+1,j=499; i<strlen(b); i++,j--)
            B[j]=b[i]-'0';
        for(int i=point_b-1,j=500; i>=0; i--,j++)
            B[j]=b[i]-'0';
        int carry=0;
        for(int i=0; i<1000; i++)
        {
     
            acc[i]=A[i]+B[i]+carry;
            carry=acc[i]/10;
            acc[i]%=10;
        }
        int i=999;
        while(acc[i]==0&&i>500)//去除前导零
            i--;
        for(int j=i; j>=500; j--)
            printf("%d",acc[j]);
        i=0;
        while(acc[i]==0&&i<500)//去除后导零
            i++;
        if(i!=500)//判断是否输出小数点(思考为什么)
        {
     
            printf(".");
            for(int j=499; j>=i; j--)
                printf("%d",acc[j]);
        }
        printf("\n");
    }
    return 0;
}
//该方法通过空间上的设置完成了对位

_int128

_int128和Java中的大数类有相似之处，但是需要自己构造输入和输出函数，并且有的编译器不接受它的存在。

例子
_int128的输入函数

代码

//和字符串模拟差不多
inline __int128 read() {
     
	__int128 data=0,t=1;
	char ch=getchar();
	while(ch<'0'||ch>'9') 
	{
     
		if(ch=='-')t=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
     
		data=data*10+ch-'0';
		ch=getchar();
	}
	return data*t;
}

例子
_int128的输出函数

inline void write(__int128 data) {
     
	if(data<0) {
     
		cout <<"-";
		//putchar('-');
		data=-data;
	}
	if(data>9)write(data/10);
	cout <<data%10+'0';
	//putchar(data%10+'0');
}

几何

重要结论

$|\overrightarrow{a}\times \overrightarrow{b}|=x_a\times y_b-x_b\times y_a$ （叉乘性质）

例题1（POJ 1269）

题目大意：输入四个点坐标，判断对应组成的直线间关系，若相交则输出相交点坐标

思路：通过几何中向量之间的关系来进行判断，将给出的点对应化成向量，向量叉乘为0代表$\sin <a,b>$为0，至少平行，如果一条边的两点相对于另一条边的同一点构成的向量平行，则代表重合，其余情况为相交，求出交点即可，证明过程详细如图

代码

#include 
#include 
#include 
#include 
#define eps 1e-8
using namespace std;
int n=0;
int judge(double x)//设定判断，因为double类型不能直接比较，且因为精度问题，所以需要手动设置
{
     
    if(fabs(x)<eps)
        return 0;
    if(x<0)
        return -1;
    return 1;
}//判断叉乘结果
typedef struct Point
{
     
    double x,y;
    Point(){
     }
    Point(double _x,double _y)
    {
     
        x=_x;
        y=_y;
    }
    Point operator-(const Point&p)const//重载"-"号，相当于返回一个向量
    {
     
        return Point(x-p.x,y-p.y);
    }
    double operator*(const Point&p)const//重载"*"，相当于"·"乘
    {
     
        return x*p.x+y+p.y;
    }
    double operator^(const Point&p)const//重载"^"，相当于"×"乘
    {
     
        return x*p.y-y*p.x;
    }
} Point;
typedef struct Line
{
     
    Point a,b;
    Line(Point _a,Point _b)
    {
     
        a=_a;
        b=_b;
    }
    pair<Point,int>operator&(const Line&p)
    {
     
        Point tmp=a;
        if(judge((a-b)^(p.a-p.b))==0)//如果向量l1和向量l2叉乘为0，则至少平行
        {
     
            if(judge((p.a-a)^(p.b-a))==0)//如果向量l1的两点与l2的某一点形成的两个向量平行，则说明相交
                return make_pair(tmp,0);//平行+相交=重合
            return make_pair(tmp,1);
        }
        double t=((a-p.a)^(p.a-p.b))/((a-b)^(p.a-p.b));//具体参考图与证明过程
        tmp.x+=(b.x-a.x)*t;
        tmp.y+=(b.y-a.y)*t;
        return make_pair(tmp,2);
    }
}Line;
int main()
{
     
    cout << "INTERSECTING LINES OUTPUT" << endl;
    cin >>n;
    while(n--)
    {
     
        double x1,x2,x3,x4,y1,y2,y3,y4;
        cin >>x1>>y1>>x2>>y2>>x3>>y3>>x4>>y4;
        Line l1(Point(x1,y1),Point(x2,y2));
        Line l2(Point(x3,y3),Point(x4,y4));
        pair<Point,int> tmp=l1&l2;
        if(tmp.second==2)
            printf("POINT %.2f %.2f",tmp.first.x,tmp.first.y);
        else if(tmp.second==1)
            cout <<"NONE";
        else
            cout <<"LINE";
        cout <<endl;
    }
    cout <<"END OF OUTPUT";
    return 0;
}

关于相交情况下求点坐标的证明

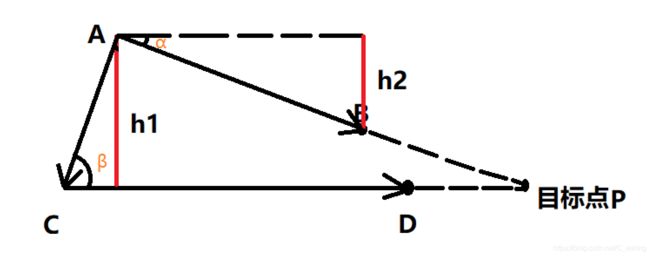
由代码，证明t为垂线段h1、点A、P构成的三角形和垂线段h2、点B、A构成的三角形的相似比。
证明如下：
$t=\frac{|\overrightarrow{\mathrm{AC}}||\overrightarrow{\mathrm{CD}}|\sin (\pi -\beta )}{|\overrightarrow{\mathrm{CD}}||\overrightarrow{\mathrm{AB}}|\sin \alpha }$
CD被约分，剩下的分子分母的值分别为h1、h2高度，得出t为两三角形相似比。
因此，P点横坐标为A点坐标加上AB间横坐标差值乘以相似比，P点纵坐标同理。

记忆化

通过记录先前已经使用过的数据，减小时间复杂度，例如斐波那契数列的求项，通过记录已经算过的项数来减少重复。

代码

typedef long long ll;
ll a[1000000];
ll fib(int x)
{
     
	if(a[x])
		return a[x];
	return a[x]=fib(x-1)+fib(x-2);
}

unordered_map
unordered_map为关联容器，利用哈希表来进行检索、插入、删除。

API文档

由API文档可得知，构造函数只需要<键，值>其余可使用缺省值，使用时和map类似，各个函数的具体用法参考API文档中的详说明。

难题解析

CodeForces 10451

题目大意：输入N个字符串，判断有多少对字符串可以组合成回文串（不包括自己）。

思路：在写入的时候无需存入每个字符串的全部内容，只需记录各个字母数量的奇偶，偶数直接削减到0，奇数则置1，于是可以使用二进制代码的思维来存储字母个数的奇偶，在二进制的原理使用不熟悉的情况下，可以通过十进制（变相二进制数）来判断。对于本题，能够成立的情况只有全为偶数，或者只有一个奇数其余全为偶数的情况，所以只需判断这两种情况。

代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define int long long
#define INF 0x3f3f3f3f
using namespace std;
const int maxn = 1e6 + 7;
char ch[maxn];
int num[26], _num[26];
void Init(){
     
    num[0] = 1;
    for (int i=1; i<26; i++) num[i] = num[i-1] * 2;
}//初始化，每一位存字母所对应的二进制数的十进制数
signed main(){
     
    Init();
    int n; scanf("%lld", &n);
    unordered_map <int, int> m;//使用类似数组，记录字符串数量
    unordered_map <int, int> _m;//记录去掉一个奇数字母后的串所对应的数量
    int p = 0;
    for (int i=1; i<=n; i++){
     
        memset(_num, 0, sizeof (_num));
        scanf("%s", ch);
        int ln = (int) strlen(ch);
        for (int j=0; j<ln; j++){
     //去掉偶数
            _num[ch[j] - 'a'] ++;
            while (_num[ch[j] - 'a'] >= 2) _num[ch[j] - 'a'] -= 2;
        }
        int ans = 0;
        for (int j=0; j<26; j++){
     
            if (_num[j] > 0) {
     
                ans += num[j];//记录有哪些字母
            }
        }
        for (int j=0; j<26; j++){
     
            if (_num[j]){
     
                _m[ans - num[j]] ++;//记录字符串去掉一个(即在合成的时候设定改字母为奇数个)，剩下的作为合成后变成偶数个
            }
        }    
//        printf("ans: %lld\n", ans);
        m[ans] ++;//记录字符串数量，不同的ans值对应的字符串情况是唯一的
    }
    int res = 0;
    for (auto i:m){
     
        res += i.second * _m[i.first];
        //该式表示，对于A串，如果其余串中有去掉一个为奇的字母后和它相同的串，则加上A串个数和去掉一个字母后与A串相等的个数的乘积
        res += (i.second - 1) * i.second / 2;//该式表示，对于m中的一种串，将该种串的所有元素排列组合，并记录不重复的个数
//        printf("%lld %lld\n", i.first, i.second);
    }
    printf("%lld\n", res);
    return 0;
}

拓展的知识点

setw(int t)
设置字符的宽度，固定值
setfill(char c)
设置用什么字符填充

以上两者合用效果类似于printf("%cnd")，c、n定义相同

快读
在C++中getchar()的速度是高于cin、scanf的，为了加快读取的速度，通过getchar()循环来提高读取速度，但代码的运算速度主要还是靠算法。

以下为几种快读的代码

inline void read(int &x)
{
     
    int data=0,type =1;
    char ch=getchar();//判断符号
    while(ch<'0'||ch>'9')
    {
     
        if(ch=='-') type =-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')//记录数值
    {
     
        data=data*10+ch-'0';
        ch = getchar();
    }
    x = data*type;
}

template <class T>//使用模板
inline void (T &x)
{
     
    T type=1,ch=getchar();
    x=0;
    while(!isdigit(ch))//判断是否为数字
    {
     
        if(ch=='-')w=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
     
        x=x*10+ch-'0';
        ch=getchar();
    }
    x*=type;
}

//字符串快读
inline string read()
{
     
    char ch = getchar();
    string str="";
    while(!(ch>='a'&&ch<='z'))ch=getchar();
    while(ch>='a'&&ch<='z')
    {
     
        str+=ch;
        ch = getchar();
    }
    return str;
}

//快写
inline void write(int x)
{
     
    if(x<0)
    {
     
        putchar('-');
        x=-x;
    }
    if(x>9)
        write(x/10);
    putchar(x%10+'0');
}

精度问题
float最大值：3.4e38
float精度：1.19e-7
double最大值：1.79e308
double精度：2.22e-16

Java的BigDecimal
BIgDecimal类的基本操作与BigInteger类似，只记录不同点。

导入

import java.math.BigDecimal;

输出相关

BigDecimal a = new BigDecimal("100000.0000");
System.out.println( a.stripTrailingZeros().toString());
//输出为科学计数法1E+5
a.stripTrailingZeros().toPlainString());
//输出为100000
//如果格式化输出需要引入包import java.math.RoundingMode;
 BigDecimal  b =a.setScale(2, RoundingMode.HALF_UP);//保留两位小数
System.out.println(b);
//输出为100000.00

小拓展
关于setScale()
setScale(1)：默认小数点后一位，四舍五入
setScale(1)表示保留一位小数，默认四舍五入

setScale(1,BigDecimal.ROUND_DOWN)删除多余的小数位，如3.35会变成3.3 ，注意ROUND_DOWN

setScale(1,BigDecimal.ROUND_UP)进位处理，3.35变成3.4 ，注意ROUND_UP

setScale(1,BigDecimal.ROUND_HALF_UP)直接四舍五入末尾，注意ROUND_HALF_UP

setScaler(1,BigDecimal.ROUND_HALF_DOWN)四舍五入，如果是5则向下舍，注意ROUND_HALF_DOWN，与ROUND_HALF_UP不同

setScaler(1,BigDecimal.ROUND_CEILING)接近正无穷大的舍入

setScaler(1,BigDecimal.ROUND_FLOOR)接近负无穷大的舍入，当数字为正，作用同ROUND_UP，为负同ROUND_DOWN

setScaler(1,BigDecimal.ROUND_HALF_EVEN)向最接近的数字舍入，如果与两个相邻数字的距离相等，则向相邻的偶数舍入。