ACM Weekly 7(待修改)
ACM Weekly 7
- 涉及的知识点
-
- DFS
- BFS
- 记忆化搜索
- 难题解析
- 拓展
-
- 深搜剪枝
- 参考文献
涉及的知识点
第六周的练习主要涉及深度优先搜索DFS、广度优先搜索BFS、记忆化搜索
拓展:深搜剪枝、SPFA、基环树、负环判断、差分约束
DFS
深度优先搜索,是常用的状态遍历的方法,通俗来讲,其核心思想便是一条路走到头,遍历所有状态,求出所有可行解
代码实现
void DFS(int& i)
{
if(i>=N)//到达边界就返回
return ;
for(int j=1;j<=N;j++)
if(!visited[j])
{
visited[j]=true;//在DFS前可以增加操作
DFS(j);
visited[j]=false;//还原使用,有时也不需要
}
}
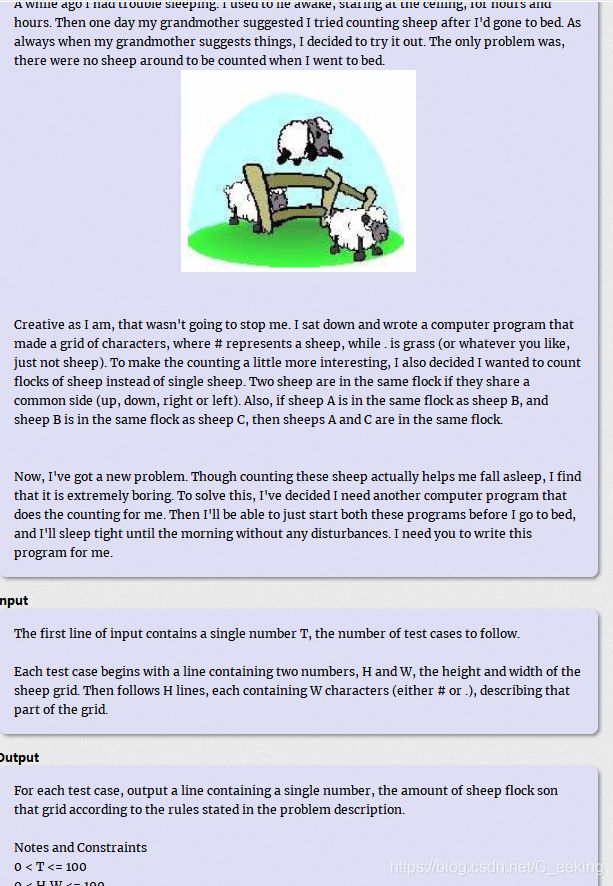
例题
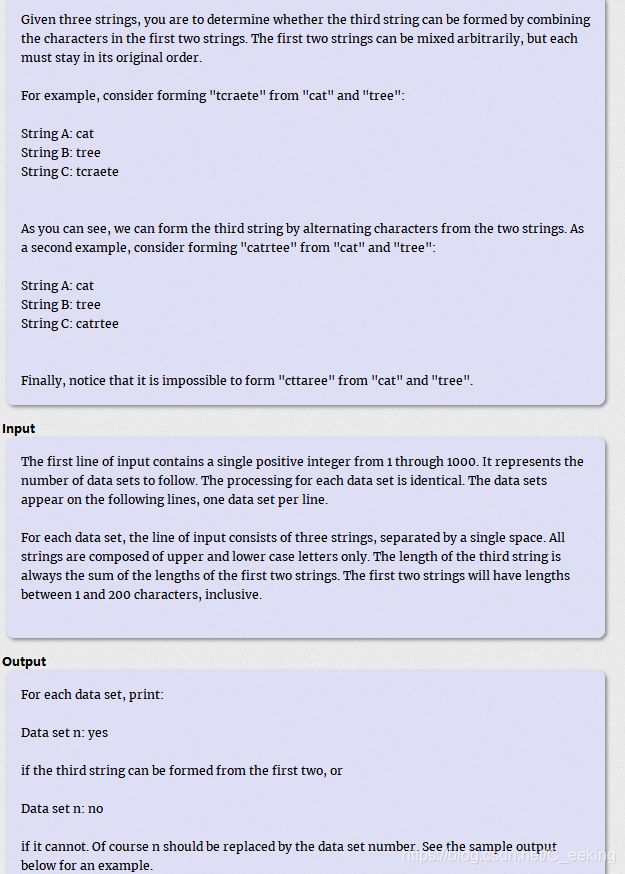
题目大意:给出三个字符串A、B、C,判断A与B在不变更相对顺序的情况下能否合成C
思路:直接DFS,从A、B中抽取和C对应位置字符相等的元素进行判断,A不行再判断B,B不行说明不能合成
代码
#include BFS
广度优先搜索BFS,与DFS重要性平分秋色,通俗讲便是层次遍历,将首个点点周边所有点进行拓展,作为一层,删除该点,以此类推,求出最优解
代码实现
typedef pair<int,int>PR;
int Next[4][2]={
0,1,0,-1,1,0,-1,0};
void BFS(PR root)
{
queue<PR>Q;
Q.push(root);
while(!Q.empty())
{
PR t=Q.front();
Q.pop();
if(visited[t.first][t.second])
continue;
visited[t.first][t.second]=true;
for(int i=0;i<4;i++)
{
int x=t.first,y=t.second;
x+=Next[i][0];
y+=Next[i][1];
if(x>=1&&x<=N&&y>=1&&y<=M&&!visited[x][y]&&!Graph[x][y])
Q.push(make_pair(x,y));
}
}
}
例题
思路:直接BFS,数据规模小,并且到了后面还会越来越快,可以直接暴力
代码
#include 记忆化搜索
记忆化搜索即搜索+记录上一层已经计算的结果,思想是搜索+动态规划,记录已经算出的结果,可以省略大量重复的步骤,从而提高效率
由于记忆化搜索总结出通用性代码不太现实,所以直接采用例题分析
例题1
思路:直接模拟+记录已算出数值,由给出的递归思路可知,可以先预处理w(20,20,20)
代码
#include 例题2
思路:
代码
难题解析
例题1
拓展
深搜剪枝
- 最优化剪枝
- 估价函数剪枝
- 双向搜索
- 较优解
- 阈值剪枝
- 随机(搜索数据或顺序)
当搜索答案的变化方向远离正确答案时,去掉之后的未搜索的状态
参考文献
- 《啊哈算法》
- 《挑战程序设计竞赛》