目标检测(三)——IoU总结与代码实现（可完整实现）

IoU基本含义

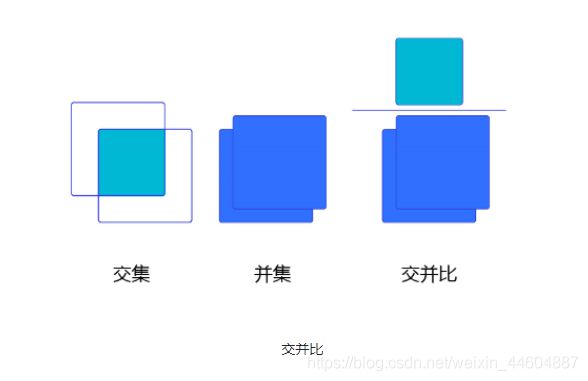
IoU: 简单来说，就是锚框与真实框的交集与锚框与真实框的并集之比。
$$IoU=\frac{A\cap B}{A\cup B}$$
其中：

• A 是真实框
• B 是预测框——也就是锚框

形象的表示为:

如何确定A,B之间的交集呢？

首先，假设A，B的bbox数据：
$$\begin{gathered} A=[x_{a1},y_{a1},x_{a2},y_{a2}] \\ B=[x_{b1},y_{b1},x_{b2},y_{b2}] \end{gathered}$$
而此时的交集情况:

因此，交集的左上角坐标就是A,B的左上角x，y的最大值:【以x向右为正，y向下为正，均从0开始】
$$\begin{gathered} inte{r}_{x1}=max(x_{a1},x_{b1}) \\ inte{r}_{y1}=max(y_{a1},y_{b1}) \end{gathered}$$
而右下角的顶点则是A,B的右下角最小值：
$$\begin{gathered} inte{r}_{x2}=min(x_{a2},x_{b2}) \\ inte{r}_{y2}=min(y_{a2},y_{a2}) \end{gathered}$$
此时，交集的长宽就可以得到了:【长度由具体的像素个数决定，因此需要加1】
$$\begin{gathered} inte{r}_w=max(inte{r}_{x2}-inte{r}_{x1}+1.0,0.) \\ inte{r}_h=max(inte{r}_{y2}-inte{r}_{y1}+1.0,0.) \end{gathered}$$
因此，交集面积:
$$S_{inter}=inte{r}_w\ast inte{r}_h$$
最后我们计算一下并集的面积:

A, B框的面积：
$$\begin{gathered} S_A=(x_{a2}-x_{a1}+1.0)\ast (y_{a2}-y_{a1}+1.0) \\ {S}_B=(x_{b2}-x_{b1}+1.0)\ast (y_{b2}-y_{b1}+1.0) \end{gathered}$$
并集面积:
$$unio{n}_{a}rea=S_A+S_B-S_{inter}$$
此时的交并集IoU：
$$IoU=\frac{S_{inter}}{unio{n}_{a}rea}=\frac{S_{inter}}{S_A+S_B-S_{inter}}$$

示例：【黄色区域就是交集面积】

下面，我们通过代码来进行IoU计算和交集可视化绘制！

代码实践

0. 导入的基本库

import numpy as np  # 可能用到的数据值计算库
import os           # 可能用到的文件操作
import matplotlib.pyplot as plt   		# 图形绘制 
import matplotlib.patches as patches 	# 添加矩形框
import matplotlib.image as image  		# 读取图像数据

1. Bounding box 表示

这里涉及使用bounding box的绘制来可视化交集，所以构建一个bounding box的数据格式函数——因为bounding box具有两种不同的数据表示，两种表示在最终计算上，步骤有所不同。

def BoundingBox_Denote(bbox=[], mode=True):
    '''边界框的表示形式的转换
        bbox: 包含(x1, y1, x2, y2)四个位置信息的数据格式
        mode: 边界框数据表示的模式
             True:  to (x1,y1,x2,y2)
             False: to (x,y,w,h)
        
        return: 返回形式转换后的边界框数据
    '''
    denote_bbox = [] # 转换表示的边界框

    if mode is True:  # 保持原形式
        denote_bbox = bbox
    else:  # 转换为(center_x, center_y, w, h)
        center_x = (bbox[0]+bbox[2]) / 2.0
        center_y = (bbox[1]+bbox[3]) / 2.0
        w = bbox[2] - bbox[0]
        h = bbox[3] - bbox[1]
        denote_bbox = [center_x, center_y, w, h]
    
    # 返回表示转换的边界框表示
    denote_bbox = np.asarray(denote_bbox,  dtype='float32')
    return denote_bbox

2. 边界框矩形的绘制

这个部分用于边界框的绘制，展示交集的可视化

def draw_rectangle(bbox=[], mode=True, color='k', fill=False):
    '''绘制矩形框
        bbox：边界框数据（默认框数据不超过图片边界）
        mode: 边界框数据表示的模式
             True:  to (x1,y1,x2,y2)
             False: to (x,y,w,h)
        color: 边框颜色
        fill: 是否填充
    '''
    if mode is True: # to (x1,y1,x2,y2)
        x = bbox[0]
        y = bbox[1]
        w = bbox[2] - bbox[0] + 1  # 考虑到实际长度由像素个数决定，因此加1（可按坐标轴上两点间的点数推导）
        h = bbox[3] - bbox[1] + 1
    else: # to (x,y,w,h)
    	# 默认绘制的框不超出边界
        x = bbox[0] - bbox[2] / 2.0
        y = bbox[1] - bbox[3] / 2.0
        w = bbox[2]
        h = bbox[3]
    
    # 绘制边界框
    # patches.Rectangle需要传入左上角坐标、矩形区域的宽度、高度等参数
    # 获取绘制好的图形的返回句柄——用于添加到当前的图像窗口中
    rect = patches.Rectangle((x, y), w, h, 
                             linewidth=1,        # 线条宽度
                             edgecolor=color,    # 线条颜色
                             facecolor='y',      # 
                             fill=fill, linestyle='-')
    
    return rect

3. 为xywh格式的bbox数据提供坐标变换

def bbox_2leftup_2rightdown(bbox):
    '''计算bbox的左上右下顶点
        bbox：框数据——xywh
    '''
    x1 = bbox[0] - bbox[2] / 2.0
    y1 = bbox[1] - bbox[3] / 2.0
    x2 = bbox[0] + bbox[2] / 2.0
    y2 = bbox[1] + bbox[3] / 2.0
    
    return x1, y1, x2, y2

4. IoU计算

这里完成IoU的计算，同时返回IoU计算过程中转换好数据格式的原始边界框与实际的交集区域bbox。

def box_iou_solve(bbox1, bbox2, mode=True):
    '''计算两个框之间的IoU值
        bbox1: 框数据
        bbox2: 框数据
        mode: 框数据表示形式
              True: xyxy
              False: xywh

        IoU的intersection的左上右下顶点: 左上点为

        return IoU, (r_bbox1, r_bbox2, inter_bbox)
             PS：
                IoU： 交并比值
                r_bbox1：转换为xyxy形式的bbox1
                r_bbox2：转换为xyxy形式的r_bbox2
                inter_bbox: 形式为xyxy的交集位置
    '''
    if mode is True:  # bbox数据格式: xyxy
        # 左上右下顶点坐标
        b1_x1, b1_y1, b1_x2, b1_y2 = bbox1[0], bbox1[1], bbox1[2], bbox1[3]
        b2_x1, b2_y1, b2_x2, b2_y2 = bbox2[0], bbox2[1], bbox2[2], bbox2[3]
        # 框的长宽:长度由具体的像素个数决定，因此需要加1
        b1_w, b1_h = bbox1[2] - bbox1[0] + 1.0, bbox1[3] - bbox1[1] + 1.0
        b2_w, b2_h = bbox2[2] - bbox2[0] + 1.0, bbox1[3] - bbox1[1] + 1.0
    else:  # bbox数据格式: xywh
        # 左上右下顶点坐标
        b1_x1, b1_y1, b1_x2, b1_y2 = bbox_2leftup_2rightdown(bbox1)
        b2_x1, b2_y1, b2_x2, b2_y2 = bbox_2leftup_2rightdown(bbox2)
        # 框的长宽
        b1_w, b1_h = bbox1[2], bbox1[3]
        b2_w, b2_h = bbox2[2], bbox2[3]

    # 各自的面积
    s1 = b1_w * b1_h
    s2 = b2_w * b2_h

    # 交集面积
    # 如果考虑多个框进行计算交集——那么应该使用np.maximum——进行逐位比较
    inter_x1 = max(b1_x1, b2_x1)  # 交集区域的左上角
    inter_y1 = max(b1_y1, b2_y1)
    inter_x2 = min(b1_x2, b2_x2)  # 交集区域的右下角
    inter_y2 = min(b1_y2, b2_y2)

    # 长度由具体的像素个数决定，因此需要加1
    inter_w = max(inter_x2 - inter_x1 + 1.0, 0)
    inter_h = max(inter_y2 - inter_y1 + 1.0, 0)
    intersection = inter_w * inter_h

    # 并集面积
    union_area = s1 + s2 - intersection

    # 计算IoU交并集
    IoU = intersection / union_area

    # 整合坐标信息——用于展示交集可视化
    # 返回数据均以xyxy表示
    r_bbox1 = b1_x1, b1_y1, b1_x2, b1_y2
    r_bbox2 = b2_x1, b2_y1, b2_x2, b2_y2
    inter_bbox = inter_x1, inter_y1, inter_x2, inter_y2

    return IoU, (r_bbox1, r_bbox2, inter_bbox)

5. 演示代码

fig = plt.figure(figsize=(12, 8))
ax = plt.gca()

# 图片路径
img_path = os.path.join(os.getcwd(), 'img', '1.jpg')
img = image.imread(img_path) # 读取图片数据
plt.imshow(img)  # 展示图片

bbox1 = [240, 70, 380, 240] 
bbox2 = [300, 100, 440, 300]
denote_mode = True  # 数据格式模式
denote_bbox1 = BoundingBox_Denote(bbox=bbox1, mode=denote_mode)  # 形式转换
denote_bbox2 = BoundingBox_Denote(bbox=bbox2, mode=denote_mode)
iou, bboxs = box_iou_solve(bbox1, bbox2, mode=denote_mode)  # 计算IoU交并比

# 取出IoU转换解析后的bbox数据
r_bbox1 = bboxs[0]   
r_bbox2 = bboxs[1]
inter_bbox = bboxs[2]

# 利用数据进行绘制矩形框
# mode=True: bbox数据应该输入_xyxy
rect1 = draw_rectangle(r_bbox1, mode=True, color='b')
rect2 = draw_rectangle(r_bbox2, mode=True, color='b')
rect3 = draw_rectangle(inter_bbox, mode=True, color='y', fill=True)

ax.add_patch(rect1)  # 将绘制的矩形添加到图片上
ax.add_patch(rect2)
ax.add_patch(rect3)

plt.show()

结果图片

相关链接(持续更新)
目标检测(一)——边界框总结与代码实现（可完整实现）
目标检测(二)——锚框总结与代码实现（可完整实现）