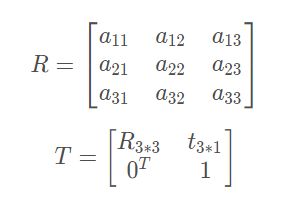视觉SLAM十四讲笔记（超级通俗易懂哦~）

前言

终于来到了心心念念的SLAM学习环节，相信看到这篇文章的你也和我一样按耐不住心中的紧张与激动，那就一起开始卷吧！
在本篇我将简单概述SLAM14讲各个环节的最基本的知识，主要是帮你看看14讲都讲了啥。
想要进一步学习还是看书吧！
Let’s 冲冲冲！

第一讲 预备知识

SLAM：Simultaneous Localization and Mapping
中文名：同时定位与地图构建
基本定义：搭载特定传感器的主体，在没有环境先验信息的情况下，于运动过程中建立环境的模型，同时估计自己的运动。
这里的传感器主要为相机，则为“视觉SLAM”

章节划分

整书分为两大部分：

• 视觉基础篇 1-6讲
• 实践应用篇 7-14讲

第1讲：预备知识
第2讲：SLAM系统概述，介绍SLAM组成模块，各模块具体工作。编程环境搭建以及IDE使用
第3讲：三维刚体运动，主要了解旋转矩阵，欧拉角，四元数，练习使用Eigon
第4讲：学习李群和李代数，定义及使用方式；练习使用Sophus操作
第5讲：针孔相机模型，图像在计算机中的表达；用OpenCV调用相机内外参
第6讲：非线性优化，包括状态估计理论基础，最小二乘问题，梯度下降法；使用Ceres和g2o进行曲线拟合实验
第7讲：基于特征点法视觉里程计，特征提取与匹配，对极几何约束的计算、PnP和ICP等。利用以上方法估计两个图像之间的运动。
第8讲：直接法视觉里程计，学习光流法和直接法原理，利用以上方法实现简单的直接法运动估计。
第9讲：后端优化，主要对Bundle Adjustment（BA）深入讨论，利用稀疏性加速求解过程，利用Ceres和g2o分别书写BA程序。
第10讲：后端优化中的位姿图，介绍SE(3)，Sim(3)位姿图，使用g2o对一个位姿球进行优化
第11讲：回环检测，介绍以词袋模型为主的回环检测，使用DBoW3书写字典训练程序和回环检测程序
第12讲：地图构建，使用单目进行稠密深度图的估计，讨论RGB-D的稠密地图构建过程
第13讲：工程实践，搭建双目视觉里程计框架，综合运用之前的知识，利用Kitti数据集测试性能
第14讲：介绍当前开源SLAM方案以及未来的发展方向

需要具备的基础知识

• 高等数学、线性代数、概率论
• C++语言基础
• Linux系统基础

第二讲 初识SLAM

SLAM回答了两个关键问题：

1. 我在什么地方？——定位
2. 周围环境怎么样？——建图

传感器 Sensors

两类传感器：
安装于环境中的：二维码，GPS，
携带于机器人本体的：
对比激光和相机两大类传感器，激光建图基本上已经研究清楚，视觉SLAM还没有稳定可靠运行
摄像头：轻便、便宜、信息丰富
缺点：遮挡、受光照影响、计算量大、
单目，双目，深度相机（TOF/结构光）

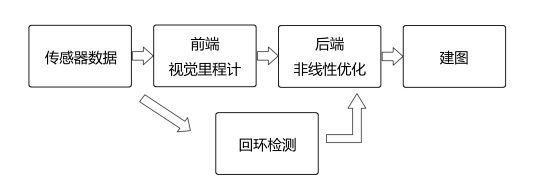
经典视觉SLAM框架

• 传感器信息读取：在视觉SLAM中主要为相机图像信息的读取和预处理。如果是机器人中，还可能是码盘、惯性传感器等信息的读取和同步
• 前端视觉里程计（Visual Odometry，VO）：视觉里程计的任务是估算相邻图像间相机的运动，以及局部地图的样子，又称为前端（Front End）
• 后端非线性优化（Optimization）：后端接受不同时刻视觉里程计测量的相机位姿，以及回环检测的信息，对他们进行优化，得到全局一致的地图。由于在VO之后，又被称为后端（Back End）
• 回环检测（Loop Closure Detection）：回环检测机器人是否到达过先前的位置，如果检测到回环，它会把信息提供给后端进行处理。
• 建图（mapping）：它根据估计的轨迹，建立与任务要求对应的地图

SLAM问题的数学表述

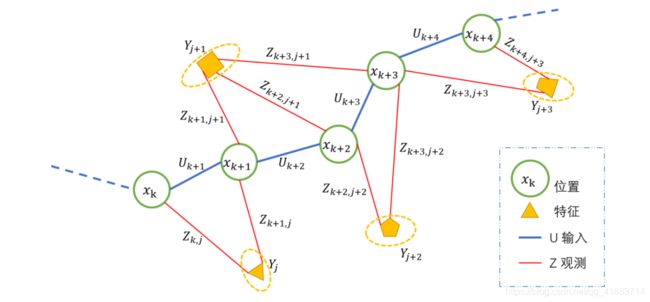
关于SLAM的数学描述，主要有两个方程，分别为位置方程和观测方程：

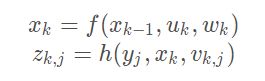
xk表示机器人当前所处的位置，uk是运动传感器的读数或者输入，zkj是机器人与环境特征建立的观测数据
另外，无论是位置方程还是观测方程均要引入噪声，也就是式子中的w和v，也因此需要在后端进行优化，或者说状态估计，来找到一个最有可能的位姿图。
可以参照下图有一个更加清楚地认识

编程基础Linux

可以参照我的另一篇博文，记录了Linux最基本的操作指令，对于初学者可以减少学习负担
Linux基本知识学习笔记（常用指令）

使用Cmake

该部分还不是很了解，可以简单理解为会有一个CmakeList来帮助工程判断如何编译
在Linux中，当我们写完源代码后，需要通过编译，将多文件工程建立联系，并生成可执行文件，以此来实现调试运行，Cmake则可以为工程生成一个makefile文件，之后使用make命令（C++库使用g++进行编译）根据makefile文件中的内容编译整个工程
在书中简单介绍了自己使用命令行及cmake建立工程并运行的例子，比较有意思

第三讲 三维空间的刚体运动

• 本讲目标：理解刚体运动描述方式、旋转矩阵、变换矩阵、四元数和欧拉角
• 掌握Eigen库的矩阵，几何模块的使用方法

3.1 点、向量和坐标系，旋转矩阵

• 点存在于三维空间中
• 点和电可以组成向量
• 点本身由原点指向它的向量描述

向量：带指向的箭头，可以进行加法减法等运算
向量的坐标：可以用R3坐标表示
坐标系：由三个正交的轴组成
构成线性空间的一组基
分为左手系和右手系
向量运算：加减法，内积，外积
关于外积，引入了小尖^，表示将一个向量变成一个矩阵
在SLAM中：

• 有固定的世界坐标系和移动的机器人坐标系
• 机器人坐标系随着机器人的运动而改变，每个时刻都有新的坐标系

两个坐标系如何变换？原点间的平移和三个轴的旋转
旋转矩阵：
充分必要条件：

• R是一个正交矩阵，矩阵的逆等于转置
• R的行列式为1

三维空间旋转：SO(3) 也成为特殊正交群，群的概念在李代数再探讨
用四个数描述三维坐标，可以实现同时表示平移和旋转。
这种做法称为齐次坐标。
此时旋转和平移可以放入一个矩阵，称为变换矩阵。

旋转矩阵与变换矩阵如下（非齐次形式）

3.3 欧拉角

欧拉角描述了刚体围绕三个轴旋转的角度
不同的旋转顺序对应不同的欧拉角，常用的是ZYX顺序，即“偏航-俯仰-滚转”
欧拉角存在万向锁问题，可能会在一些情况下失去一个自由度
对于万向锁问题，可以拿手机测试（或者任何物体），一旦有绕一个轴±90度旋转，那么其余两轴的作用效果将相同，失去了一个维度的信息，很有意思。

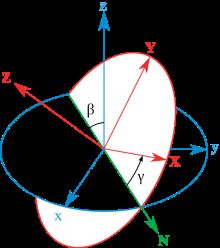
事实上，我们找不到不带奇异性的三维向量描述方式
所以用四元数这个四个维度的描述方式来表示旋转

3.4 四元数

一种扩展的复数
四元数有三个虚部，可以表达三维空间的旋转
虚部之间有特定的运算关系，有点想三维空间中的叉积
四元数有很多特定的公式，包括四元数的逆（对于表述旋转很重要）

注意： Eigon库中对四元数乘法进行了重载，不必写出四元数的逆，运算符重载自动完成了这一步。

第四讲 李群和李代数

研究李群和李代数的根本目的：

1. 将旋转矩阵变为可以加减的形式
2. 消除后端优化中的约束问题

通过李群—李代数之间的转换关系，希望把位姿估计变成无约束的优化问题。

李群和李代数基础

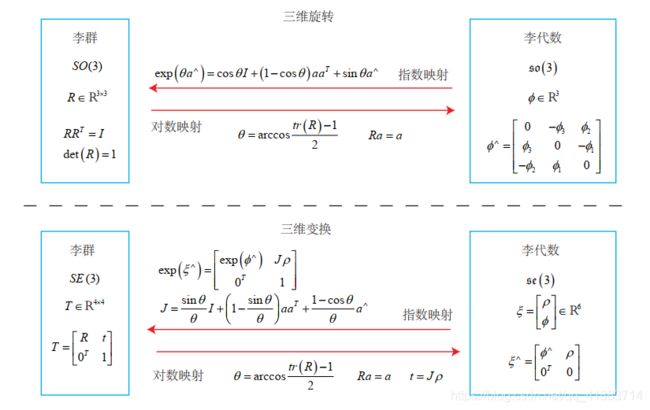
我们之前接触了两个群：

• 特殊正交群：SO(3) 三维空间的旋转矩阵，是一个正交矩阵，且行列式为1，则为旋转矩阵
• 特殊欧式群：SE(3) 包含三维空间旋转矩阵R，平移向量t，0^T和1的四维空间变换矩阵，即为三维欧式变换群

群（group）：是一种集合加上一种运算的代数结构，这个运算要满足“封结幺逆”四个条件

• 封闭性
• 结合律
• 幺元
• 逆

李群（Lie Group）：是指具有连续（光滑）性质的群
反对称矩阵：对于一个向量，可以将其变成反对称矩阵，对于任意的反对称矩阵，也可以找到一个与之对应的向量，具体表示符号及含义如下图

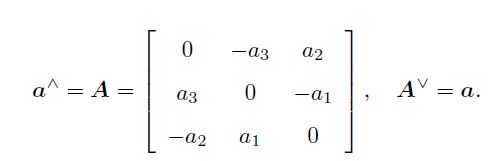
李代数Φ：它是SO(3)在原点附近的正切空间，有如下的近似计算公式，对旋转矩阵求导相当于左乘一个李代数反对称矩阵，旋转矩阵等于e的李代数反对称矩阵次幂

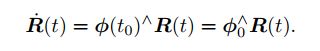
李代数由一个集合、一个数域、一个二元运算组成，如果他们满足以下几个特征，就称(V,F,[,])为一个李代数，记为g

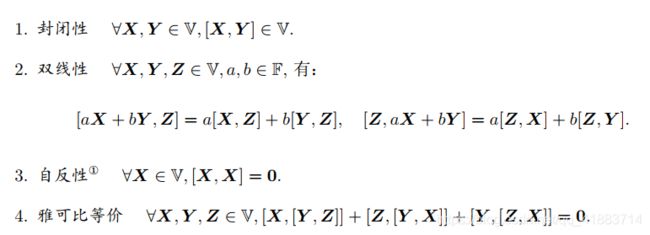
需要明确的是，李代数不加区分的表示三维向量及其反对称矩阵，如下公式可以看出这一点

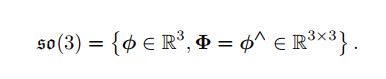
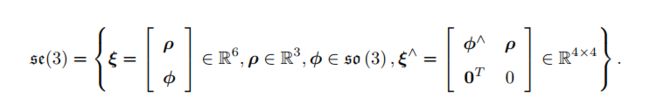
指数映射：在李群和李代数中，计算exp(Φ^)称为指数映射（Exponential Map）
对于某一个时刻（这很重要，不考虑时间t的影响），以SO(3)为例，有如下的等式成立

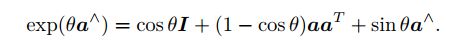
等式左边就是某个时刻的旋转矩阵（公式推导中本来是有一个t的），同时我们将李代数Φ等效为θa，θ为模长，a为长度为1的方向向量
特别的，上式和罗德里格斯公式如出一辙，这表明李代数so(3)实际上就是由所谓的旋转向量组成的空间，而指数映射即为罗德里格斯公式。
通过它们，我们将李代数so(3)中的任意一个向量对应到了一个位于李群SO(3)中的旋转矩阵。反之定义对数映射

对数映射：指数映射的逆过程，公式如下

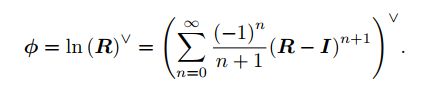
李群和李代数相互转化关系由如下关系图表示

**李代数求导问题：**在求解最优估计的时候，我们经常会构建与位姿有关的函数，然后讨论该函数关于位姿的导数，以调整当前的估计值。
李代数求导思路：

• 用李代数表示姿态，然后根据李代数加法对李代数求导
• 对李群左乘或右乘微小扰动，然后对该扰动求导，称为左扰动和右扰动模型。

直接对李代数求导，结果如下，因为含有形式较为复杂的Jl，我们不喜欢该表示形式。

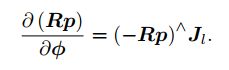
扰动模型求导，结果如下，需要理解下述公式，比较重要

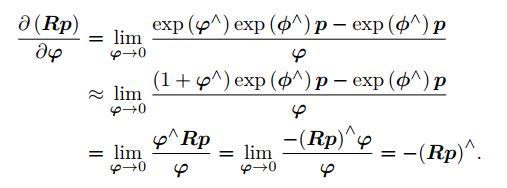
实践Sophus

有待补充

第五讲 相机与图像

相机模型

相机将三维世界中的坐标点（单位为米）映射到二维图像平面（单位为像素）的过程，并能够使用一个几何模型进行描述。
其中最常用的为针孔模型。
另外，这里涉及到几个坐标系的转换关系。

四个坐标系：

世界坐标系–相机坐标系–图像坐标系–像素坐标系
世界坐标系：人为定义的一种最原始的基础坐标系，用来描述世界中各个物体所处的位置
相机坐标系：以相机光心为原点，相机自身的坐标系，是一个三维坐标系
图像坐标系：在相机的成像平面上，为了描述相机坐标系的成像情况，所建立的二维坐标系
像素坐标系：以成像平面左上角为原点，像素大小为坐标分度值，将图像坐标系上的图像转化为像素坐标信息，是最终获得图片的二维坐标系

针孔相机模型

针孔相机模型示意图如图所示

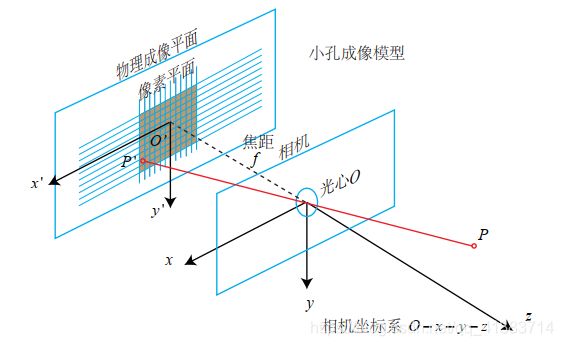
世界坐标系到相机坐标系：
从自定义的世界坐标系完成一次平移加旋转
相机坐标系到图像坐标系：
利用投影关系，根据相似定理，找到一种投影比例关系
图像坐标系到像素坐标系：
由于坐标尺度和原点不同，要进行伸缩和平移

有意思的是：我们利用单目相机拍摄时，会损失掉深度信息，这在计算过程中的归一化过程有所体现，从物理层面上来理解，只要一个物体的投影点保持不变，是可以在空间中任意遥远的距离移动，或者说近处的小物体和远处的大物体看起来可以完全相同

畸变模型

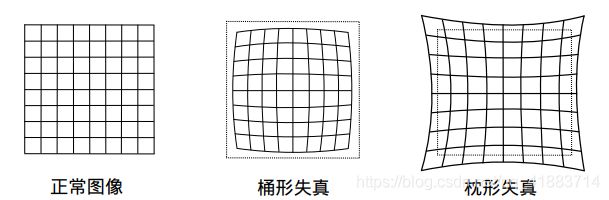
畸变分类：

• 径向畸变：由透镜形状引起的畸变：桶形畸变&枕形畸变
• 切向畸变：透镜和成像面未严格平行引入的畸变

实践部分

有待补充