LeetCode题库:并查集问题(Python语言实现)
并查集相关知识
并查集常用模板
class UnionSet:
def init_tree(self,n):
self.fa = [i for i in range(n)] # 必要,记录根节点,也可能是字典形式
self.cnt = collections.defalutdict(lambda :1) # 不一定必要,用于计算树的高度
def find(self,x): # 寻找根节点,并状态压缩
while self.fa[x]!=x:
x= self.fa[x]
return x
def union(self,u,v): # 合并
ru = self.find(u)
rv = self.find(v)
if ru == rv:
return
self.fa[ru] = rv
return
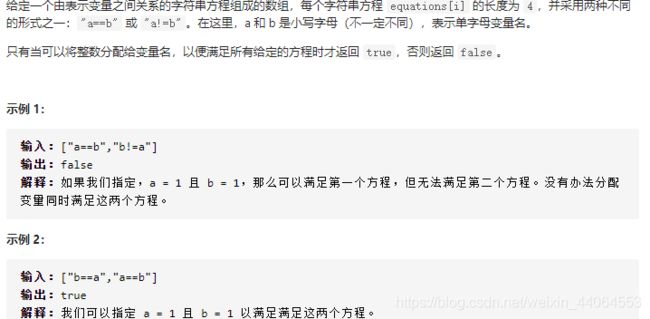
1、LeetCode900、等式方程的可满足性
题目描述
题解思路
- 等式具有传递性,将a-z映射成0-25一共26个数字
- 遍历所有的等式,将等式左右两边的字母(已经转换成数字了)连通起来
- 遍历所有的不等式,如果等式左右两边字母的根节点一样,与不等这个条件矛盾,返回False
- 遍历结束,返回True
python代码
class Solution:
# 并查集,等式具有传递性
def init_tree(self,n):
self.fa = [i for i in range(n)]
def find(self,x):
while self.fa[x]!=x:
x= self.fa[x]
return x
def union(self,u,v):
ru = self.find(u)
rv = self.find(v)
if ru == rv:
return
self.fa[ru] = rv
return
def equationsPossible(self, equations: List[str]) -> bool:
self.init_tree(26) # 初始化并查集
for s in equations: # 遍历等式
if s[1] == '=':
index1 = ord(s[0])-ord('a')
index2 = ord(s[3])-ord('a')
self.union(index1,index2)
for s in equations: # 遍历不等式
if s[1] == '!':
index1 = ord(s[0])-ord('a')
index2 = ord(s[3])-ord('a')
if self.find(index1) == self.find(index2):
return False
return True
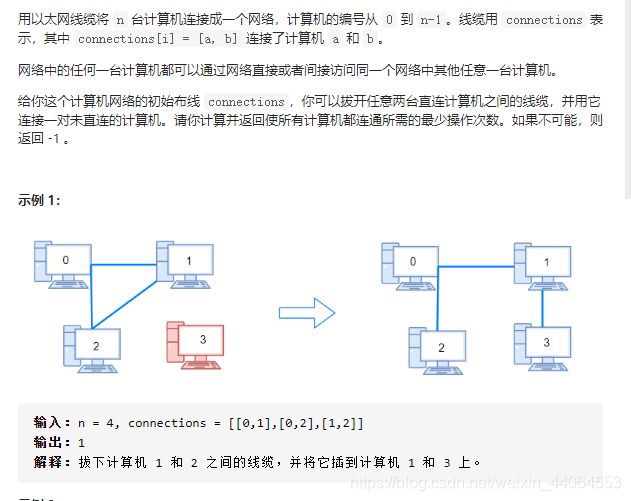
2、LeetCode1319、连通网络的操作次数
题目描述
题解思路
- 总共需要n-1个线缆
- 如果两个计算机的根节点一样,可以节省一根线
- 判断还需要的线缆数目和省下来的线缆的数目,如果后者大,返回前者,否则返回-1
Python代码
class Solution:
def init_tree(self,n):
self.fa = [i for i in range(n)]
def find(self,x):
while self.fa[x]!=x:
x= self.fa[x]
return x
def union(self,u,v):
ru = self.find(u)
rv = self.find(v)
if ru == rv:
return
self.fa[ru] = rv
return
def makeConnected(self, n: int, connections: List[List[int]]) -> int:
# 总共需要n-1个线缆
# 如果两个计算机的跟节点一样,可以省一根线,假设省x根
# if (n-1)-(len(connections)-x)>x:return -1 else return 前面的部分
self.init_tree(n)
x = 0
for s in connections:
if self.find(s[0])!=self.find(s[1]):
self.union(s[0],s[1])
else:
x+=1
res = (n-1)-(len(connections)-x)
return res if res<=x else -1
可以看到基本上并查集部分的模板代码是几乎不怎么需要改变的!!!
3、LeetCode684、冗余连接
题目描述
题解思路
- 遍历节点,如果一条边的两个顶点的根节点不一样,就进行合并
- 如果一样,说明已经形成环了,直接返回(如示例1,节点2和3的根节点都是1,而[2,3]表示的又是2,3之间有边,所以已经成环了)
Python代码
class Solution:
# 并查集
# 遍历节点,如果一条边的两个顶点的父节点不一样,就合并;
# 如果一样,说明形成环了,直接返回
def init_tree(self,n):
self.fa = [i for i in range(n)]
def find(self,x):
while self.fa[x]!=x:
x= self.fa[x]
return x
def union(self,u,v):
ru = self.find(u)
rv = self.find(v)
if ru == rv:
return
self.fa[ru] = rv
return
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
n = len(edges)
self.init_tree(n)
for i in range(n): # 调用find函数要注意find中的索引应该是[0,len(self.fa)-1]
if self.find(edges[i][0]-1) != self.find(edges[i][1]-1): # 因为self.fa=[1,2,3],但是索引从0开始
self.union(edges[i][0]-1,edges[i][1]-1)
else:
return edges[i]
return -1
4、LeetCode128、最长连续子序列
题目描述
题解思路
- 除了要初始化根节点以外,还要初始化每个根节点对应的树的高度
- 并查集的连接函数需要修改一下,即要有具体的返回值,如果两棵树的根节点一样,就将两个数的高度加起来,并返回
- 遍历数组,迭代更新当前数与(当前数+1)的连接结果
Python代码
class Solution:
def init_tree(self,nums):
self.fa = {
num:num for num in nums}
self.cnt = collections.defaultdict(lambda:1)
def find(self,x):
while self.fa[x]!=x:
x = self.fa[x]
return x
def union(self,u,v):
if v not in self.fa:
return 1
ru = self.find(u)
rv = self.find(v)
if ru == rv:
return self.cnt[ru]
self.fa[ru] = rv
self.cnt[rv]+=self.cnt[ru]
return self.cnt[rv]
def longestConsecutive(self, nums: List[int]) -> int:
# 方法1、模拟
# nums = list(set(nums))
# nums.sort()
# index = 0
# count = 1 # 记录连续序列长度
# res = 0 # 记录结果
# while index
# if nums[index]+1 in nums:
# count+=1
# else:
# count = 1 # 不连续,就重头开始计数
# res = max(res,count)
# index+=1
# return res
# 方法2,并查集
n = len(nums)
res = 0
self.init_tree(nums)
for num in nums:
res = max(res,self.union(num,num+1))
return res
注意到这里初始化并查集的根节点,使用的是哈希表而不是数组,因为给定的数字数组并不是连续的
5、LeetCode947、移除最多的同行同列的石头
题目描述
1 <= stones.length <= 1000
0 <= xi, yi <= 10**4
不会有两块石头放在同一个坐标点上
题解思路
- 可以给nums中每个坐标定义一个索引,然后如果两个坐标含有相同的横纵坐标,就连通两个坐标
- 最后查看有几个独立的并查集集合,也就是最终留下的坐标个数x
- 返回len(nums)-x即可
Python代码
class Solution:
def init_tree(self,n):
self.fa = [i for i in range(n)]
def find(self,x):
while self.fa[x]!=x:
x= self.fa[x]
return x
def union(self,u,v):
ru = self.find(u)
rv = self.find(v)
if ru == rv:
return
self.fa[ru] = rv
return
def removeStones(self, stones: List[List[int]]) -> int:
self.init_tree(len(stones))
for i in range(len(stones)-1):
for j in range(i+1,len(stones)):
if stones[i][0]==stones[j][0] or stones[i][1]==stones[j][1]:
self.union(i,j)
hashmap = {
}
for i in range(len(stones)):
hashmap[i] = self.find(i)
return len(stones)-len(set(hashmap.values()))
但是此种方法时间复杂度较高,需要两次遍历,还可以继续优化
实际上,只需要将每个点的横纵坐标连通起来就可以了,但是并查集是一个一维的数据结构,横坐标=2,显然和纵坐标=2是不一样的2,于是为了区分,考虑到横纵坐标的取值范围,将纵坐标+1000即可
class Solution:
def init_tree(self,n):
self.fa = [i for i in range(n)]
def find(self,x):
while self.fa[x]!=x:
x= self.fa[x]
return x
def union(self,u,v):
ru = self.find(u)
rv = self.find(v)
if ru == rv:
return
self.fa[ru] = rv
return
def removeStones(self, stones: List[List[int]]) -> int:
self.init_tree(20000)
for x,y in stones:
self.union(x,y+10000) # 并查集是一维的,比如第二行和第二列可能难以区分,故将列+10000转换为一维的
return len(stones)-len({
self.find(x) for x,y in stones}) # {}表示集合,自动去重
6、LeetCode547、省份数量
题目描述
题解思路
- 连接相连的两个城市
- 遍历数组,没连接成功一个,独立的省份数量就少一个
Python代码
class Solution:
# 并查集
def init_tree(self, n) -> None:
self.fa = [i for i in range(n)] # 记录每个节点的父节点
def find(self, x):
while self.fa[x] != x:
x = self.fa[x]
return x
def union(self, u, v):
ru = self.find(u)
rv = self.find(v)
if ru == rv:
return False
self.fa[ru] = rv # 将ru的根设为rv
return True
def findCircleNum(self, M: List[List[int]]) -> int:
n = len(M)
self.init_tree(n)
res = n
for i in range(n):
for j in range(i + 1, n):
if M[i][j] == 1 and self.union(i, j):
res -= 1
return res
这里不同的是连接函数中,返回了True和False
带权重的并查集不会,懒得看,看不懂,暂且PASS