机器学习西瓜书吃瓜笔记之(二)决策树分类 附一键生成决策树&可视化python代码实现

决策树分类（附一键生成可视化python代码实现）

决策树

• 决策树是用于分类任务的树结构，它的叶子结点为类别，其余节点为判断操作。

• 决策树类似于日常中判断分类的方法。对某个样本进行分类时：

  1. 从根节点开始
  2. 得到所处节点的判断结果
  3. 移动到满足结果的子节点上
  4. 当移动到叶子结点上时，返回类别，否则转第2步
     

• 研究决策树，重点在于如何构建决策树。

构建

决策树学习基本算法：

输入:
    训练集 D={(X1,y1),(X2,y2),...,(Xm,ym)}
    属性集 A={a1,a2,...,ad}
过程:函数 TreeGenerate(D,A)
    生成结点 node;
    if D中样本全属于同一类别C then
        将node标记为C类叶结点; return
    end if
    if A=∅ or D中样本在A上取值相同 then
        将node标记为叶结点,其类别标记为D中样本数最多的类; return
    end if

    从A中选择最优划分属性a*;

    for a* 的每一个值 a*_v do
        为node生成一个分支; 令Dv表示D中在a*上取值为a*_v的样本子集;
        if Dv 为空 then
            将分支结点标记为叶结点,其类别标记为D中样本最多的类; return
        else
            以TreeGenerate(D, A \ {a*})为分支结点
        end if
    end for
输出:以node为根结点的一棵决策树

算法中最关键的是如何从$A$中选择最优划分属性$a^{\ast }$，不同的划分选择决定了决策树的种类：

1. 信息增益 ⇒ ID3决策树
2. 信息增益率 ⇒ C4.5决策树
3. 基尼指数 ⇒ CART决策树

信息熵

通俗理解信息熵 - 知乎
信息熵是度量样本集合纯度最常用的指标。假定当前样本集合$D$中第$i$类样本所占比例为$p_i(i=1,2,\cdots ,n)$，则$D$的信息熵定义为：
$$H(X)=-\sum _{i=1}^{n}p(x_i)\cdot logp(x_i)$$

• 越小概率的事情发生了产生的信息量越大
• 熵则是在结果出来之前对可能产生的信息量的期望
• 信息熵描述随机变量的不确定性，信息熵越小，数据集不确定性就低

条件熵

通俗理解条件熵 - 知乎
条件熵代表在某一个条件下，随机变量的复杂度（不确定度）
$$\begin{array}{rl}H(Y|X)& =-\sum _{x\in X}p(x)\cdot H(Y|X=x)\\ & =-\sum _{x\in X}p(x)\sum _{y\in Y}p(y|x)\cdot logp(y|x)\\ & =-\sum _{x\in X}\sum _{y\in Y}p(x,y)logp(y|x)\end{array}$$

• 条件熵是指在给定某个变量为某个值的情况下，另一个变量的熵是多少
• 在每一个小类里面，都计算一个小熵，然后每一个小熵乘以各个类别的概率，然后求和，得到条件熵

信息增益

X的熵减去Y条件下X的熵，就是信息增益：
$$Gain(X,Y)=H(X)-H(Y|X)$$

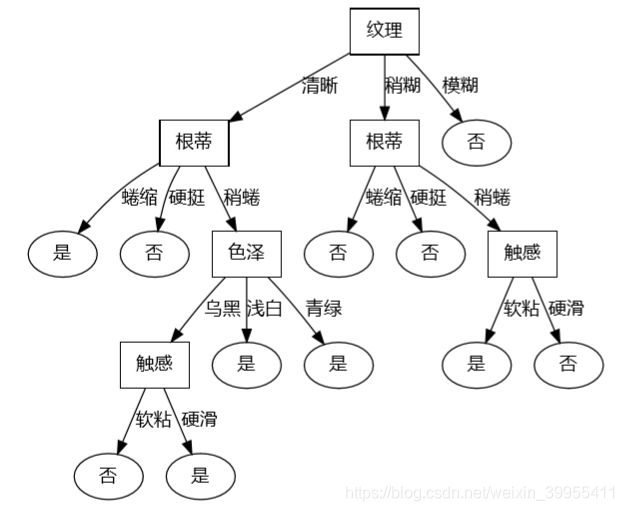
决策树生成&可视化

• 直接复制粘贴就可以运行看结果，说不清楚的地方请看我的代码具体实现，关键部分已经全部加上注释。
• 可视化部分需要安装graphviz包，具体请百度安装教程(pip一下,官网下载release版本解压再把路径加环境path就行了)。
• 要是可视化报错Error: Could not open "decisionTree.gv.pdf" for writing : Invalid argument'记得在浏览器关闭之前的视图

from random import choice
from collections import Counter
import math

# ==========
# 定义数据集
# ==========
D = [
    {
     '色泽': '青绿', '根蒂': '蜷缩', '敲声': '浊响', '纹理': '清晰', '脐部': '凹陷', '触感': '硬滑', '好瓜': '是'},
    {
     '色泽': '乌黑', '根蒂': '蜷缩', '敲声': '沉闷', '纹理': '清晰', '脐部': '凹陷', '触感': '硬滑', '好瓜': '是'},
    {
     '色泽': '乌黑', '根蒂': '蜷缩', '敲声': '浊响', '纹理': '清晰', '脐部': '凹陷', '触感': '硬滑', '好瓜': '是'},
    {
     '色泽': '青绿', '根蒂': '蜷缩', '敲声': '沉闷', '纹理': '清晰', '脐部': '凹陷', '触感': '硬滑', '好瓜': '是'},
    {
     '色泽': '浅白', '根蒂': '蜷缩', '敲声': '浊响', '纹理': '清晰', '脐部': '凹陷', '触感': '硬滑', '好瓜': '是'},
    {
     '色泽': '青绿', '根蒂': '稍蜷', '敲声': '浊响', '纹理': '清晰', '脐部': '稍凹', '触感': '软粘', '好瓜': '是'},
    {
     '色泽': '乌黑', '根蒂': '稍蜷', '敲声': '浊响', '纹理': '稍糊', '脐部': '稍凹', '触感': '软粘', '好瓜': '是'},
    {
     '色泽': '乌黑', '根蒂': '稍蜷', '敲声': '浊响', '纹理': '清晰', '脐部': '稍凹', '触感': '硬滑', '好瓜': '是'},
    {
     '色泽': '乌黑', '根蒂': '稍蜷', '敲声': '沉闷', '纹理': '稍糊', '脐部': '稍凹', '触感': '硬滑', '好瓜': '否'},
    {
     '色泽': '青绿', '根蒂': '硬挺', '敲声': '清脆', '纹理': '清晰', '脐部': '平坦', '触感': '软粘', '好瓜': '否'},
    {
     '色泽': '浅白', '根蒂': '硬挺', '敲声': '清脆', '纹理': '模糊', '脐部': '平坦', '触感': '硬滑', '好瓜': '否'},
    {
     '色泽': '浅白', '根蒂': '蜷缩', '敲声': '浊响', '纹理': '模糊', '脐部': '平坦', '触感': '软粘', '好瓜': '否'},
    {
     '色泽': '青绿', '根蒂': '稍蜷', '敲声': '浊响', '纹理': '稍糊', '脐部': '凹陷', '触感': '硬滑', '好瓜': '否'},
    {
     '色泽': '浅白', '根蒂': '稍蜷', '敲声': '沉闷', '纹理': '稍糊', '脐部': '凹陷', '触感': '硬滑', '好瓜': '否'},
    {
     '色泽': '乌黑', '根蒂': '稍蜷', '敲声': '浊响', '纹理': '清晰', '脐部': '稍凹', '触感': '软粘', '好瓜': '否'},
    {
     '色泽': '浅白', '根蒂': '蜷缩', '敲声': '浊响', '纹理': '模糊', '脐部': '平坦', '触感': '硬滑', '好瓜': '否'},
    {
     '色泽': '青绿', '根蒂': '蜷缩', '敲声': '沉闷', '纹理': '稍糊', '脐部': '稍凹', '触感': '硬滑', '好瓜': '否'},
]


# ==========
# 决策树生成类
# ==========
class DecisionTree:
    def __init__(self, D, label, chooseA):
        self.D = D  # 数据集
        self.label = label  # 哪个属性作为标签
        self.chooseA = chooseA  # 划分方法
        self.A = list(filter(lambda key: key != label, D[0].keys()))  # 属性集合A
        # 获得A的每个属性的可选项
        self.A_item = {
     }
        for a in self.A:
            self.A_item.update({
     a: set(self.getClassValues(D, a))})
        self.root = self.generate(self.D, self.A)  # 生成树并保存根节点

    # 获得D中所有className属性的值
    def getClassValues(self, D, className):
        return list(map(lambda sample: sample[className], D))

    # D中样本是否在A的每个属性上相同
    def isSameInA(self, D, A):
        for a in A:
            types = set(self.getClassValues(D, a))
            if len(types) > 1:
                return False
        return True

    # 构建决策树，递归生成节点
    def generate(self, D, A):
        node = {
     }  # 生成节点
        remainLabelValues = self.getClassValues(D, self.label)  # D中的所有标签
        remainLabelTypes = set(remainLabelValues)  # D中含有哪几种标签

        if len(remainLabelTypes) == 1:
            # 当前节点包含的样本全属于同个类别，无需划分
            return remainLabelTypes.pop()  # 标记Node为叶子结点,值为仅存的标签

        most = max(remainLabelTypes, key=remainLabelValues.count)  # D占比最多的标签

        if len(A) == 0 or self.isSameInA(D, A):
            # 当前属性集为空，或是所有样本在所有属性上取值相同，无法划分
            return most  # 标记Node为叶子结点,值为占比最多的标签

        a = self.chooseA(D,A,self)  # 划分选择

        for type in self.A_item[a]:
            condition = (lambda sample: sample[a] == type)  # 决策条件
            remainD = list(filter(condition, D))  # 剩下的样本
            if len(remainD) == 0:
                # 当前节点包含的样本集为空，不能划分
                node.update({
     type: most})  # 标记Node为叶子结点,值为占比最多的标签
            else:
                # 继续对剩下的样本按其余属性划分
                remainA = list(filter(lambda x: x != a, A))  # 未使用的属性
                _node = self.generate(remainD, remainA)  # 递归生成子代节点
                node.update({
     type: _node})  # 把生成的子代节点更新到当前节点
        return {
     a: node}


# ==========
#  定义划分方法
# ==========

# 随机选择
def random_choice(D, A, tree: DecisionTree):
    return choice(A)

# 信息熵
def Ent(D,label,a,a_v):
    D_v = filter(lambda sample:sample[a]==a_v,D)
    D_v = map(lambda sample:sample[label],D_v)
    D_v = list(D_v)
    D_v_length = len(D_v)
    counter = Counter(D_v)
    info_entropy = 0
    for k, v in counter.items():
        p_k = v / D_v_length
        info_entropy += p_k * math.log(p_k, 2)
    return -info_entropy

# 信息增益
def information_gain(D, A, tree: DecisionTree):
    gain = {
     }
    for a in A:
        gain[a] = 0
        values = tree.getClassValues(D, a)
        counter = Counter(values)
        for a_v,nums in counter.items():
            gain[a] -= (nums / len(D)) * Ent(D,tree.label,a,a_v)
    return max(gain.keys(),key=lambda key:gain[key])

# ==========
#  创建决策树
# ==========
desicionTreeRoot = DecisionTree(D, label='好瓜',chooseA=information_gain).root
print('决策树:', desicionTreeRoot)


# ==========
# 决策树可视化类
# ==========
class TreeViewer:
    def __init__(self):
        from graphviz import Digraph
        self.id_iter = map(str, range(0xffff))
        self.g = Digraph('G', filename='decisionTree.gv')

    def create_node(self, label, shape=None):
        id = next(self.id_iter)
        self.g.node(name=id, label=label, shape=shape, fontname="Microsoft YaHei")
        return id

    def build(self, key, node, from_id):
        for k in node.keys():
            v = node[k]
            if type(v) is dict:
                first_attr = list(v.keys())[0]
                id = self.create_node(first_attr+"？", shape='box')
                self.g.edge(from_id, id, k, fontsize = '12', fontname="Microsoft YaHei")
                self.build(first_attr, v[first_attr], id)
            else:
                id = self.create_node(v)
                self.g.edge(from_id, id, k, fontsize = '12', fontname="Microsoft YaHei")

    def show(self, root):
        first_attr = list(root.keys())[0]
        id = self.create_node(first_attr+"？", shape='box')
        self.build(first_attr, root[first_attr], id)
        self.g.view()


# ==========
# 显示创建的决策树
# ==========
viewer = TreeViewer()
viewer.show(desicionTreeRoot)

敲代码不易，且用且珍惜，若要转载请注明出处，谢谢