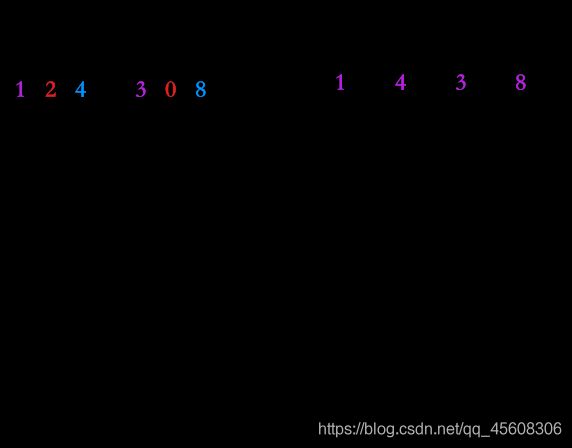排序算法合集及其应用举例
1. 排序算法一表总览
| 排序算法 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂的 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 快速排序 | O ( n log n ) O(n\log n) O(nlogn) | O ( n 2 ) O(n^2) O(n2) | O ( n log n ) O(n\log n) O(nlogn) | O ( log n ) O(\log n) O(logn) | 交换 | 不稳定 |
| 计数排序 | O ( k + n ) O(k + n) O(k+n) | O ( k + n ) O(k + n) O(k+n) | O ( k + n ) O(k + n) O(k+n) | O ( k + n ) O(k + n) O(k+n) | \ | 稳定 |
| 堆排序 | O ( n log n ) O(n\log n) O(nlogn) | O ( n log n ) O(n\log n) O(nlogn) | O ( n log n ) O(n\log n) O(nlogn) | O ( 1 ) O(1) O(1) | 选择 | 不稳定 |
| 归并排序 | O ( n log n ) O(n\log n) O(nlogn) | O ( n log n ) O(n\log n) O(nlogn) | O ( n log n ) O(n\log n) O(nlogn) | O ( n ) O(n) O(n) | \ | 稳定 |
| 希尔排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( n 1.3 ) O(n^{1.3}) O(n1.3) | O ( 1 ) O(1) O(1) | 插入 | 不稳定 |
| 插入排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 插入 | 稳定 |
| 冒泡排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 交换 | 稳定 |
| 选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 选择 | 稳定 |
其他注意事项:
- 计数排序中, k k k是整数的范围
- 稳定性是指,序列中相同的数是否有可能交换顺序,例如序列中有两个8,顺序为 8 8 8和 8 ′ 8^{'} 8′,如果在排序完之后,顺序有可能变为 8 ′ 8^{'} 8′和 8 8 8,那么这种排序就是不稳定的排序算法;若不可能改变顺序,则是稳定算法。
- 只有归并排序可用于外部排序
- 在下面的代码中,swap函数用于元素交换,实现为:
private static void swap(int nums, int i, int j){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
2. 各排序算法说明及其实现
2.1 快速排序
-
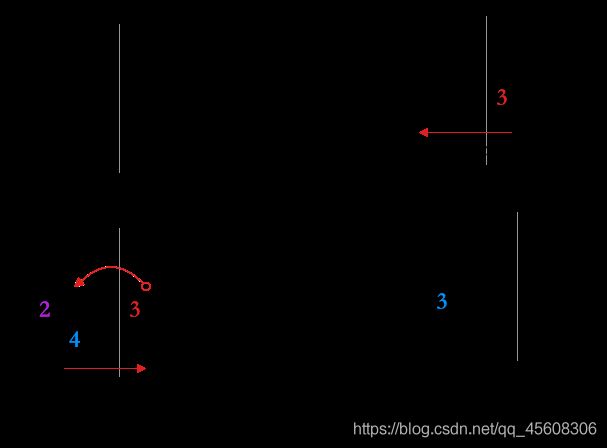
原理:选择一个轴元素key,通过 i j ij ij指针定位元素,将待排序数组分为左侧小于等于key和右边大于等于key两组,递归操作。
-
时间复杂度:二分思想,故平均复杂度 O ( n log n ) O(n \log n) O(nlogn);但如果每次二分选择的轴都极不平均则更高,极端举例:只把元素分为1和 n − 1 n-1 n−1个,则出现需要划分n次,而每次都要遍历数组,因此最坏复杂度为 O ( n 2 ) O(n^2) O(n2)。例如完全正序,完全逆序都将出现最坏情况
-
空间复杂度:只有轴需要消耗空间,而二分法,每个部分都需要一个轴,因此空间为 O ( log n ) O(\log n) O(logn)
-
稳定性:根据图示可知,当 i j ij ij都定位到轴元素key时,将发生位置交换,因此不具有稳定性
-
参考代码
public static void quickSort(int[] nums, int l, int r){
if(l >= r) return;
int i = l - 1, j = r + 1; //先定位到边界两侧
int key = nums[l];
while(i < j){
while(nums[++i] < key); //先移动再与关键字判断
while(nums[--j] > key); //先移动在与关键字判断
if(i < j)
swap(nums, i, j); //交换两侧值
}
quickSort(nums, l, j);
quickSort(nums, j + 1, r);
}
2.2 堆排序
- 图示:较为复杂,暂无
- 原理:建立大顶堆,循环 n n n次,每次:交换堆顶元素与堆尾元素使得堆中最大元素归于排序的正确位置,之后通过向下调整堆来完成堆的重构。
- 时间复杂度:每次调整堆显然需要经过树高 h = log n h = \log n h=logn次比较,总共有 n n n个数,需要进行 n n n轮次调整堆,因此复杂度为 O ( n log n ) O(n \log n) O(nlogn)。另外,通过向下调整建堆时间复杂度也是 O ( n log n ) O(n \log n) O(nlogn),而若通过向上调整建堆时间复杂度可将降到 O ( n ) O(n) O(n)
- 空间复杂度:消耗常数个空间用于存放比较时的临时变量
- 稳定性:堆尾元素会被放到堆顶用于向下调整,而无论向下调整堆是怎样的比较方案,都无法保证相同的元素不会被交换其原有位置。
- 参考代码
public static void heapSort(int[] nums){
for (int i = (nums.length >>> 1) - 1; i >= 0; i--){
//建堆
siftDown(nums, i, nums.length);
}
for(int i = nums.length - 1; i > 0; i--){
//排序
swap(nums, 0, i);
siftDown(nums, 0, i);
}
}
private static void siftDown(int[] heap, int i, int len){
int curNum = heap[i];
int half = len >>> 1;
while (i < half){
//直到到没有子结点
int lcIdx = (i << 1) + 1; //左子结点索引
int rcIdx = lcIdx + 1; //右子结点索引
int temp = heap[lcIdx]; //选取左子结点作为临时值
if(rcIdx < len && temp < heap[rcIdx]){
temp = heap[lcIdx = rcIdx];
}
if (curNum >= temp)
break;
heap[i] = temp;
i = lcIdx; //下一层检测
}
heap[i] = curNum;
}
2.2 归并排序
-
原理:对于已排好序的两个数组合并,只需要通过两个数组各自的指针 i j ij ij进行遍历,将比较结果放入新数组中,之后移动指针即可。归并排序通过上述理论,首先将数组两两划分,直到划分到长为1(有序),之后两两合并完成操作。
-
时间复杂度:典型分治,时间复杂度 O ( n log n ) O(n \log n) O(nlogn)
-
空间复杂度:合并时开辟一个存放合并结果的辅助数组,数组长度只需要和原数组长度一致即可,因此为 O ( n ) O(n) O(n)
-
稳定性:合并时不会影响次序,具有稳定性
-
参考代码
public void mergeSort(int nums, int l, int r){
if(l >= r) return;
int mid = (l + r) >> 1;
mergeSort(nums, l, mid);
mergeSort(nums. mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r){
if (nums[i] <= nums[j])
temp[k++] = nums[i++];
else
temp[k++] = nums[j++];
}
//temp是外部开好的数组
while (i <= mid) temp[k++] = nums[i++];
while (j <= r) temp[k++] = nums[j++];
for (i = l, j = 0; i <= r; i++, j++)
nums[i] = temp[j];
}
2.2 选择排序
-
原理:一轮遍历可以找到一个数组的最小值,选择排序的方式就是每一轮都找到一个数组的最小值,是最容易理解的排序方法。
-
时间复杂度:需要 n / 2 n/2 n/2次遍历,每次遍历平均需要搜索 n / 2 n/2 n/2个元素,因此,时间复杂度 O ( n ) O(n) O(n)
-
空间复杂度:需要常数辅助空间作为比较元素的临时遍历
-
稳定性:每次选择都是从前往后选,因此可以是稳定的
-
参考代码
public static void selectSort(int nums){
for(int i = 0; i < nums.length; i++){
int idx = i;
for(int j = i; j < nums.length; j++){
if(nums[j] < nums[i])
idx = j;
}
swap(nums, i, idx);
}
}
2.2 插入排序
-
原理:在排好顺中的序列中,可以通过遍历找到某个待插入正确位置使得新数组是有序的,因此,插入排序从前往后,依次将元素插入已排好序的数组中即可。(一个元素的数组可以看作有序数组)
-
时间复杂度:查找元素和插入平均都需要 n / 2 n/2 n/2次操作,因此,时间复杂度 O ( n 2 ) O(n^2) O(n2);若数组已经升序,则只需要进行 n − 1 n-1 n−1次比较,因此最好时间复杂度为 O ( n ) O(n) O(n),二分查找优化可降到 O ( log n ) O(\log n) O(logn)
-
空间复杂度:比较后插入时需要常数个辅助空间存放临时变量
-
稳定性:可以是稳定的,设置好比较方法使得相同时插入在后面即可
-
参考代码
public static void insertSort(int nums){
for(int i = 1; i < nums.length; i++){
int temp = nums[i];
for(int j = i; j > 0 && nums[j - 1] > temp; j--){
nums[j] = nums[j - 1];
}
nums[j] = temp;
}
}
- 二分查找插入排序(即查找插入位置时使用二分法优化)
public static void insertSort(int nums){
for(int i = 1; i < nums.length; i++){
int temp = nums[i];
int l = 0, r = i - 1;
while(l <= r){
int mid = (l + r)/2;
if(nums[mid] > temp) r = mid - 1;
else l = mid + 1;
}
for(int j = i; j > low; j--){
nums[j] = nums[j - 1];
}
nums[j] = temp;
}
}
2.2 希尔排序
-
原理:插入排序的改进办法,通过缩小增量的插入排序来降低时间复杂度,gap开始为数组的一半,每次减半,每轮都完成一次跨越gap的插入排序。
-
时间复杂度: O ( n 1.3 ) O(n^{1.3}) O(n1.3),较难证明,可以写作 O ( n log n ) O(n\log n) O(nlogn)
-
空间复杂度:同时间复杂度
-
稳定性:由于分组的存在,不稳定
-
参考代码
public static void shellSort(int[] nums){
int gap = nums.length;
while(true){
gap /= 2;
for(int i = 0; i < gap; i++){
temp = nums[i];
for(int j = i; j > 0 && temp > nums[j]; j -= gap){
nums[j] = nums[j - gap];
}
nums[i] = temp;
}
if(gap == 1) break;
}
}
2.2 冒泡排序
-
原理:”车轮式的比武,每次决出胜者将参与下一次比武,直到选出最强者;每次选出剩余角色的最强者都需要进行一轮比武"
-
时间复杂度:由原理易知为 O ( n 2 ) O(n^2) O(n2)
-
空间复杂度:常数
-
稳定性:稳定
-
参考代码
public static void bubbleSort(int nums){
for(int i = 1; i < nums.length; i++){
boolean changed = false;
for(int j = 0; j < nums.length - i;j++){
if(nums[j] > nums[j + 1]){
swap(nums, j, j + 1);
changed = true;
}
}
if(changed == false) break;
}
}
- 双向冒泡(时间有所优化,又称“鸡尾酒排序”)
public static void bubbleSort(int nums){
int l = 0, r = nums.length - 1, shift = 1;
while(l < r){
boolean changed = false;
for(int i = l; i < r; i++){
if(nums[i] > nums[i + 1]){
swap(nums, i, i + 1);
shift = i;
}
}
r = shift;
for(int i = r - 1; i >= l; i--){
if(nums[i] > nums[i + 1]){
swap(nums, i, i + 1);
shift = i + 1;
}
}
l = shift;
}
}
2.2 计数排序
- 图示:较为简单,故无图示
- 原理:统计数字出现次数即可
- 时间复杂度:与整数范围有关
- 空间复杂度:与整数范围有关
- 稳定性:稳定
- 参考代码
public static void countingSort(int nums){
int[] counter = new int[65535];
//此处的counter数组需要随情况变化
for(int i = 0; i < nums.length; i++){
counter[nums[i]]++;
}
int idx = 0;
for(int i = 0; i < counter.length; i++){
while(counter[i] > 0)
nums[idx++] = counter[i];
}
}
- 局限性:只能排序整数;整数范围较大则开辟空间较多
3. 排序算法的应用举例
3.1 刷题需要掌握的几种算法
- 快速排序与归并排序的算法思想:分治。
分治就是把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。显然到最后,快速排序的简单拼接和归并排序的有序数组合并都属于这里所说的简单问题。 - 堆排序的核心优势–求k个最值。
前面我们说到,通过向上调整建堆时间复杂度可降低到 O ( n ) O(n) O(n),而每次向下调整堆的时间复杂度在 O ( log n ) O(\log n) O(logn)。因此,求k个最值用堆排序,即向上调整建堆,取得堆顶最值,向下调整堆,继续取堆顶最值,循环往复。如此一来,当k较小 ( < log n ) (<\log n) (<logn)时,求前k个最值时间复杂度即为建堆复杂度 O ( n ) O(n) O(n) - 已知元素范围的最佳排序–计数排序
其实在很多时候,我们待排序的数的范围已知并且最大最小值相差不大时,计数排序是最优秀的算法
3.2 leetcode排序算法题举例
- leetcode[75] 颜色分类 【中等】:
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。 - 【思路】典型的counting sort应用,由于红、白、蓝分别是0,1,2,因此待排序数组是整数,而且范围0-2很小,可以使用计数排序,而且原地排序符合要求。
class Solution {
public void sortColors(int[] nums) {
int[] counter = new int[3];
for(int i = 0; i < nums.length; i++){
counter[nums[i]]++;
}
int idx = 0;
for(int i = 0; i < 3; i++){
while(counter[i] > 0){
nums[idx++] = i;
counter[i]--;
}
}
}
}
- leetcode [1366] 通过投票对团队排名【中等】
现在有一个特殊的排名系统,依据参赛团队在投票人心中的次序进行排名,每个投票者都需要按从高到低的顺序对参与排名的所有团队进行排位。
排名规则如下:
参赛团队的排名次序依照其所获「排位第一」的票的多少决定。如果存在多个团队并列的情况,将继续考虑其「排位第二」的票的数量。以此类推,直到不再存在并列的情况。
如果在考虑完所有投票情况后仍然出现并列现象,则根据团队字母的字母顺序进行排名。
给你一个字符串数组 votes 代表全体投票者给出的排位情况,请你根据上述排名规则对所有参赛团队进行排名。
请你返回能表示按排名系统 排序后 的所有团队排名的字符串。 - 【题解】这里提供一个计数排序方法,HashMap也可解。通过统计每一个团队的投票信息进行排序,最后得到排序结果打印即可。这里相当于使用一个大小26的数组统计字符个数,是一种常用方法。
class Solution {
public String rankTeams(String[] votes) {
int len = votes[0].length();
int[][] map = new int[26][len + 1]; // 多1用于存放团队信息
for(int i = 0; i < 26; i++) map[i][len] = i;
for(int i = 0; i < votes.length; i++){
//投票统计
String s = votes[i];
for(int j = 0; j < len; j++){
map[s.charAt(j) - 'A'][j]++;
}
}
Arrays.sort(map, (a, b) ->{
//投票结果排序
for(int i = 0; i < len; i++){
if(a[i] < b[i]) return 1;
if(a[i] > b[i]) return -1;
}
return 0;
});
StringBuilder sb = new StringBuilder();
for(int i = 0; i < len; i++){
//获取结果对应团队
sb.append((char)('A' + map[i][len]));
}
return sb.toString();
}
}
- leetcode[973] 最接近原点的 K 个点(堆排序的典型应用)
- leetcode[1471] 数组中的 k 个最强值(堆排序的典型应用)
- leetcode[1481] Least Number of Unique Integers after K Removals(堆排序的典型应用)
- leetcode[179] 最大数(排序规则设计)
- leetcode [242] Valid Anagram(排序规则设计)
- leetcode [524] Longest Word in Dictionary through Deleting(排序规则设计)
- leetcode [976] Largest Perimeter Triangle(排序规则设计)
- leetcode [1451] Rearrange Words in a Sentence(排序规则设计)
- leetcode [853] Car Fleet
N 辆车沿着一条车道驶向位于 target 英里之外的共同目的地。
每辆车 i 以恒定的速度 speed[i] (英里/小时),从初始位置 position[i] (英里) 沿车道驶向目的地。
一辆车永远不会超过前面的另一辆车,但它可以追上去,并与前车以相同的速度紧接着行驶。
此时,我们会忽略这两辆车之间的距离,也就是说,它们被假定处于相同的位置。
车队 是一些由行驶在相同位置、具有相同速度的车组成的非空集合。注意,一辆车也可以是一个车队。
即便一辆车在目的地才赶上了一个车队,它们仍然会被视作是同一个车队。 - 【题解】此题也是排序规则设计,基于这样一个事实:如果某辆车起点在前面,但(如果单独行动)到达目的地的时间比起点在后面的车晚,则可以说明被超车,会被组成车队;因此计算到达花费时间,排序,然后统计车队数量即可
class Solution {
public int carFleet(int target, int[] position, int[] speed) {
int n = position.length, res = 0;
double[][] cars = new double[n][2];
//分别记录开始位置和到达时间
for(int i = 0; i < n; i++){
cars[i][0] = position[i];
cars[i][1] = (double)(target - position[i])/speed[i];
}
//开始位置排序
Arrays.sort(cars, (a, b) -> Double.compare(a[0], b[0]));
double cur = 0;
for(int i = n - 1; i >= 0 ; i--){
//能否追上前车
if(cars[i][1] > cur){
cur = cars[i][1];
res++;
}
}
return res;
}
}
4. 小结
- 基本有序时或逆序时快速排序慢;基本有序时插入、希尔、冒泡快;逆序时冒泡排序慢
- “分组错乱”的方法都不稳定
- 平均时间 O ( n log n ) O(n \log n) O(nlogn)方法优缺点要明确:快排速度最快,但可能出现较慢情况,不稳定;归并稳定且可用于外部排序,但消耗空间大;堆排序适用于排前k个,不稳定
- 计数排序很好用,若是整数且范围小,请用计数排序
- 求前k个用堆排序或选择排序
- 快排核心在于划分思想