Leetcode_动态规划
70. 爬楼梯
有n级台阶,每次有两种方法上楼(一次上一节/一次上两节)。问:有多少种方案?
https://leetcode-cn.com/problems/climbing-stairs/
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
解题思路
动态规划:
一个问题的最优解,可以从其子集的最优解组合而得。
- 第i级台阶的方法总数=(i-1)级台阶方法总数 + (i-2)级台阶方法总数
- 例外:n<=2 时,排除掉即可。
-
时间复杂度:O(n)
-
空间复杂度:O(n),需要长度为n的数组。
代码
class Solution(object):
def climbStairs(self, n):
if n == 1:
return 1
if n == 2:
return 2
first = 1
second = 2
res = 0
for i in range(2,n):
res = first + second
first = second
second = res
return res
198. 打家劫舍
链接:https://leetcode-cn.com/problems/house-robber/
有k间房,只能隔一间偷一个。问你能偷到的最大金额。
example:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
解题思路
动态规划:
- 定义子问题
- 写出子问题的递推关系
- 确定 DP 数组的计算顺序
- 空间优化(可选)
-
定义子问题:
- 有k间房,用f(k)表示k与k之前偷窃到的最高金额。
- 隔一间偷一间:如果偷了k,则不能偷k-1。
-
子问题的递推关系:
- 只有一间房时(k=1),f(1)=A(1)
- k = 2 时,对比A(1)与A(2)的最大值。f(2)=max(A(1),A(2))
- k = 3 时,对比f(3) = max(f(1)+A(3),f(2))
- 以此类推,k间房,每间房的金额为nums[0],nums[1]…nums[k-1],f(k) = max(f(k-2)+nums[k-1],f(k-1))
- 因为列表是从0开始索引,而房间号是从1开始索引,为了便于理解,在开头添加一个dp[0]=0,表示一间没偷时,金额总数为0。
-
确定顺序:
- 从下到上
代码
class Solution(object):
def rob(self, nums):
N = len(nums)
if N == 0:
return 0
dp = [0]*(N+1)
dp[0] = 0
dp[1] = nums[0]
for i in range(2,N+1):
dp[i] = max(dp[i-2]+nums[i-1],dp[i-1])
return dp[N]
因为dp[n]仅与dp[n-2]&dp[n-1]有关,可以使用old,new更新
- 空间复杂度为:O(1)
- new,old = max(old+num,new),new 这里old更新的为new的输入值而非输出值。
class Solution:
def rob(self, nums: List[int]) -> int:
old,new = 0,0
for num in nums:
new,old = max(old+num,new),new
return new
213. 打家劫舍 II
链接:https://leetcode-cn.com/problems/house-robber-ii/
有k间房,最后一间和第一间相连,只能隔一间偷一个。问你能偷到的最大金额。
解题思路
- 同198题,难点在于此题将收尾相连成为环状排列。
- 题目要求:第一个房子和最后一个房子不能一起偷。即首尾不能同时存在。
- 解决方法:拆环,将环装排列拆成两个单排,最后比较两个单排的大小。
- 偷第一个房子,列表变更为num[:-1]
- 偷最后一个房子,列表变更为num[1:]
其他同T198
- 时间复杂度:O(n)
- 空间复杂度:O(n)
代码
class Solution(object):
def rob(self, num):
if len(num) == 1:
return num[0]
def result(nums):
N = len(nums)
if N == 0:
return 0
dp = [0]*(N+1)
dp[0] = 0
dp[1] = nums[0]
for i in range(2,N+1):
dp[i] = max(dp[i-2]+nums[i-1],dp[i-1])
return dp[N]
return(max(result(num[1:]),result(num[:-1])))
因为dp[n]仅与dp[n-2]&dp[n-1]有关,可以使用old,new更新
- 空间复杂度为:O(1)
代码
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums) == 1:
return nums[0]
def result(num):
old,new = 0,0
for nums in num:
new,old = max(old+nums,new),new
return(new)
return(max(result(nums[1:]),result(nums[:-1])))
64. 最小路径和
链接:https://leetcode-cn.com/problems/minimum-path-sum/
给定非负整数的m x n网络,找到从(0,0)到(m-1,n-1)的最小路径和(从左上走到右下经过的所有数字和)
example:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
解题思路
这是一道二维的动态规划题,化二维为一维就思考每条路的走法:
- 构造一个与grid尺寸相同的dp二维列表。
- 自左上向右下,用dp[i][j]代表到达grip[i][j]的最小和,有两条路线可以到达(i,j),从左边(i-1,j)和上边(i,j-1)
- 用min()函数比较两条线路的最小即可,注意排除边界情况。
- 时间复杂度:O(mn)
- 空间复杂度:O(mn)
代码
class Solution(object):
def minPathSum(self, grid):
#利用dp构造一个新的网络用于储存
m = len(grid)
n = len(grid[0])
dp = [[0]*n for i in range(m)]
dp[0][0] = grid[0][0]
for i in range(m):
for j in range(n):
if i == j == 0:
continue
elif i == 0:
dp[0][j] = grid[0][j] + dp[0][j-1]
elif j == 0:
dp[i][0] = grid[i][0] + dp[i-1][0]
else:
dp[i][j] = grid[i][j] + min(dp[i-1][j],dp[i][j-1])
return dp[m-1][n-1]
因只与(i-1,j),(i,j-1)有关,所以可以不用构造dp,直接在原列表中更新
- 时间复杂度:O(mn)
- 空间复杂度:O(1)
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
m = len(grid)
n = len(grid[0])
for i in range(m):
for j in range(n):
if i==j==0:
continue
elif i==0:
grid[i][j] = grid[0][j-1] + grid[i][j]
elif j==0:
grid[i][j] = grid[i-1][0] + grid[i][j]
else:
grid[i][j] = min(grid[i-1][j],grid[i][j-1]) + grid[i][j]
return(grid[-1][-1])
62. 不同路径
链接:https://leetcode-cn.com/problems/unique-paths/
m * n大小的方格,从左上角走到右下角的路径总数。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-y9CqQzln-1593597823054)(attachment:image.png)]
解题思路
动态规划
题目要求总路径,那就设dp[i][j]为到达[i][j]位置的总路径数,那么dp[i][j]=dp[i-1][j]+dp[i][j-1]
- 时间复杂度:O(m*n)
- 空间复杂度:O(m*n)
代码
class Solution(object):
def uniquePaths(self, m, n):
dp = [[0]*m for _ in range(n)]
for i in range(n):
for j in range(m):
if i == 0 or j == 0:
dp[i][j] = 1
else:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return(dp[n-1][m-1])
303. 区域和检索 - 数组不可变
链接:https://leetcode-cn.com/problems/range-sum-query-immutable
给定一个整数数组nums,求出数组从索引i到j(i≤j)范围内元素的总和,包含i,j两点。
example:
给定 nums = [-2, 0, 3, -5, 2, -1],求和函数为 sumRange()
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
解题思路
动态规划 要求总和,就令dp[i]代表i和i以前的数据和。
- 计算i~j的和就是dp[j]-dp[i-1]。为了避免i-1超出范围,改为,dp[j]-dp[i]+nums[i]。
- 要调用nums和dp。需要使用self.nums&self.dp
- 时间复杂度:O(n)
- 空间复杂度:O(n)
代码
python
class NumArray(object):
def __init__(self, nums):
self.nums = nums
n = len(nums)
dp = [0]*n
sum = 0
for i in range(n):
sum += nums[i]
dp[i] = sum
self.dp = dp
def sumRange(self, i, j):
return(self.dp[j]-self.dp[i]+self.nums[i])
413. 等差数列划分
链接:https://leetcode-cn.com/problems/arithmetic-slices/
如果一个数列大于等于3个数,且两两差值相等,则称为等差数列。问一个任意数列有多少等差数列。
example:
A = [1, 2, 3, 4]
返回: 3, A 中有三个子等差数组: [1, 2, 3], [2, 3, 4] 以及自身 [1, 2, 3, 4]
解题思路
- 动态规划:题目要求所有等差数列个数,设dp[i]表示以i位置结尾的等差数列数量(官方解答其实就是这个意思)
- 那么整个数组A的等差数组个数就为sum[dp]
代码
class Solution(object):
def numberOfArithmeticSlices(self, A):
#以dp[i]表示到达i位置时的等差数列总和
n = len(A)
if n<3:
return 0
dp = [0]*n
for i in range(2,n):
if A[i-2]+A[i] == A[i-1]*2:
dp[i] = dp[i-1]+1
return sum(dp)
343. 整数拆分
链接:https://leetcode-cn.com/problems/integer-break/
将整数n拆分成多个整数,求拆分后的最大乘积。
example:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
解题思路
- 动态规划:求整数n时的最大乘积,则设dp[i]为i时的最大乘积。最后输出dp[n]
- 为什么能用动态规划?
- n=1,dp[1]=1
- n=2,dp[2]=1
- n=3,dp[3]=max(1x(3-1),2*(3-2))=max(1x(dp[2],(3-1)),2x(dp[1],(3-2)))
- n=k,dp[k]=max(1x(k-1),2x(k-2),(k-1)x(k-(k-1))))=max(1x(dp[k-1],(k-1)),2x(dp[k-2],(k-2)),(k-1)x(dp[1],1))
- 由递推可得,dp[i]=max(jdp[i-j],j(i-j),dp[i])。
- 为什么有j*(i-j)?
- 因为dp[i-j]的结果中无(i-j),只有1*(i-j-1)
代码
class Solution(object):
def integerBreak(self, n):
dp = [0]*(n+1)
dp[1] = 1
for i in range(2,n+1):
for j in range(1,i):
dp[i] = max(j*dp[i-j],j*(i-j),dp[i])
return dp[n]
279. 完全平方数
链接:https://leetcode-cn.com/problems/perfect-squares/
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。找到最小的完全平方数组合,可以重复使用。
example:
输入: n = 13
输出: 2
解释: 13 = 4 + 9
解题思路
- 动态规划:因为要求完全平方数个数最少,设i的最少完全平方数为dp[i],用j表示完全平方数。那么dp[i]=dp[i-j]+1,因此可以使用动态规划。
- 问题的关键是n是由哪几个完全平方数组成最小,比如12:可以是dp[8]+dp[4],也可以是dp[3]+dp[9],用square构建完全平方数列表,用j在里面循环输出dp[i]最小值。
代码
class Solution(object):
def numSquares(self, n):
dp = [float('inf')]*(n+1)
dp[0] = 0
square = [i**2 for i in range(int(math.sqrt(n))+1)]
for i in range(1,n+1):
for j in square:
if i < j:
break
else:
dp[i] = min(dp[i],dp[i-j]+1)
return dp[n]
300. 最长上升子序列
链接:https://leetcode-cn.com/problems/longest-increasing-subsequence/
给定一个无序的整数数组,求其中最长递增子序列的长度。可以跳序组合子序列
example:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
解题思路
- 本题难点:子序列可以跳序组合的,用dp[i]=dp[j]+1解决,具体如下:
- 时间复杂度:O(n^2),i,j两个循环
- 空间复杂度:O(n),需要长度为n的dp
- 动态规划:用dp[i]表示s[i]为结尾的最长子序列长度
- 找到[:i]中s[j]小于s[i]的最长子序列dp[j],长度+1即可。用dp[i]来缓存最长结果,直到小循环j结束。
- 最后输出整个序列中的最大值即可 max(dp[i] for i in range(n))
代码
class Solution(object):
def lengthOfLIS(self, nums):
#因要求最长递增子序列的长度,那么dp[i]就为以i结尾的最长递增序列长度
n = len(nums)
if n == 0:
return 0
dp=[1]*n
#对于s[i],因为可以跳序组合,所以需要j重新遍历s[:i+1]来找到dp[i],只要s[i]>s[j],dp[i]=dp[j]+1
for i in range(1,n):
for j in range(i):
if nums[i]>nums[j]:
dp[i] = max(dp[i],dp[j]+1)
return max(dp[i] for i in range(n))
646. 最长数对链
链接:https://leetcode-cn.com/problems/maximum-length-of-pair-chain/
列表pairs由n个数对构成。数对由两个数组成,且第一位小于第二位。对于[[a,b],[c,d]],若b example: 背包问题实际上也只是动态规划中的一类 链接:https://leetcode-cn.com/problems/longest-common-subsequence/ 两个字符串text1&text2。求最长公共子序列长度(LCS) example: 链接:https://leetcode-cn.com/problems/partition-equal-subset-sum/ 能否整分正数组 example: 动态规划 + 01背包问题 链接:https://leetcode-cn.com/problems/target-sum/ 数组nums为非负整数组,每个使用一次,通过在数前添加+/-号使结果为S,求方法数量 example: 链接:https://leetcode-cn.com/problems/ones-and-zeroes/ 有m个0,n个1,和k个字符串,求最多能拼出多少个字符串。 example: 两个背包,0背包和1背包,字符串会占用两个背包的空间,受益是1。 链接:https://leetcode-cn.com/problems/coin-change/ 多种面额硬币coins,每种不限数量,组成总金额amount。求所需最小硬币数。 example: 求用coins使用数量最小值,那就设dp[i][j]代表使用[0,i]个币种组成j的最小数量。 dp[i][j]=min(dp[i-1][j],1+dp[i-1][j-coins[i],1+dp[i][j-coins[i]]]) 对于2.2,2.3如果对coins从小到大排序,则j-coins[i]只会出现在i处,即: dp[i][j]=min(dp[i-1][j],1+dp[i][j-coins[i]]) dp[j]=min(dp[j],1+dp[j-coins]) 链接:https://leetcode-cn.com/problems/coin-change-2 不同面额钱币coins,组成金额amount的组合数有多少 example: 动态规划,同T322,采用顺序优化方法降维。 链接:https://leetcode-cn.com/problems/word-break/ 非空字符串s是否可以被空格拆分成字典wordDict中的值。 example: 链接:https://leetcode-cn.com/problems/combination-sum-iv/ nums为不重复的正整数数组,target为目标和,nums有多少种组合方式(不同排序算作不同组合) example: 股票交易共六种题型,设dp[i][k][0 or 1]表示第i天股票是持有(用1表示),还是不持有(用0表示),第i天还有k次交易次数 状态转移方程: 链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/ 股票每天有买入buy,卖出sell,不操作rest三种操作,求第i天最大利润。(卖出后需要间隔一天才能买入,冷冻期) example: 链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee 股票每天有买入buy,卖出sell,不操作rest三种操作,求第i天最大利润。在卖出时收取一次手续费fee,卖出后才可买入。 example: 链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii/ 股票每天有买入buy,卖出sell,不操作rest三种操作,求第i天最大利润。最多完成两笔交易,(买入卖出一起算一笔) example: 链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iv/ 股票每天有买入buy,卖出sell,不操作rest三种操作,求第i天最大利润。最多完成k笔交易,(买入卖出一起算一笔) example: 链接:https://leetcode-cn.com/problems/delete-operation-for-two-strings/ 给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。 example 链接:https://leetcode-cn.com/problems/edit-distance/ 两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 。操作有:删除,替换,增加。 链接:https://leetcode-cn.com/problems/2-keys-keyboard/ 最开始只有一个字符 A,问需要多少次操作能够得到 n 个字符 A,每次操作可以复制当前所有的字符,或者粘贴。 example: 链接:https://leetcode-cn.com/problems/count-submatrices-with-all-ones/ 给你一个只包含 0 和 1 的 rows * columns 矩阵 mat ,请你返回有多少个 子矩形 的元素全部都是 1 example: 前言:做这题思路一直绕在了动态规划里面,想着dp[i][j]表示到mat[i][j]时的最多子矩形个数。结果推出了状态转移方程为: 思路转变:如果将每个mat[i][j]为右下顶点的矩形个数进行求和,在mat[-1][-1]时,即可输出结果。(反正tmp这个东西必求,何必再用个dp) 求以mat[i][j]为右下顶点的子矩形个数难点解答,代码中相应注释: 时间复杂度:算不清,空间复杂度:O(n*m) 这个解答汇总很棒输入: [[1,2], [2,3], [3,4]]
输出: 2
解释: 最长的数对链是 [1,2],[3,4]
解题思路
代码
class Solution(object):
def findLongestChain(self, pairs):
n = len(pairs)
dp = [1]*n
#先将数对以0位进行排序
pairs.sort(key=lambda x:x[0])
#dp[i]表示第i对的最长数对链
for i in range(1,n):
for j in range(i):
if pairs[i][0]>pairs[j][1]:
dp[i]=max(dp[i],dp[j]+1)
return max(dp[i] for i in range(n))
背包问题
1143. 最长公共子序列
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace",它的长度为 3。
解题思路
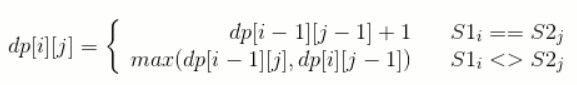
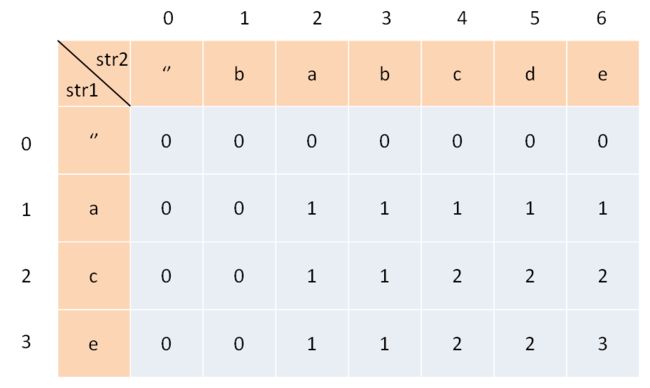
代码
class Solution(object):
def longestCommonSubsequence(self, text1, text2):
n,m = len(text1),len(text2)
dp = [[0]*(m+1) for _ in range(n+1)]
for i in range(1,n+1):
for j in range(1,m+1):
if text1[i-1]==text2[j-1]:
dp[i][j]=dp[i-1][j-1]+1
else:
dp[i][j]=max(dp[i-1][j],dp[i][j-1])
return(dp[n][m])
416. 分割等和子集
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11]
解题思路
代码
class Solution(object):
def canPartition(self, nums):
sums,n = sum(nums),len(nums)
if sums % 2 == 1:
return False
target = sums/2
dp = [[False]*(target+1) for _ in range(n)]
nums.sort()
for i in range(n):
for j in range(nums[i],target+1):
if nums[i]==j:
dp[i][j]=True
else:
dp[i][j]=dp[i-1][j] or dp[i-1][j-nums[i]]
return dp[-1][-1]
494.目标和
输入: nums: [1, 1, 1, 1, 1], S: 3
输出: 5
解释:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。
解题思路
代码
class Solution(object):
def findTargetSumWays(self, nums, S):
n = len(nums)
sums = sum(nums)
if sums<S:
return 0
dp = [[0]*(2*sums+1) for _ in range(n)]
#第一行初始化,需要注意的是+,-有可能指向同一个数,所以使用叠加+=1而不是赋值=1
dp[0][sums-nums[0]]+=1
dp[0][sums+nums[0]]+=1
for i in range(1,n):
for j in range(2*sums+1):
l = dp[i-1][j-nums[i]] if 0<=j-nums[i]<(2*sums+1) else 0
r = dp[i-1][j+nums[i]] if 0<=j+nums[i]<(2*sums+1) else 0
dp[i][j] = l + r
return dp[n-1][sums+S]
474.一和零
输入: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3
输出: 4
解释: 总共 4 个字符串可以通过 5 个 0 和 3 个 1 拼出,即 "10","0001","1","0" 。
解题思路
dp[i][j]=max(dp[i][j],1+dp[i-count_0][j-count_1])
代码
class Solution(object):
def findMaxForm(self, strs, m, n):
dp=[[0]*(n+1) for _ in range(m+1)]
for item in strs:
count_0 = item.count("0")
count_1 = item.count("1")
for i in range(m,count_0 -1,-1):
for j in range(n,count_1 -1,-1):
dp[i][j] = max(dp[i][j],1+dp[i-count_0][j-count_1])
return dp[m][n]
322.零钱兑换
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
解题思路
1. 动态规划:

2. 状态转移方程:
3. 优化:
4. 时间复杂度:O(N*amount),N为coins种类
5. 空间复杂度:O(amount)
代码
class Solution(object):
def coinChange(self, coins, amount):
n = len(coins)
coins.sort()
dp=[float("inf")]*(amount+1)
dp[0]=0
for cost in coins:
for j in range(cost,amount+1):
dp[j]=min(dp[j],dp[j-cost]+1)
return dp[amount] if dp[amount]!=float("inf") else -1
518.零钱兑换二
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
解题思路

在(0,coins[i]),dp[i,j]=dp[i-1][j];在(coins[i],amount+1),dp[i][j]=dp[i-1][j]+dp[i][j-coins[i]]。
dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]
代码
class Solution(object):
def change(self, amount, coins):
dp = [0]*(amount+1)
dp[0] = 1
for cost in coins:
for j in range(cost,amount+1):
dp[j] = dp[j] + dp[j-cost]
return dp[amount]
139.单词拆分
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
解题思路
代码
class Solution(object):
def wordBreak(self, s, wordDict):
n=len(s)
dp=[False]*(n+1)
dp[0]=True
for i in range(n):
for j in range(i+1,n+1):
if dp[i] and (s[i:j] in wordDict):
dp[j]=True
return dp[-1]
377. 组合总和 Ⅳ
nums = [1, 2, 3]
target = 4
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。
解题思路
如4=2+2的组合中,虽然是2对已有排序dp[2]的插空:
{1,1,2},{1,2,1},{2,1,1},{2,2}
但实际上:
{1,2,1},{2,1,1}属于dp[3]类。代码
class Solution(object):
def combinationSum4(self, nums, target):
dp = [0]*(target+1)
dp[0]=1
for i in range(1,target+1):
for j in nums:
if i>=j:
dp[i] += dp[i-j]
return dp[target]
股票交易问题
初始化:
309. 最佳买卖股票时机(含冷冻期)
输入: [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
解题思路
代码
class Solution(object):
def maxProfit(self, prices):
n = len(prices)
if n<2:
return 0
dp = [[0]*2 for _ in range(n+1)]
dp[0][0] = dp[1][0] = 0
dp[0][1] = dp[1][1] = -prices[0]
for i in range(2,n+1):
dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i-1])
dp[i][1]=max(dp[i-1][1],dp[i-2][0]-prices[i-1])
return dp[n][0]
714.买卖股票的最佳时机(含手续费)
输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
解释: 能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
解题思路
代码
class Solution(object):
def maxProfit(self, prices, fee):
n = len(prices)
dp = [[0]*2 for _ in range(n+1)]
dp[0][0],dp[0][1]=0,float('-inf')
for i in range(1,n+1):
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i-1]-fee)
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i-1])
return dp[n][0]
代码
class Solution(object):
def maxProfit(self, prices, fee):
n = len(prices)
dp = [0,float('-inf')]
for i in range(1,n+1):
dp[0] = max(dp[0],dp[1]+prices[i-1]-fee)
dp[1] = max(dp[1],dp[0]-prices[i-1])
return dp[0]
123.买卖股票的最佳时机三(最多完成k=2笔交易)
输入: [3,3,5,0,0,3,1,4]
输出: 6
解释: 在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
解题思路
代码
class Solution(object):
def maxProfit(self, prices):
n = len(prices)
if n<1:
return 0
dp = [[[0]*2 for _ in range(3)] for _ in range(n+1)]
for k in range(3):
dp[0][k][1] = float('-inf')
for i in range(1,n+1):
for k in range(1,3):
dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1]+prices[i-1])
dp[i][k][1] = max(dp[i-1][k][1],dp[i-1][k-1][0]-prices[i-1])
return dp[n][2][0]
6. 卖出时算做交易
for i in range(1,n+1):
for k in range(3):
dp[i][0][0] = 0
dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k-1][1]+prices[i-1])
dp[i][k][1] = max(dp[i-1][k][1],dp[i-1][k][0]-prices[i-1])
return dp[n][2][0]
7. 优化
* dp[i]仅与dp[i-1]有关,可降维
* dp[k][0] = max(dp[k][0],dp[k][1]+prices[i-1])
* dp[k][1] = max(dp[k][1],dp[k-1][0]-prices[i-1])
* 时间复杂度:O(2n),空间复杂度:O(1),只需要6的常数空间。
代码
class Solution(object):
def maxProfit(self, prices):
n = len(prices)
dp = [[0]*2 for _ in range(3)]
for k in range(3):
dp[k][1] = float('-inf')
for i in range(1,n+1):
for k in range(1,3):
dp[k][0] = max(dp[k][0],dp[k][1]+prices[i-1])
dp[k][1] = max(dp[k][1],dp[k-1][0]-prices[i-1])
return dp[2][0]
188.买卖股票的最佳时机 IV(指定k)
输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
解题思路
本题还存在k=infinite无穷的情况,同T714,因为一笔交易包含一买一卖两天操作,所以k<=n/2;当k>=n/2时,可看做k=float(‘inf’) dp[i][k1][0] = max(dp[i-1][k1][0],dp[i-1][k1][1]+prices[i-1])
dp[i][k1][1] = max(dp[i-1][k1][1],dp[i-1][k1-1][0]-prices[i-1])
dp[0][k][1]=float(’-inf’) ,第0天,不论k取和值,都不存在持有的情况代码
class Solution(object):
def maxProfit(self, k, prices):
n = len(prices)
#k>2/n时,相当于k=float('inf')
def maxProfit_infk(prices):
dp = [[0]*2 for _ in range(n+1)]
dp[0][1]=float('-inf')
for i in range(1,n+1):
dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i-1])
dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i-1])
return dp[n][0]
if k>n/2:
return maxProfit_infk(prices)
dp = [[[0]*2 for _ in range(k+1)] for _ in range(n+1)]
for k1 in range(k+1):
dp[0][k1][1] = float('-inf')
for i in range(1,n+1):
for k1 in range(1,k+1):
dp[i][k1][0] = max(dp[i-1][k1][0],dp[i-1][k1][1]+prices[i-1])
dp[i][k1][1] = max(dp[i-1][k1][1],dp[i-1][k1-1][0]-prices[i-1])
return dp[n][k][0]
6.优化
* dp[i]仅与dp[i-1]有关,3维降2维
* dp[k1][0] = max(dp[k1][0],dp[k1][1]+prices[i-1])
* dp[k1][1] = max(dp[k1][1],dp[k1-1][0]-prices[i-1])
* 时间复杂度:O(nk),空间复杂度(2k)
代码
class Solution:
def maxProfit(self, k, prices):
n = len(prices)
def maxProfit_infk(prices):
dp = [0]*2
dp[1]=float('-inf')
for i in range(1,n+1):
dp[0]=max(dp[0],dp[1]+prices[i-1])
dp[1]=max(dp[1],dp[0]-prices[i-1])
return dp[0]
if k>n/2:
return maxProfit_infk(prices)
dp = [[0]*2 for _ in range(k+1)]
for k1 in range(k+1):
dp[k1][1] = float('-inf')
for i in range(1,n+1):
for k1 in range(1,k+1):
dp[k1][0] = max(dp[k1][0],dp[k1][1]+prices[i-1])
dp[k1][1] = max(dp[k1][1],dp[k1-1][0]-prices[i-1])
return dp[k][0]
583. 两个字符串的删除操作
输入: "sea", "eat"
输出: 2
解释: 第一步将"sea"变为"ea",第二步将"eat"变为"ea"
解题思路
代码
class Solution(object):
def minDistance(self, word1, word2):
n,m = len(word1),len(word2)
dp = [[0]*(m+1) for _ in range(n+1)]
for i in range(n+1):
for j in range(m+1):
if i==0 or j==0:
dp[i][j]=i+j
elif word1[i-1]==word2[j-1]:
dp[i][j]=dp[i-1][j-1]
else:
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+1
return dp[n][m]
72. 编辑距离
解题思路
代码
class Solution(object):
def minDistance(self, word1, word2):
n,m = len(word1),len(word2)
dp = [[0]*(m+1) for _ in range(n+1)]
for i in range(n+1):
for j in range(m+1):
if i==0 or j==0:
dp[i][j]=i+j
elif word1[i-1]==word2[j-1]:
dp[i][j]=dp[i-1][j-1]
else:
dp[i][j]=min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1
return(dp[n][m])
650. 只有两个键的键盘
输入: 3
输出: 3
解释:
最初, 我们只有一个字符 'A'。
第 1 步, 我们使用 Copy All 操作。
第 2 步, 我们使用 Paste 操作来获得 'AA'。
第 3 步, 我们使用 Paste 操作来获得 'AAA'
解题思路
代码
class Solution(object):
def minSteps(self, n):
dp=[0]*(n+1)
for i in range(2,n+1):
minCount=i
for j in range(1,i):
if i % j == 0:
minCount = min(dp[j] + i/j , minCount)
dp[i]=minCount
return dp[n]
5454. 统计全 1 子矩形_第196场周赛第3题
输入:mat = [[1,0,1],
[1,1,0],
[1,1,0]]
输出:13
解释:
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。
解题思路
dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]+tmp
如何求得以mat[i][j]为右下顶点的子矩形个数代码
class Solution(object):
def numSubmat(self, mat):
n,m = len(mat),len(mat[0])
ans = 0 #保存子矩形个数
for i in range(n):
for j in range(m):
if mat[i][j]==1:
left,top = -1,-1
y = i
while y > top: #从mat[i][j]向0行迭代
x = j
while x > left: #从mat[i][j]向0列迭代
if mat[y][x]==0:
left = x #更新左边界
else:
ans += 1
x -= 1
y -= 1
return ans

