哈夫曼树/编码：java实现
哈夫曼树
给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树。通俗一点说就是出现次数越多的，即权重最大的，到根节点最短。可以应用在编码，压缩上面。
哈夫曼编码
构建哈夫曼编码需要进行以下五步操作
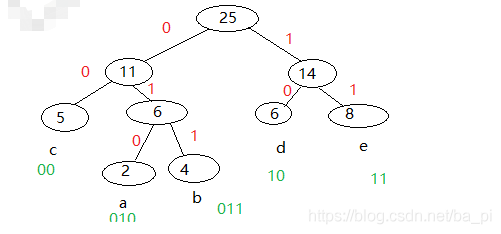
- 构建一个哈夫曼队列，队列里面的内容是所有出现字符以及组合的权重大小（s1,s2,s3及s4,指权重之和），由小到大排列。例如：a×2 ,b×4，c×5，d×6，e×8。最后构建的队列顺序如下图
代码如下
private static List<HfQueueNode> getHfQueue(String string) {
List<HfQueueNode> hfQueueNodes = new LinkedList<>();
/**
* 编码字符加入map
*/
char[] chars = string.toCharArray();
Map<String, Integer> charCountMap = new LinkedHashMap<>();
for (char aChar : chars) {
Integer charCount = charCountMap.get(String.valueOf(aChar));
if (charCount == null) {
charCountMap.put(String.valueOf(aChar), 1);
} else {
charCountMap.put(String.valueOf(aChar), ++charCount);
}
}
// 队列列表
/**
* 遍历Map加入队列
*/
List<HfQueueNode> hfTreeNodes = new LinkedList<>();
charCountMap.forEach((k, v) -> {
HfQueueNode hfQueueNode = new HfQueueNode();
hfQueueNode.setData(k);
hfQueueNode.setCount(v);
hfQueueNode.setIsData(true);
hfTreeNodes.add(hfQueueNode);
});
/**
* 顺序由次数 高到低排列
*/
List<HfQueueNode> collect = hfTreeNodes.stream().sorted(Comparator.comparingInt(HfQueueNode::getCount).reversed()).collect(Collectors.toList());
addHfQueueNode(collect, hfQueueNodes);
return hfQueueNodes;
}
/**
* 添加队列
*
* @param hfQueueNodes
* @return
*/
public static List<HfQueueNode> addHfQueueNode(List<HfQueueNode> hfQueueNodes, List<HfQueueNode> finalQueue) {
if (hfQueueNodes.size() == 1) {
HfQueueNode rootNode = new HfQueueNode();
rootNode.setIsData(false);
rootNode.setData(String.valueOf(hfQueueNodes.get(0).getCount() + hfQueueNodes.get(0).getCount()));
rootNode.setCount(hfQueueNodes.get(0).getCount() + hfQueueNodes.get(0).getCount());
finalQueue.addAll(hfQueueNodes);
// finalQueue.add(rootNode);
return finalQueue;
} else {
HfQueueNode latestFirstNode = hfQueueNodes.remove(hfQueueNodes.size() - 1);
HfQueueNode latestSecondNode = hfQueueNodes.remove(hfQueueNodes.size() - 1);
finalQueue.add(latestFirstNode);
finalQueue.add(latestSecondNode);
HfQueueNode sumNode = new HfQueueNode();
sumNode.setIsData(false);
int count = latestFirstNode.getCount() + latestSecondNode.getCount();
sumNode.setCount(count);
/**
* 以最新的次数记录为数据
*/
sumNode.setData(String.valueOf(count));
hfQueueNodes.add(sumNode);
// 重新排序
List<HfQueueNode> sortQueueNodes = hfQueueNodes.stream().sorted(Comparator.comparingInt(HfQueueNode::getCount).reversed()).collect(Collectors.toList());
addHfQueueNode(sortQueueNodes, finalQueue);
return finalQueue;
}
}
- 根据哈夫曼队列构建哈夫曼树
如图
思考思路如下：
首先将所有节点分层，每一层按照从小到大顺序排列
然后将最后一层树节点挂在倒数第二层，依次递推，直到只剩顶层树节点
最后返回顶层节点
代码如下
private static HfTreeNode getHfTree(List<HfQueueNode> hfQueue) {
HfQueueNode remove = hfQueue.remove(hfQueue.size() - 1);
List<List<HfQueueNode>> lists = new ArrayList<>();
LinkedList<HfQueueNode> hfQueueNodes = new LinkedList<>();
hfQueueNodes.add(remove);
lists.add(hfQueueNodes);
List<List<HfQueueNode>> hfQueueLists = getHfQueueLists(hfQueue, lists);
List<List<HfTreeNode>> treeLists = new ArrayList<>();
hfQueueLists.stream().forEach(item1 -> {
LinkedList<HfTreeNode> hfTreeNodes = new LinkedList<>();
item1.forEach(item2 -> {
HfTreeNode hfTreeNode = new HfTreeNode();
hfTreeNode.setData(item2.getData());
hfTreeNode.setData(item2.isData());
hfTreeNode.setCount(item2.getCount());
hfTreeNodes.add(hfTreeNode);
});
treeLists.add(hfTreeNodes);
});
List<HfTreeNode> trrNode = createTreeNode(treeLists.remove(treeLists.size() - 1), treeLists.remove(treeLists.size() - 1), treeLists);
return trrNode.get(0);
}
/**
* 创建树节点node
* @param lastFirst
* @param lastSecond
* @param treeLists
* @return
*/
private static List<HfTreeNode> createTreeNode(List<HfTreeNode> lastFirst, List<HfTreeNode> lastSecond, List<List<HfTreeNode>> treeLists) {
lastSecond.forEach(item1 -> {
if (!item1.isData()) {
HfTreeNode rightNode = lastFirst.remove(0);
HfTreeNode leftNode = lastFirst.remove(0);
item1.setLeftNode(leftNode);
item1.setRightNode(rightNode);
}
});
if (treeLists.size() >= 1) {
return createTreeNode(lastSecond, treeLists.remove(treeLists.size() - 1), treeLists);
} else {
return lastSecond;
}
}
- 获取哈夫曼编码对应表，如下图
/**
* 获取哈夫曼编码，具有左子树，节编码+0，右子树节点编码+1
* @param hfTree
* @param sb
*/
private static void getHfCode(HfTreeNode hfTree, StringBuffer sb) {
if (hfTree == null) {
return;
} else {
StringBuffer leftNode = new StringBuffer();
getHfCode(hfTree.getLeftNode(), leftNode.append(sb).append(0));
if (hfTree.isData()) {
hfTableMap.put(hfTree.getData(), sb.toString());
}
StringBuffer rightNode = new StringBuffer();
getHfCode(hfTree.getRightNode(), rightNode.append(sb).append(1));
}
}
- 编码，根据哈夫曼编码表进行编码，如3，c (00),a(010)，将字符串aabbbbcccccddddddeeeeeeee编码最后结果为010 010 011 011 011 011 00 00 00 00 00 10 10 10 10 10 10 11 11 11 11 11 11 11 11
代码如下
/**
* 编码
*
* @param hfTableMap
* @param string
* @return
*/
private static String encode(Map<String, String> hfTableMap, String string) {
StringBuffer code = new StringBuffer();
for (char c : string.toCharArray()) {
code.append(hfTableMap.get(String.valueOf(c)));
}
return code.toString();
}
- 解码，输入01001001101101101100000000001010101010101111111111111111，输出aabbbbcccccddddddeeeeeeee，
代码如下
/**
* 解码
*
* @param hfTree
* @param chars
* @return
*/
private static void decode(HfTreeNode hfTree, char[] chars, int index) {
/**
* 当前是子节点，包含数据
*/
if (hfTree.isData()) {
System.out.print(hfTree.getData());
/**
* 解码完成
*/
if (index == chars.length){
return;
}else {
/**
* 继续解码，从根节点开始遍历
*/
decode(hfTreeStatic, chars, index);
}
}else {
/**
* 指针后移，依据编码是0或者1决定解子节点或者右节点
*/
index++;
if (chars[index] == '0'){
decode(hfTree.getLeftNode(),chars,index);
}else {
decode(hfTree.getRightNode(),chars,index);
}
}
}
最后验证吻合
说一点小感慨，在实现哈夫曼树的过程中，递归算法的调用倒是是用的滚瓜烂熟。
附上代码库地址:
https://gitee.com/zhoujie1/data-structure-and-algorithm.git