数值积分疯狂翻车:scipy的odeint()数值积分错误
懂的老哥还请不吝赐教
前言
本来是有学校的正版MATLAB授权的,但是特殊时期无法回校,校外下载极慢,垃圾度盘就不用指望了。于是下载了不足100MB的1999年的MATLAB(5.3.0, R11),启动之类的确实快得压啤,但是过于精简导致体验不太行(没debug,编辑器里不能直接运行脚本,说实话影响不大)。于是转入Python的numpy,scipy,matplotlib三大件,开始了新一轮的折腾。
问题
对于同一个(特定的)被积函数(相对差别:1e-8),scipy.integrate中的odeint()和MATLAB积分出来的结果差了3个数量级。而scipy.integrate中的quad()函数就和MATLAB结果一致。
这个被积函数确实有些特别,它的值和系统当前的状态没有关系,而且变化比较快速, 100 k H z ± 1 k H z 100\mathrm{kHz}\pm1\mathrm{kHz} 100kHz±1kHz能变化两三个数量级 :
def noisePSD(freq, noise_power, Cp, tao1, tao2):
"""计算噪声PSD"""
e_n, i_n = 20e-9, 40e-15
Ceq = 2*(1.15e-12 + Cp)
L, r = 5e-3, 31.415926
Rf, Cf = 1e7, 3.3e-12
lp_freq = abs(freq - 1e5)
s = freq*1j*2*np.pi
s_2 = -(freq*2*np.pi)**2
my_Z_BR = (L*s + r)/(L*Ceq*s_2 + r*Ceq*s + 1)
Z_f = Rf/(Rf*Cf*s + 1)
# 热噪声
thermal_noise_BR = 0.1287*((my_Z_BR.real)**0.5)*1e-9# 桥路热电阻V/Hz^0.5
thermal_noise_gain = -2*Z_f/my_Z_BR
th_BR_Uo = thermal_noise_BR * abs(thermal_noise_gain )
# 等效输入电压噪声
noise_gain = 1 - thermal_noise_gain
en_Uo = e_n * abs(noise_gain )
# 等效输入电流噪声
e_in_Uo = abs(Z_f )*i_n
# 反馈阻抗热噪声
th_Zf_Uo = 0.1287*((Z_f .real)**0.5)*1e-9
# 总噪声
before_psd = th_BR_Uo**2 + 2*(en_Uo**2 + e_in_Uo**2 + th_Zf_Uo**2)
# (70Hz, 350HZ)滤波器作用
temp = tao1*tao2
lp_filter = temp/(-lp_freq**2 + (tao1 + tao2)*lp_freq*1j + temp)
psd = before_psd * ((lp_filter.real)**2 + (lp_filter.imag)**2)
return psdMATLAB写了同样功能的脚本,计算了在3个 C p C_p Cp取值下, ( 1 0 5 − 750 ) : 50 : ( 1 0 5 + 750 ) H z (10^5-750):50:(10^5+750)\mathrm{Hz} (105−750):50:(105+750)Hz处的PSD,结果保存在psd.mat文件里。和Matlab结果的比较:
tao1, tao2 = (70, 350)
Cp = 252.15e-12
matlab_data = scio.loadmat('./psd.mat')
delta_Cps = matlab_data['delta_Cps']
Freq_span = matlab_data['Freq_span']
Freq_span.shape = Freq_span.size,
matlab_psds = matlab_data['PSD'].T
# compare integrands from MATLAB and Python
psds = np.empty( (delta_Cps.size, Freq_span.size), dtype=np.float64)
index = 0
for delta_Cp in delta_Cps.flat:
psds[index,:] = noisePSD(Freq_span, 0, \
(delta_Cp+1)*Cp, tao1, tao2)
index += 1
fig,axes = plt.subplots(1, 2, figsize=(18/2.54, 9/2.54), dpi=141.21)
for index in range(0,3):
axes[0].plot(Freq_span, psds[index, :], label=str(delta_Cps[0, index]))
axes[1].plot(Freq_span, (psds[index, :]-matlab_psds[index,:])/\
matlab_psds[index, :], label=str(delta_Cps[0, index]))
axes[1].legend(fontsize=10)
axes[1].xaxis.set_tick_params(labelsize=10)
axes[1].set_xlabel('frequency/Hz', fontsize=10)
axes[1].grid()
axes[0].legend(fontsize=10)
axes[0].xaxis.set_tick_params(labelsize=10)
axes[0].set_xlabel('frequency/Hz', fontsize=10)
axes[0].grid()
plt.show()下图左边是noisePSD()在各频点的值,右边是相对MATLAB结果的误差。从下图可以看到这个函数和MATLAB的被积函数是等价的。 
下面用odeint(),quad(),梯形法和solver_ivp()分别进行积分并画图:
delta_Cps = np.arange(-1e-2, 1e-2+1e-4, 1e-4)
frequency = np.linspace(1e5-500, 1e5+500, 11)
df = frequency[1] - frequency[0]# freq 线性递增
noise_powers = np.empty((4, delta_Cps.size), dtype=np.float64)
index = 0
for delta_Cp in delta_Cps:
# 使用odeint()
noise_power = odeint(noisePSD, [0], frequency,\
args=((delta_Cp+1)*Cp, tao1, tao2), tfirst=True)
noise_powers[0, index] = noise_power[-1]
# 使用quad()
noise_power = quad(noisePSD, 1e5-500, 1e5+500,\
args=(0, (delta_Cp+1)*Cp, tao1, tao2))# args是位置参数
noise_powers[1, index] = noise_power[0]
# 使用梯形法
noise_psd = noisePSD(frequency, 0, (delta_Cp+1)*252.15e-12,\
tao1, tao2)
noise_power = 0.5*df*(noise_psd[:-1] + noise_psd[1:])
noise_powers[2, index] = noise_power.sum()
# 使用solver_ivp()
result = solve_ivp(noisePSD, [1e5-500,1e5+500],np.array([0]), \
method='RK23', t_eval=frequency, args=((delta_Cp+1)*Cp, tao1, tao2), \
max_step=df)
noise_powers[3, index] = result.y[0, -1]
index += 1
fig, axes = plt.subplots(1, 2, sharex=True, figsize=(20/2.54, 10/2.54))
axes[1].plot(delta_Cps, noise_powers[0, :], label='odeint')
axes[1].legend(fontsize=10)
axes[1].set_xlabel(r'$\Delta Cp$', fontsize=10)
axes[1].xaxis.set_tick_params(labelsize=10)
axes[1].grid()
axes[0].plot(delta_Cps, noise_powers[1, :], label='quad')
axes[0].plot(delta_Cps, noise_powers[2, :], label='trapezoidal')
axes[0].plot(delta_Cps, noise_powers[3, :], label='solver_ivp')
axes[0].set_ylabel('noise power', fontsize=10)
axes[0].set_xlabel(r'$\Delta Cp$', fontsize=10)
axes[0].legend(fontsize=10)
axes[0].grid()
plt.show()积分结果比较
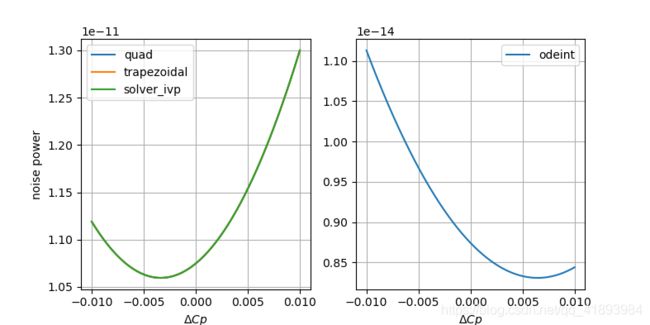
神奇的事情发生了,积分结果居然能差这么多?!在被积函数里打了断点,从单步运行中可以发现:odeint()传入的频率很奇怪。我要求的那几个频率点离传入参数十万八千里呢,这个积分真的魔幻啊。而且solver_ivp()也不是善茬,非得指定max_step=df才能好使,否则积分结果还是会上浮0.1左右,对上下文中的被积函数来说,精度比不上梯形法,速度似乎还挺慢。
体会
scipy.integrate的逻辑确实和MATLAB有很大差异(只是猜测)。举例来说,对于形如 d y d t = a ∗ y + b ∗ r ( t ) \frac{dy}{dt}=a*y+b*r(t) dtdy=a∗y+b∗r(t)的微分方程,前者区别对待了 a = 0 a=0 a=0和 a ≠ 0 a\neq0 a=0的情况(区别在于是否用到系统的状态), a = 0 a=0 a=0时使用 q u a d ( b ∗ r ( t ) , t 0 , t 1 , a r g s ) \mathrm{quad}(b*r(t),t_0,t_1,args) quad(b∗r(t),t0,t1,args)这样的函数计算 y = ∫ t 0 t 1 b ∗ r ( t ) d t y=\int_{t_0}^{t_1}b*r(t)dt y=∫t0t1b∗r(t)dt, a ≠ 0 a\neq0 a=0时使用 o d e i n t ( d y d t , y 0 , t l i s t , a r g s ) \mathrm{odeint}(\frac{dy}{dt},y_0,t_{list},args) odeint(dtdy,y0,tlist,args)来计算 y y y在各个时刻的值。MATLAB直接使用ode23()等函数,不论 a a a的取值如何。
修正:scipy.integrate在有些情况下又能积分没有用到系统状态的情况(上述的 a = 0 a=0 a=0情况)了。。。比如:
def df_dt(f, t, a):
return [a, f[0]]
def diff(f, t, a):
return [a*t]这两个函数都可以描述这样一种情形:加速度为 a a a的直线匀加速运动,区别在于df_dt()在用odeint()等积分时可以指定初速度 v 0 v_0 v0和初始位置 x 0 x_0 x0,而diff()只能指定初始位置,固定了初速度只能为 a ∗ t 0 a*t_0 a∗t0。当我们认为 [ v 0 , x 0 ] ′ = [ 0 , 0 ] ′ [v_0, x_0]'=[0,0]' [v0,x0]′=[0,0]′,并使初始时刻 t 0 = 0 t_0=0 t0=0时,这两个函数描述的系统是完全一样的,重要的是:df_dt()是用到系统状态的,diff()是没有用到状态的。而这两个被积函数被odeint()函数积分后结果是一样的,所以我上面关于是否用到系统状态的推测就是错的了。这就让答案更加扑朔迷离
总的来说,MATLAB函数使用默认参数时,适应性比较强,scipy.integrate的odeint()可能需要编程的人心里更加清楚想要的结果是什么。
目前还没明白到底是什么区别。。也许应该需要改一下odeint()默认的几个参数,比如最大步长等,也许还可以使用其他数值积分函数。
懂的老哥还请不吝赐教。