线性回归

线性模型定义

设给定一组属性x，$x=(x_1，x_2，...，x_n)$，则线性模型一般表达式：
$$y=w_1{x}_1+w_2{x}_2+w_3{x}_3+w_n{x}_n+b$$
向量形式：
$$y=w^{T}x+b$$
其中：$w=(w_1,w_2,w_3,...,w_n{)}^T，x=(x_1,x_2,x_3,...,x_4)$，经过学习，即可确定线性方程参数：w, b
线性模型实现相对较为简单，然而线性模型代表着机器学习中一些非常重要的思想。很多非线性模型可以在线性模型基础上引入层级结构(比如神经网络，若删除激活层，则进行的就是线性计算)或者经过高维映射(比如引入核函数处理维度灾难)得到。线性模型具有很好的解释性，比如引用西瓜书的知识判断一个西瓜是否是好瓜，可以用：
$$f_{好瓜}(x)=0.2x_{色泽}+0.5x_{根蒂}+0.3x_{敲声}+1$$
此公式表示：一个西瓜可以通过色泽，根蒂，敲声等特征共同判断好坏，并且权重越大，表示该特征更具有代表性。

损失函数

采用均方差损失函数
$$E=\frac{1}{2}\sum _{i=1}^n(y-y^{\prime }{)}^2$$
线性回归任务就是试图找到一组参数使得损失函数最小

最小二乘法：

此方法直接使用损失函数对w和b求导，分别令导函数为0即可得到最优解。

• 实际存在的问题
  1）最小二乘法需要求解逆矩阵，但有可能逆矩阵根本不存在；
  2）当样本特征数量较多时，计算逆矩阵耗时甚至不可行

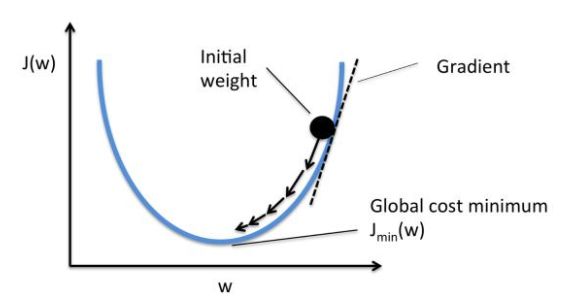
梯度下降法

• 梯度是一个向量(矢量)，表示某一函数在一点处的方向导数沿着此向量代表的方向取得最大值，即函数在该点沿着该方向变化最快，损失函数沿着梯度相反方向收敛最快。当梯度向量为零或者接近零时，说明已经找到一个极值点，从而将损失值收敛到某个极小值。

• 执行过程
  1）损失值是否小于设定值？是则结束梯度下降过程，否则计算损失函数在该点的梯度；
  2）待优化参数向着梯度反方向变化一定的值以试图减小损失
  3）循环到1）
  

• 参数更新法则
  将令$b=w_0,w_1=w^T$，直线方程有两个参数需要学习，$w_0$和$w_1$，梯度下降中，分别对两个参数单独优化，调整法则如下：
  $$w_0=w_0+\Delta w_0$$
  $$w_1=w_1+\Delta w_1$$
  $\Delta w_0和\Delta w_1$ 可以表示为：
  $$\Delta w_0=-\eta \frac{\Delta loss}{\Delta w_0}$$
  $$\Delta w_1=-\eta \frac{\Delta loss}{\Delta w_1}$$
  其中，$\eta$称为学习率，$\frac{\Delta loss}{\Delta w_i}$为梯度
  损失函数表达式：
  $$loss=\frac{1}{2}\sum _{i=1}^n(y-y^{\prime }{)}^2=\frac{1}{2}\sum _{i=1}^n(y-(w_0+w_{1}x){)}^2$$

• 损失函数求导:
  $$\begin{gathered} loss=\frac{1}{2}\sum _{i=1}^n(y-(w_0+w_{1}x){)}^2 \\ =\frac{1}{2}\sum _{i=1}^n(y^2-2y(w_0+w_{1}x)+(w_0+w_{1}x{)}^2) \\ =\frac{1}{2}\sum _{i=1}^n(y^2-2y{w}_0-2y{w}_{1}x+w_0^2+2w_0{w}_{1}x+w_1^2{x}^2) \end{gathered}$$
  有：
  $$\begin{gathered} \frac{\partial loss}{\partial w_0}=\frac{1}{2}\sum _{i=1}^n(0-2y-0+2w_0+2w_{1}x+0) \\ =\sum _{i=1}^n-y+(w_0+w_{1}x) \\ =\sum _{i=1}^n-y+y^{\prime } \\ =\sum _{i=1}^n-(y-y^{\prime }) \end{gathered}$$
  $$\begin{gathered} \frac{\partial loss}{\partial w_1}=\frac{1}{2}\sum _{i=1}^n(0-0-2yx+0+2w_{0}x+2w_1{x}^2) \\ =\sum _{i=1}^n-yx+w_{0}x+w_1{x}^2 \\ =\sum _{i=1}^{n}x(-y+w_0+w_{1}x) \\ =\sum _{i=1}^n-x(y-y^{\prime }) \end{gathered}$$

模型实现并可视化

• 不使用sklearn

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d

# 准备数据
train_x = np.array([0.5, 0.6, 0.8, 1.1, 1.4])
train_y = np.array([5.0, 5.5, 6.0, 6.8, 7.0])

epoch = 500 # 迭代次数
learning_rate = 0.001 # 学习率
epoches = [] # 连续记录迭代次数
losses = [] # 连续记录损失值
w0, w1 = [1], [1] # 线性模型初始值 

for idx in range(1, epoch+1):
    epoches.append(idx)
    y = w1[-1]*train_x + w0[-1] # y=w1*x + b
    # 根据线性模型构建损失函数
    loss = ((train_y-y)**2).sum() / 2
    losses.append(loss)
    print('%d:w1=%f, w0=%f, loss=%f'%(idx,w1[-1],w0[-1],loss))
    # 计算梯度
    grad_w0 = -(train_y-y).sum()
    grad_w1 = -(train_x*(train_y-y)).sum()
    # 更新参数
    w0.append(w0[-1] - grad_w0 * learning_rate)
    w1.append(w1[-1] - grad_w1 * learning_rate)
"""
...
497:w1=2.972435, w0=3.356704, loss=0.261574
498:w1=2.972407, w0=3.357141, loss=0.261382
499:w1=2.972378, w0=3.357577, loss=0.261192
500:w1=2.972347, w0=3.358011, loss=0.261004
"""

print('--------损失值可视化--------')
plt.figure('Linear Losses', figsize=(8,8), dpi=50, facecolor='gray')
plt.title('Losses', fontsize=20)
plt.plot(epoches, losses, color='red')
plt.xlabel('epoches', fontsize=20)
plt.ylabel('losses', fontsize=20)
plt.grid(linestyle=':') # 显示网格线
plt.tight_layout() # 设置紧凑格式
plt.legend(['losses'], borderpad=1.5, fontsize=20)
plt.show()

print('--------线性模型可视化--------')
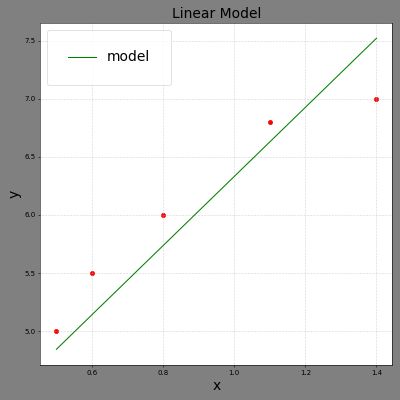
plt.figure('Linear Model', figsize=(8,8), dpi=50, facecolor='gray')
plt.title('Linear Model', fontsize=20)
plt.plot(train_x, train_x*w1[-1]+w0[-1], color='green')
plt.xlabel('x', fontsize=20)
plt.ylabel('y', fontsize=20)
plt.scatter(train_x, train_y, c='red')
plt.grid(linestyle=':') 
plt.tight_layout() 
plt.legend(['model'], borderpad=1.5, fontsize=20)
plt.show()

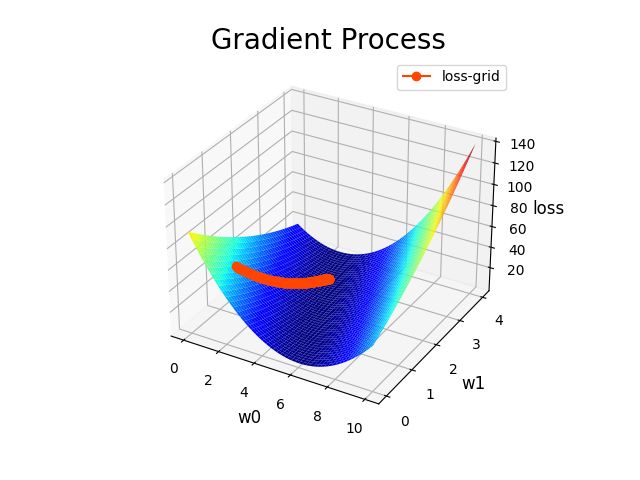
print('--------梯度下降过程可视化--------')
arr1 = np.linspace(0,10,500) # [0,9]产生500个数据
arr2 = np.linspace(0,4,500) # [0,3]产生500个数据
# 利用arr1和arr2组合成二维矩阵，grid_w0, grid_w1均为二维矩阵且分别存储每一个点的x,y值
grid_w0, grid_w1 = np.meshgrid(arr1, arr2)
# 将grid_w0,grid_w1拉成一维
flat_w0, flat_w1 = grid_w0.ravel(), grid_w1.ravel()
train_y_re = train_y.reshape(-1, 1) # 置为二维矩阵
outer = np.outer(train_x, flat_w1) # 求解外积
flat_loss = ((flat_w0 + outer - train_y_re)**2).sum(axis=0) / 2 # 计算损失
grid_loss = flat_loss.reshape(grid_w1.shape)

ax = plt.gca(projection='3d')
plt.title('Gradient Process', fontsize=20)
ax.set_xlabel('w0', fontsize=12)
ax.set_ylabel('w1', fontsize=12)
ax.set_zlabel('loss', fontsize=12)
ax.plot_surface(grid_w0, grid_w1, grid_loss, rstride=10, cstride=10, cmap='jet')
ax.plot(w0[0:-1], w1[:-1], losses, 'o-', c='orangered', label='loss-grid', zorder=5)
plt.legend(loc='upper right')
plt.show()

• 使用sklearn

import numpy as np
import sklearn.linear_model as lm
import sklearn.metrics as sm # 模型性能评价模块

train_x = np.array([[0.5], [0.6], [0.8], [1.1], [1.4]])
train_y = np.array([5.0, 5.5, 6.0, 6.8, 7.0])

# 创建线性回归器
model = lm.LinearRegression()
# 训练线性回归器
model.fit(train_x, train_y)
# 根据模型预测输出
pred_y = model.predict(train_x)

print('coef_:', model.coef_) # 系数
print('intercept_:', model.intercept_) # 截距
"""
coef_: [2.2189781]
intercept_: 4.107299270072993
"""

模型评价指标

• 平均绝对误差：单个观测值与算术平均值的偏差的绝对值的平均；
• 均方误差：单个样本到平均值差值的平方平均值；
• 中位数绝对偏差：单个样本与数据中值绝对偏差的中值；
• R2决定系数：越趋向于1，模型越好；越趋向于0，模型越差。详细计算放在下次吧。。。