数学建模30种基本模型_数学建模笔记——评价类模型之层次分析法

全国数学建模大赛再过一段时间就要开始了，没参加过比赛的小白决定试一试。不过小白本白建模经历较少，水平一般，只能不断学习来弥补一下了。今天学校也开始了数学建模培训，经过几个小时的学习之后……我决定还是先看一些简单的偏应用的建模方式吧。嗯，所以就从哔哩哔哩上找到一个数学建模课程学习。ok，废话不多说，直接开始啦~

这套课程主要讲解了十个模型，并讲解了相应的常用算法，今天就学习一下第一个模型——评价类模型吧。

简介

评价类模型应该是最基础的模型之一了，往往对应着生活中一些很实际的问题。例如，高考结束了，你是选择南大还是武大呢？已知今天空气中几种污染气体的浓度，如何确定空气质量等级呢？放假想要出去旅游，有好几个备选目的地，如果只能选一个，该去哪里呢？这些都是典型的评价类问题，其目的往往是按照一定的规则在许多方案中选择一个最好的方案，本质上就是对各种方案做出评价。

对评价类问题建模，往往需要考虑三个方面：

1. 评价的目标是什么？
2. 达成目标的方案有哪些？
3. 评价的指标/准则是什么？

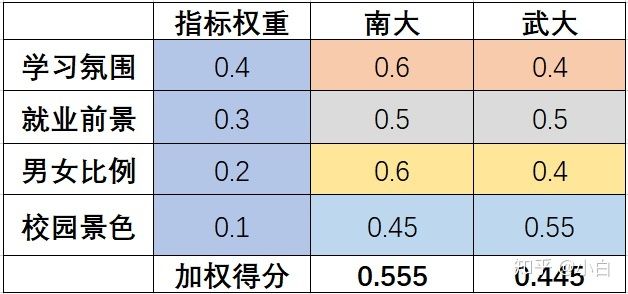
例如，高考后选择南大还是武大呢？评价的目标就是选择学校，达成目标的方案就是选择南大或者选择武大，相关的指标有学科实力，校园景色，男女比例等等。

我们可以如何解决上述问题呢？一个好的方法就是列个表格打打分，如图所示。

我们可以给予评价指标不同的权重，之后按照每个指标给南大和武大打分，最后再加权求和，便可以给出两个学校比较合理的得分，作为我们评价的最终结果。之后便选择得分更高的那个学校去上学啦~

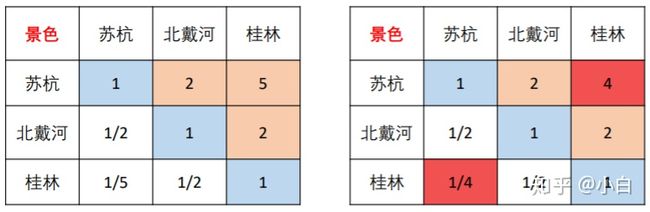
考虑到对于不同的评价问题存在不同的指标，其量纲往往是不同的，不一定都是以分数都是衡量标准。因此对于某个指标，给不同的方案进行打分时，我们依然以“权重”作为其衡量的标准，其权重之和为1即可。如上图所示，相同颜色的单元格和为1，指标权重比较好理解，给予指标以不同的权重以加权。打分也是以“权重”来衡量，南大在学习氛围方面是0.6，武大便是0.4。如果再加一个东南，那学习氛围方面可能就是0.3，0.25，0.45，其加和依然是1。当然，我们也可以将正常打分作为衡量标准，例如学习氛围分数分别为95，90。但是为了整体更方便计算，这里选择“权重”作为衡量的标准，特此说明。

解决评价类模型的方法有四种，分别是层析分析法，TOPSIS法，模糊综合评价法，灰色关联分析法。其原理各有差别，但是大体上都是差不多的，也就是通过加权求和进行打分，最后选出最高分。区别便是不同的方法里，“分数”的表示不太相同，我们慢慢谈。

层析分析法

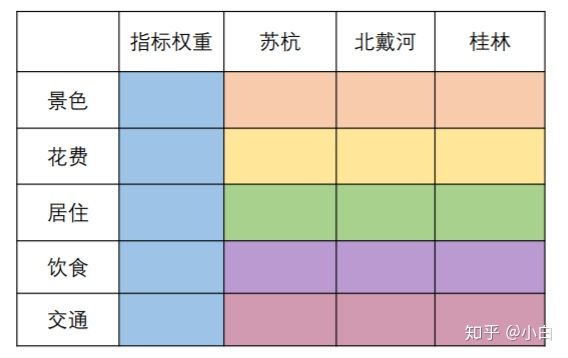
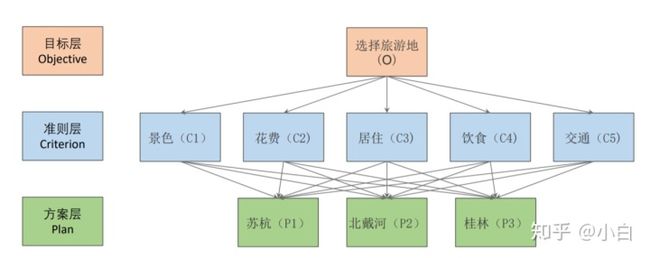
ok，先介绍第一个方法，层次分析法，简称AHP，主要用于解决各种评价类问题。其适用对象往往是，不给出具体指标及指标权重，也不给出每一种方案在指标内部的权重。例如，小明想去旅游，有苏杭，北戴河，桂林三个城市可以选择，请确定评价指标，形成评价体系为小明选择最佳方案。看，这个题干就是光秃秃的，给三个方案，选择最好的，什么指标和权重都没给，这也是层次分析法比较适合的题目类型。

遇到问题不要慌，大喊一声奥力给……啊不是，遇到这个问题想一想我们解决的一般方法。首先确定目标，嗯，选择旅游目的地；之后看看有哪些方案，嗯，题目给了，有三种；再想想评价指标是什么？嗯，题目没给，需要解决这个困难。

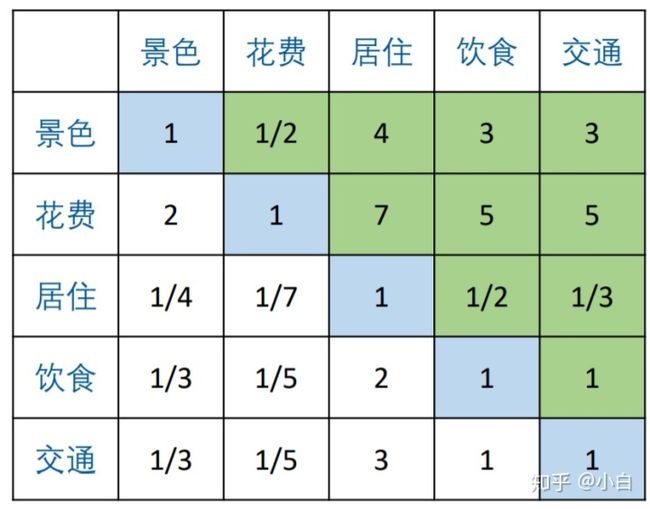
对于没有给出评价指标的问题，我们可以结合生活常识，或者他人已经完成的研究来设定评价指标。例如我们自己去旅游时，会考虑景色，住宿价格，交通等等。有时候自己考虑不太全面，需要参考别的研究中用到的指标，可以去知网等论文平台进行查询。如图。

假如没有找到相关文献，那就小组头脑风暴吧，或者知乎百度走一走，总能找到相对比较全面的评价指标。这里我们选择景色，花费，居住，饮食，交通作为衡量旅游目的地的指标。

解决了指标问题，我们就要开始打分了。但是我们这个时候没有指标权重，同一指标下也没有各种方案的打分。这个时候就需要获得这些数据。如何获得呢？可以直接问小明，“小明小明，你来给指标排个序，顺便给方案打个分吧”，这样当然可以，但是建模比赛时，没有小明给你问，发问卷调查太耽误时间，自己随便填又显得很不专业。而且对于同一个人来说，同时面对五个指标进行权重排序，由于指标较多，不同的时间点往往有不同的答案，因此也不太稳定，今天我觉得是0.2，0.2，0.3，0.2，0.1，明天可能就觉得是0.2，0.3，0.2，0.1，0.2了。嗯，这就是为什么要用到层次分析法了。既然一次性考虑五个指标容易出现变卦行为，且建模中凭感觉给数字也不太可靠，那我们就用一个比较科学又显得又水平的方法进行权重分配，也就是层次分析法。

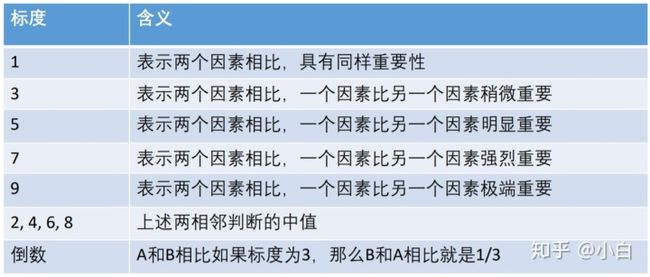
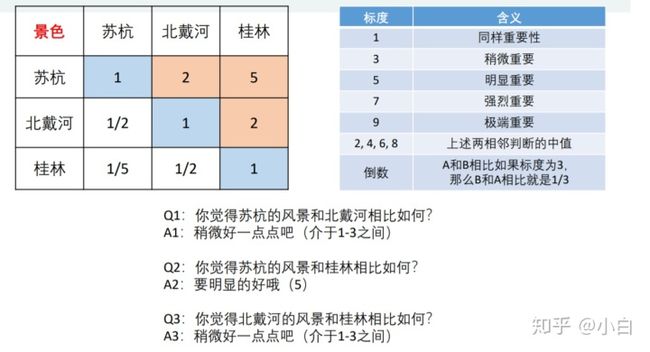
层次分析法的思想如下：对于多个指标，我们可以两个两个进行比较评价，根据两两比较的结果来判断权重。为了进行量化，层次分析法使用了九个等级18个数字来比较两个指标之间的重要性（满意度），如下图。

举例说明，假如有一个小明在你面前，你就可以问他，“小明小明，你觉得对于旅游景点而言，花费和景色哪个更重要？重要程度是多少？”利用上图的重要程度进行量化，如果小明觉得，感觉花费比景色稍稍重要一点点，嗯，稍稍重要一点儿，那应该是介于同等重要和稍微重要之间吧，那花费对景色的标度就是2，景色对花费的标度就是1/2，也就说明花费应该比景色稍微具有更高的权重。具体填写时，没有小明回答你，因此往往就问队友或者自己。同样，对于“稍微重要一点点”，不同的人理解的程度就不同，可能就有人觉得，应该介于“稍微重要”和“明显重要”之间，那此时花费对景色的标度就是4，这个因人而异啦。

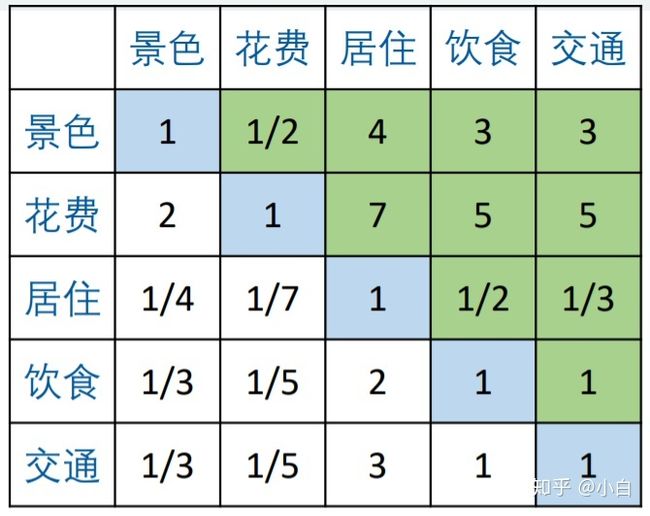
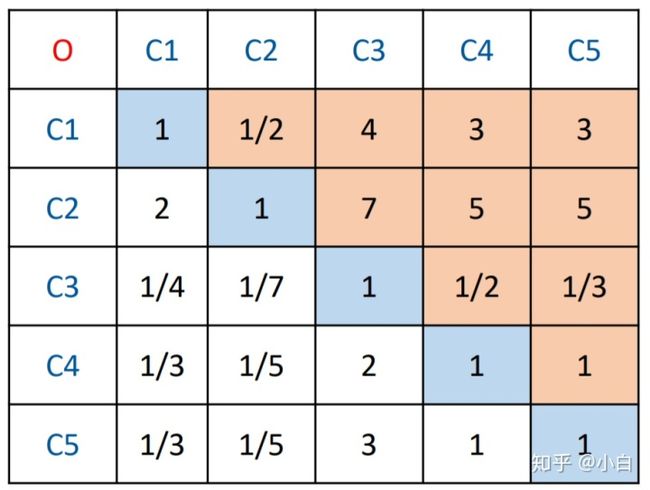
按照上面的问法，两两比较，也就是

次询问，并给出相应的标度。可以发现，两两比较要比五个一起比较更为准确稳定，同时给出了九个等级的量化指标，比直接凭感觉填写又要准确一些。为了方便记录以及接下来的运算，我们使用矩阵的形式记录结果，这个矩阵也被称之为判断矩阵。

这是一个5×5的方阵，所有的判断矩阵都是方阵，我们记为

，对应的元素为

，其中

的意思是与指标

相比，指标

的重要程度。例如矩阵中

，花费相对于交通，就是明显重要。实际意义上就代表我们可以为了节省花费而选择更便宜的交通。判断矩阵主对角线元素都是1，也就说明相同指标是一样重要的。同时，

且

，我们称满足这一条件的矩阵为正互反矩阵。

这个判断矩阵在形成的过程中，有可能出现某种不一致的现象。例如假设你觉得居住比饮食重要，又觉得饮食比交通重要，但是在居住和交通比较时，又觉得交通比居住重要，这就出现了重要程度的不一致现象。由于重要程度可以用数字量化，因此在比较的过程中也会出现传递性。上述的判断即是不满足传递性。

这里我们引出一个概念，一致矩阵。我们可以定义

，

，那么

。这种定义方式是合理的，因为我们用1~9量化指标

对指标

的重要程度时，隐含了将指标

的重要程度设为1的假设。而如果一个正互反矩阵，满足

，我们称这样的矩阵是一致矩阵。这里给出两个矩阵，一个是一致矩阵，一个不是。

如果一个判断矩阵是一致矩阵，那么我们应用层次分析法，从形式逻辑上看无疑是最为成功的。因为在层次分析法的框架下，重要程度之间的比较满足

理应满足这种关系，如果我们的判断矩阵刚好是一致矩阵，那我们对重要程度的衡量在形式上是十分准确的。但如果我们的判断矩阵最终和一致矩阵不同，那就说明我们在判断的过程中，心理预期方面存在一定的偏差。因为我们的心理预期应该并不满足上述的乘法关系，我们往往凭感觉而不是数据进行判断。所以对于判断矩阵，我们也需要进行一定的检验——一致性检验。一致性检验用来检测判断矩阵与一致矩阵的偏差度，如果偏差在接受范围内，那么我们可以接受这个判断矩阵作为我们心理预期的量化指标。如果偏差无法接受，那则说明，我们在层次分析法的框架下，对于心理预期的量化是失败的。如果还想运用层次分析法解题，就要重新判断了。

接下来就是如何对判断矩阵进行一致性检验，也就是检测判断矩阵与一致性矩阵的偏差。由于个人能力以及篇幅问题，这里不对检验的原理进行证明，直接给出一致性检验的步骤。不过依然给出一个引理作为参考。

由引理大概可以感受到，判断一致性需要将判断矩阵的最大特征值与阶数进行比较。一共需要三步：

1. 计算一致性指标CI
   ，其中
   为判断矩阵最大的特征值（如果特征值中有虚数，比较的是特征值的模长），
   是判断矩阵的阶数。
2. 查找对应的平均随机一致性指标RI，直接查表就好了

3.计算一致性比例CR

之后就可以下判断了，如果CR<0.1，则认为判断矩阵的一致性可以接受，否则需要对判断矩阵进行修正，也就是尽量往一致矩阵去调整。

嗯，以上一致性检验仅给出了步骤，具体的原理，感兴趣可以自行查阅。这里提出一个小问题，如果

，RI=0，可怎么办？

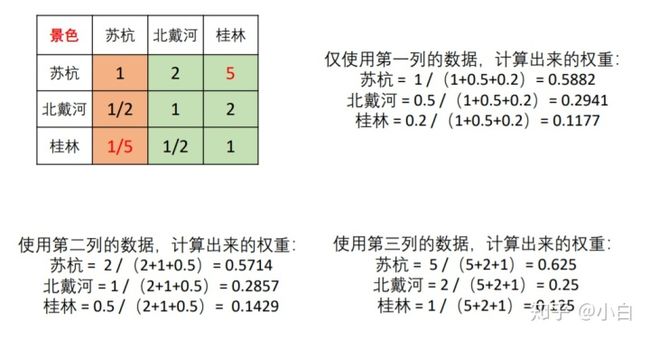
嗯，进行了一致性检验之后，我们可以计算各个指标的权重了。总算到这一步了。到这里其实就很简单了，因为通过了一致性检验的判断矩阵，较为成功地对我们的心理预期进行了量化，也就是很大程度上，正确地反映了我们对不同指标重要性的判断，完全可以把矩阵中一列的数字看作重要程度的“打分”了。但这个时候不看成权重，为什么呢？因为加起来不是1啊。

举个例子，对于矩阵中的某一列，由于

在给出时假设了指标

的重要程度为1，其余指标的重要程度也就是以指标

为基准了，这个时候可以直接对列进行归一化处理，计算权重。假设上面的判断矩阵已经通过一致性检验，从第一列来看，景色的权重应该为

，其他指标同理。此时是以景色的重要程度作为1来看待的，如果以花费的重要程度作为1来看待，那么景色的权重应该是

。按照这个方式，以不同的指标的重要性作为基准1时，同一指标的权重可能是不同的。例如景色在第一列的权重是0.2553，第二列就是0.2448，每一列应该都有一个权重，那怎么取舍呢？很自然的想法就是取平均数嘛。

相信有些人已经意识到，如果判断矩阵是一个一致矩阵，同一指标在每一列的权重都是相同的。

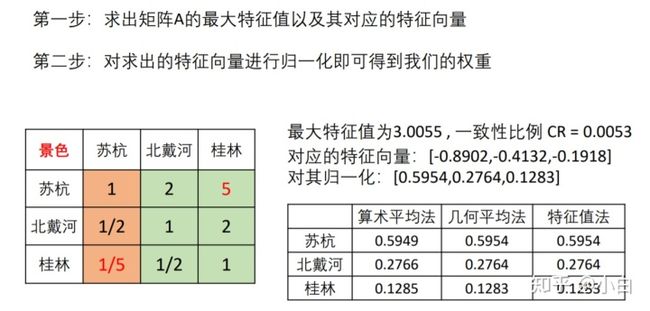
我们通过三种不同的方法计算权重，分别是算术平均数求权重，几何平均数求权重，特征值法求权重。上面已经对算术平均数法求权重给出了解释。几何平均数就是对数据进行一个几何平均啦，特征值法求权重就是求出判断矩阵最大特征值的特征向量，对他进行归一化处理求得权重。具体的原理可以自行查阅。

下面是特征值法求权重例子

一般而言，我们都是使用三种方式分别计算，最后再一次加权。嗯，不断地加权。

至此，我们总算把指标的权重求出来了。其实方法还蛮简单的，不过写起来好费劲哦，是我太啰嗦了吗……

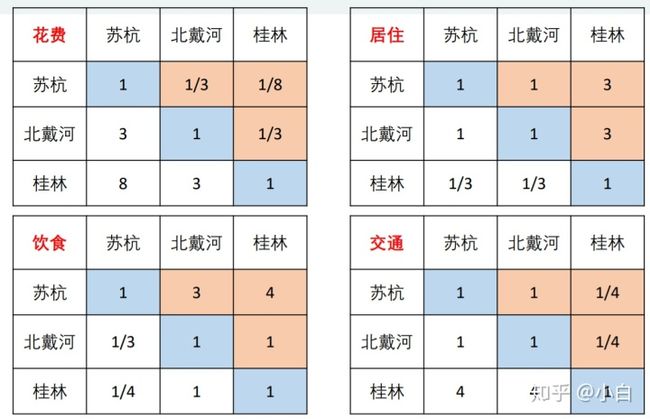
ok，我们继续打分，现在指标的权重已经有了，还缺什么呢？缺的是对于某一个指标，不同的方案在此指标下的评价。例如对于景色，满分一百分，我们可以给苏杭打98分，北戴河80分，桂林90分。这样依次对每一个指标进行打分，最后加权求出总分即可。

不过上面我们已经说过，我们最好使用“权重”作为打分的标准。如果直接凭感觉打分，那苏杭的“权重”就是

，以此类推。但是我们既然已经学了层次分析法，何不使用上面的两两比较的方法，给出同一指标下，不同方案的“满意程度”的判断矩阵呢？

如图所示，我们依然通过相同的重要性量化等级对上面的判断矩阵进行填写。这里我们把重要程度理解为满意度，数值越大，满意程度越大。上面的判断矩阵表明，填写者认为苏杭的景色比北戴河好，北戴河的景色比桂林好。之后对这个判断矩阵进行一致性检验，计算权重，即可作为不同方案的评分。

其他的指标也以此类推。

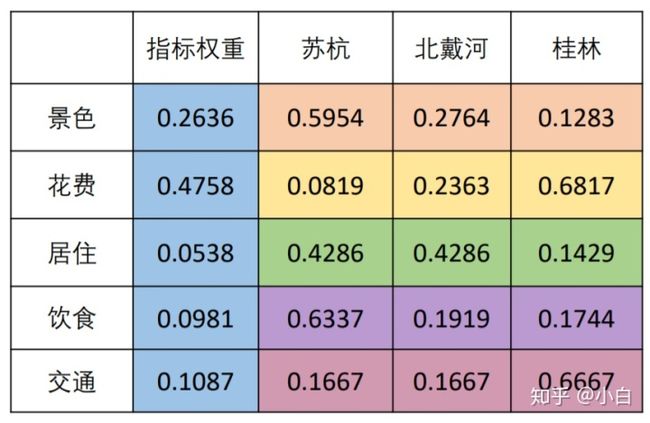
最后，经过一番努力，我们给出了一张打分表。

加权计算得分，苏杭0.299，北戴河0.245，桂林0.455。嗯，小明去桂林。

嗯，最初我们只有一个很短的题目，但是通过这种简单的建模方式，我们给出了合理地可以让人信服的结果。感觉还是蛮有意思的。

总结

最后总结一下层次分析法的步骤。

1. 分析系统中各因素的关系，建立系统层次结构

其实也就是看看目标是什么，有哪些评价指标，有哪些方案。 2. 对于同一层次的各元素关于上一层次中某一准则的重要 性进行两两比较，构造两两比较矩阵（判断矩阵）

也就是按照文中讲的，计算指标的权重，计算方案的分数。 3. . 由判断矩阵计算被比较元素对于该准则的相对权重， 并进行一致性检验（检验通过权重才能用） 4. 根据权重矩阵计算得分，并进行排序 总结完毕。

局限性

主要两个局限性： 第一，判断矩阵阶数不能太多，上文中提到的

往往只给到

，当需要比较的指标或者方案太多时，判断矩阵和一致矩阵差异往往会比较大 第二，如果决策层数据已知，我们就不能用量化的重要程度进行打分了。有数据当然要用数据呀~也就是之后的TOPSIS法和模糊综合评价法。

拓展

上文中我们介绍的旅游系统只有三层，那如果有四层五层怎么搞？其实整体思想很简单啦，加权加权再加权，只要我加的够多，阶数就追不上我。

上文中，每个指标下都有三种方案，也就是北戴河，苏杭，桂林都具有景色，花费这五种指标，但有些问题中，每种指标对应的方案不完全重合，怎么搞？

其实你也知道的，分别加权呗……

hhh今天学到了什么？加权！

对了，这里可以推荐一下我听的课程，清风老师的数学建模课，哔哩哔哩上有试听课，播放量最多的数学建模课就是它。以及可以关注相应的微信公众号“数学建模学习交流”，听得感觉还不错~

下次再见~

欢迎留言，欢迎给出写作意见，这次确实写得是太多了，感谢您看到这里。

这两天知乎给我推送了一些数学建模相关的问答，其中一个是数学建模相关书籍。我把高赞回答推荐的书的电子版找了一下，如果需要的话，在微信公众号“我是陈小白”后台回复“数学建模书籍”即可。