【字符串处理Python实现】认真看完这篇文章，还不能彻底搞懂KMP算法你顺着网线来打我！

通过【字符串处理Python实现】字符串模式匹配之暴力、BM算法简介与实现，我们分别介绍了暴力算法和BM算法，其中：

• 暴力算法在每一轮发生字符匹配失败后，都只是简单粗暴地将模式串向右再滑动一个字符的长度，因此虽然最简单直观，但是不可避免会做很多无意义的比较；
• BM算法通过镜像试探和字符跳跃试探，可以在每一轮发生字符匹配失败后，尽可能多地向右滑动几个字符，从而减少无谓的比较。

本文将介绍另外一种大名鼎鼎且高效的字符串匹配算法——KMP算法，该算法由D. E. Knuth、J. H. Morris和V. R. Pratt三人共同提出，因此名字也就是三人姓氏的首字母。

一、名词术语

为了后续描述方便，在介绍KMP算法之前，这里先介绍几个关于字符串的几个名词和术语，假设给定某字符串'GTGT'，则：

• 前缀子串：''、'G'、'GT'、'GTG'和'GTGT'称为字符串'GTGT'的前缀子串；
• 真前缀子串：除去'GTGT'自身外的''、'G'、'GT'、'GTG'称为字符串'GTGT'的真前缀子串；
• 后缀子串：''、'T'、'GT'、'TGT'和'GTGT'称为字符串'GTGT'的后缀子串；
• 真后缀子串：除去'GTGT'自身外的''、'T'、'GT'、'TGT'称为字符串'GTGT'的真后缀子串。

本文为表述方便，后续提及的所有前缀子串和后缀子串均分别指真前缀子串和真后缀子串。

二、算法详述

首先，一句话总结KMP算法的核心思想：充分利用模式串当前这一轮和主串成功匹配的前若干个字符，使得在下一轮匹配前，模式串可以相对于主串向右再滑动尽可能多的字符数。

1. KMP算法流程概述

接下来，我们先通过实际的案例来直观阐释KMP算法具体的匹配过程，假设主串为'GTGTCGTTGGGTGTG'，模式串为'GTGTCGTG'。

同暴力以及BM匹配算法一样，KMP算法在匹配前，第一步也是将主串和模式串在最左侧对齐，然后从左往右逐字符进行比较。

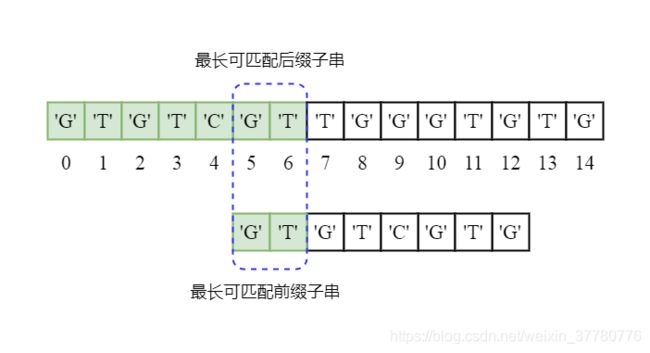
第一轮，如下图所示，我们发现此时模式串的前7个字符都和主串对齐位置的字符相同，直到第8个字符二者不一致。

现在的问题是，如何充分利用已匹配的子串'GTGTCGT'。首先，通过分析我们可以发现，'GTGTCGT'的前缀子串和后缀子串有这样的特点：

• 长度为1的前缀子串和其长度为1的后缀子串相同，均为'G'；
• 长度为2的前缀子串和其长度为2的后缀子串相同，均为'GT'；
• 除此之外，不存在其他长度相同的情况下，使得'GTGTCGT'的前缀子串和后缀子串相同。

我们将满足上述条件的子串'GT'称为'GTGTCGT'的最长可匹配前后缀子串。

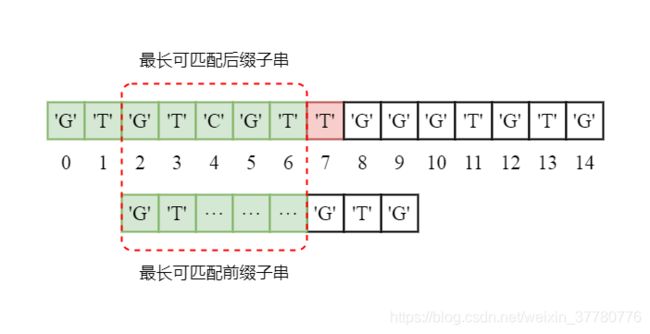
接下来，有了这个信息之后，KMP算法的精髓在于，可以将模式串和主串已匹配的前7个字符向右移动，直到最长可匹配前后缀'GT'对齐，如下图所示。这里我们直接将模式串向右又滑动了5个字符：

这里，有些人可能会有疑问，针对当前已成功匹配的子串为'GTGTCGT'，已知其最长可匹配前后缀子串为'GT'，为什么一定可以将模式串直接向右滑动5个字符后，使得最长可匹配前缀子串和最长可匹配后缀子串对齐的情况下，同时确保不漏掉中间可能成功匹配的情况？如：将模式串向右滑动两个字符，使得模式串和主串在后者索引为2的位置对齐（如下图所示）。

解答这个问题可以使用反证法来证明：

假设将模式串相对于主串向右滑动两个字符后，此时模式串处于可能和主串成功匹配的位置，这意味着至少从主串索引2到6的位置，模式串和主串对齐的字符需要相同，然而这时最长可匹配前后缀子串就不应该是'GT'了，而应该是'GTCGT'，这和实际矛盾，因此，假设不成立。

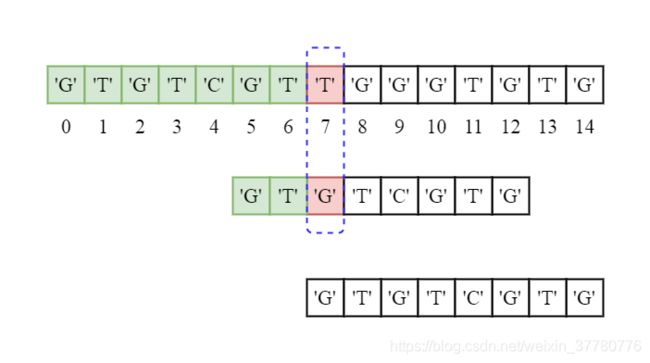
第二轮，如下图所示，我们发现此时模式串的前2个字符都和主串对齐位置的字符相同，直到第3个字符二者不一致。

此时，由于已匹配的子串为'GT'，显然，该子串的最长可匹配前后缀子串长度为0，可以认为此时已匹配子串'GT'的最长可匹配前后缀子串为''，因此，可以直接将模式串向右再滑动两个字符。

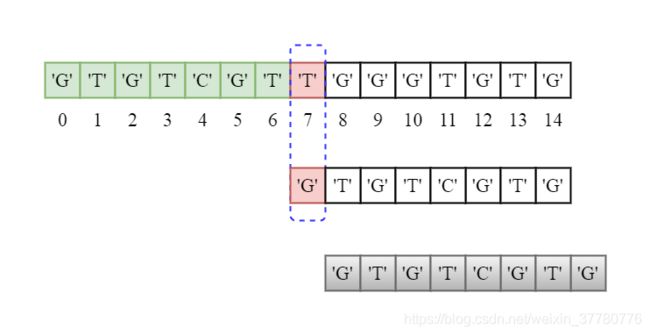
第三轮，如下图所示，我们发现此时模式串的第1个字符就已经和主串对齐位置的字符不相同，接着继续将模式串向右滑动一个字符，可以发现模式串尾部已经超出主串尾部，此时可判定匹配失败。至此，KMP算法的完整流程走完。

2. 引入前后缀子串数组

通过上面的案例，你可能已经隐约有所了解，实现KMP算法的重点在于：如何根据每轮成功匹配的子串：

• 先找到该子串的最长可匹配前后缀子串；
• 然后确定该最长可匹配前后缀子串的长度；
• 最后，利用该长度，在下一轮匹配前，确定向模式串右滑动的字符数。

乍一看，每一轮匹配后，都需要在得到主串和模式串的部分匹配子串后，确定该子串的最长可匹配前后缀子串。实际上，结合上述KMP算法的匹配流程，我们知道每一轮匹配得到的部分子串都是模式串的前缀子串。

因此，仅通过模式串，通过列出主串和模式串的所有可能的部分匹配子串¹，可以预先确定各部分子串最长可匹配前后缀子串的信息，并将其保存在一个数组pi中²。

该一维数组的下标代表了部分匹配子串的长度，对应下标处的值则是部分匹配子串中，最长可匹配前后缀子串的长度。

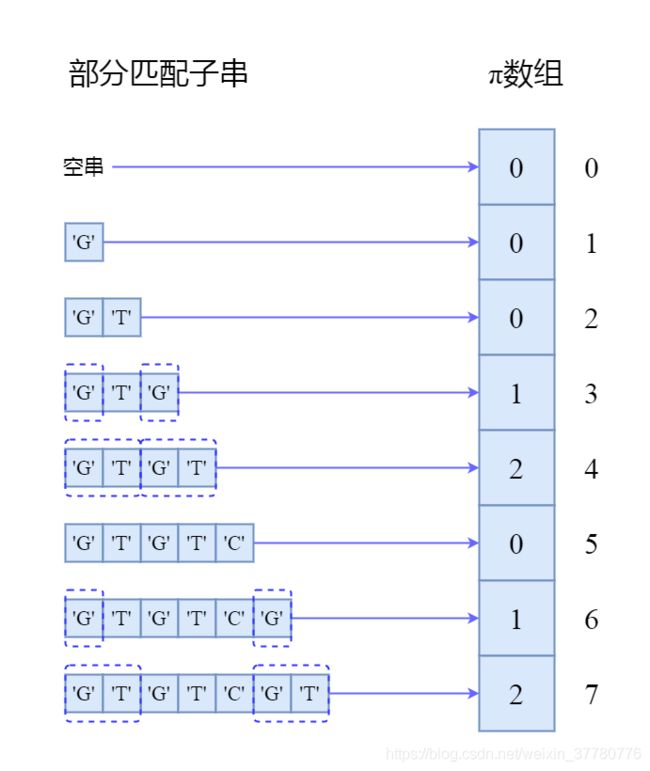
上面对于pi数组的描述非常拗口，下图是上述模式串'GTGTCGTG'的对应的pi数组：

具体地：

• 当部分匹配子串为''时，此时其长度为0，且最长可匹配前后缀子串可视为''，其长度为0，因此pi[0] = 0；
• 当部分匹配子串为'G'时，此时其长度为1，且最长可匹配前后缀子串可视为''，其长度为0，因此pi[1] = 0；
• 当部分匹配子串为'GT'时，此时其长度为2，且最长可匹配前后缀子串可视为''，其长度为0，因此pi[2] = 0；
• 当部分匹配子串为'GTG'时，此时其长度为3，且最长可匹配前后缀子串为'G'，其长度为1，因此pi[3] = 1；
• 当部分匹配子串为'GTGT'时，此时其长度为4，且最长可匹配前后缀子串为'GT'，其长度为2，因此pi[4] = 2；
• 当部分匹配子串为'GTGTC'时，此时其长度为5，且最长可匹配前后缀子串可视为''，其长度为0，因此pi[5] = 0；
• 当部分匹配子串为'GTGTCG'时，此时其长度为6，且最长可匹配前后缀子串为'G'，其长度为1，因此pi[6] = 1；
• 当部分匹配子串为'GTGTCGT'时，此时其长度为7，且最长可匹配前后缀子串为'GT'，其长度为2，因此pi[7] = 2。

3. 使用前后缀子串数组

上面我们通过人工的方式得到了前后缀子串数组，那么如何在使用KMP算法的时候应用该数组呢？

在使用KMP算法进行字符串匹配算法时，模式串在内存中并非真的会相对于主串“滑动”，所谓的滑动是通过辅助指针变量的更新来体现的：一般代码实现都是对主串和模式串分别使用一个指针变量i和j，然后在匹配过程中更新两个指针，而前后缀子串数组就是用来更新指向模式串的指针变量。

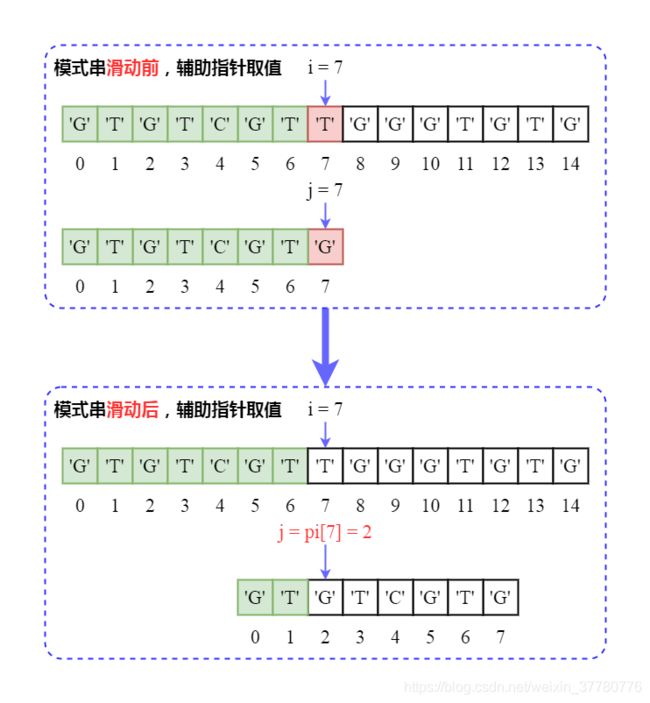
具体地，如下图所示：

• 第一轮匹配时，当i = 7和j = 7时发生不匹配，此时部分匹配子串长度为7，于是模式串滑动的代码体现是辅助指针j = pi[7] = 2；

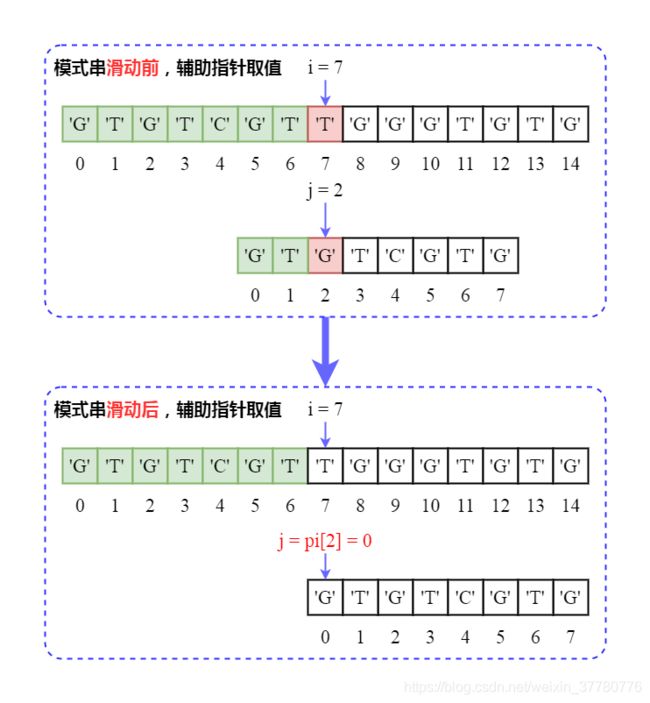
• 第二轮匹配时，当i = 7和j = 2时发生不匹配，此时部分匹配子串长度为2，于是模式串滑动的代码体现是辅助指针j = pi[2] = 0。

4. 生成前后缀子串数组

上面我们通过直接观察的方式得到了模式串的pi数组，下面介绍如何通过理论分析的方式得到该数组，也为后续实现生成前后缀子串数组的代码做准备，这里模式串用单词needle³来表示。

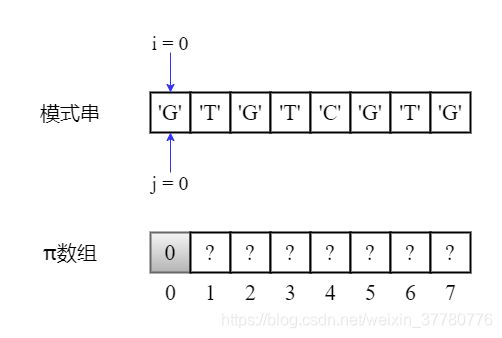
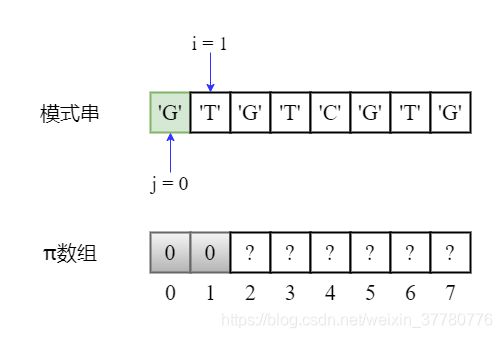
首先，如下图所示，我们使用两个指针变量i和j，其中i代表部分匹配子串下一个字符的索引，即pi数组的下标，j代表最长可匹配前缀子串下一个字符的索引，即pi数组的值。

• 一开始，因为部分匹配子串和最长可匹配前缀子串均可视为''，则初始化i = 0且j = 0，显然pi[0] = 0；

• 接着，将i加1，使得部分匹配子串的为'G'，长度为1，因此最长可匹配前后缀子串仍然可视为''，长度为0，由前述讨论易知pi[1] = 0；

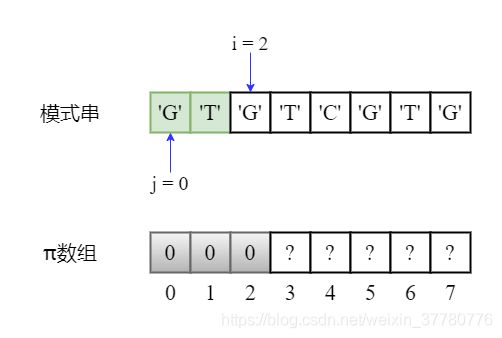
• 继续将i加1，使得部分匹配子串为'GT'，长度为2，此时needle[j] != needle[i - 1]，即'G' != 'T'，因此最长可匹配前后缀子串仍然可视为''，长度为0，因此pi[2] = 0；

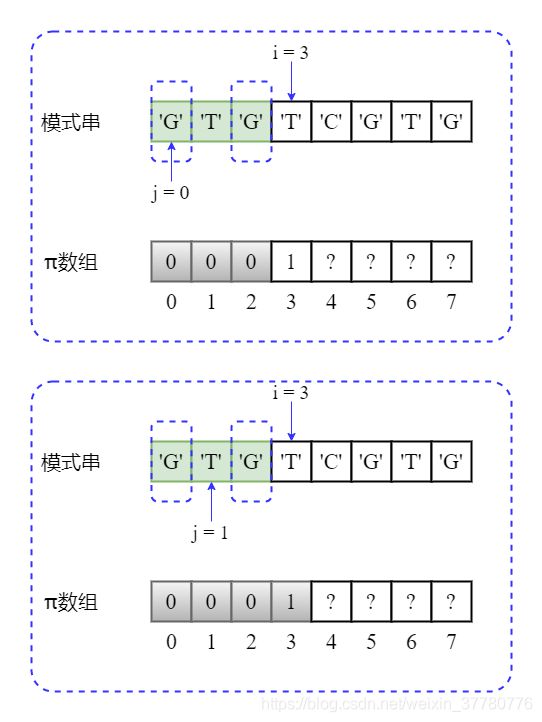
• 继续将i加1，使得部分匹配子串为'GTG'，长度为3；终于，此时needle[j] == needle[i - 1]，即'G' == 'G'，因此最长可匹配前后缀子串为'G'，长度为1，因此pi[3] = pi[2] + 1 = 1，且之后更新j += 1；

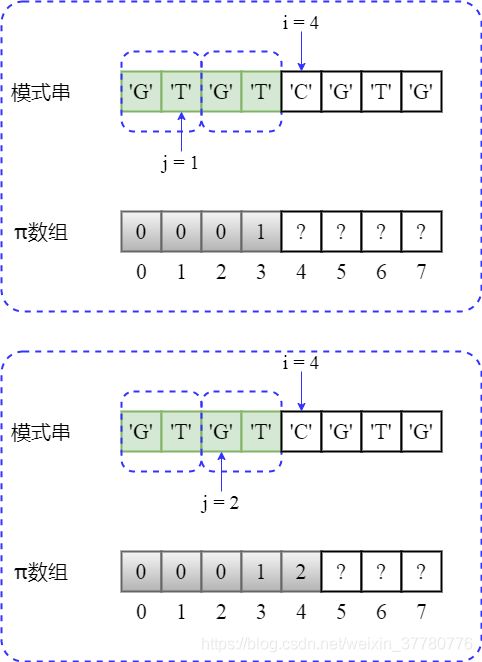
• 继续将i加1，使得部分匹配子串为'GTGT'，长度为4；此时needle[j] == needle[i - 1]，即'T' == 'T'，因此最长可匹配前后缀子串为'G'，长度为2，因此pi[4] = pi[3] + 1 = 2，且之后更新j += 1；

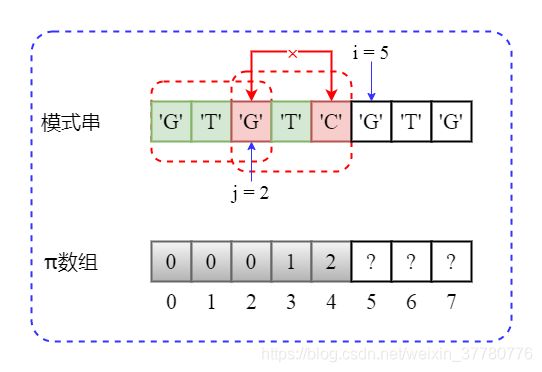
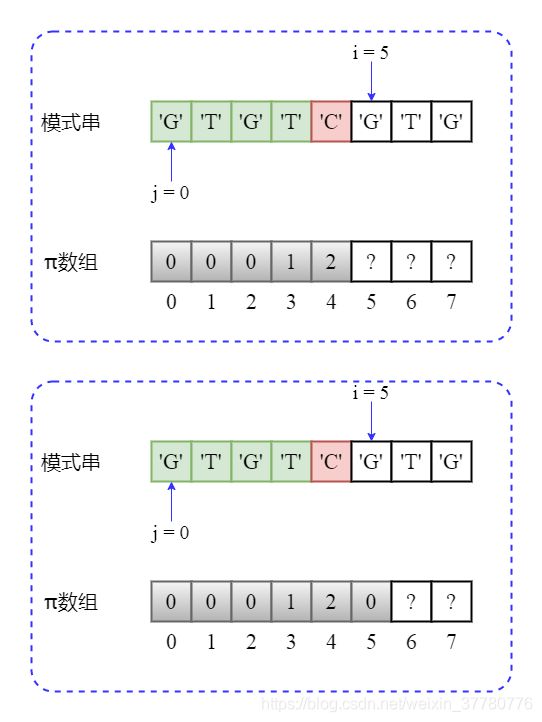
• 继续将i加1，使得部分匹配子串为'GTGTC'，长度为5；此时needle[j] != needle[i - 1]，即'G' != 'C'，因此最长可匹配前后缀子串为''，长度为0，但是此时无法直接通过pi[4]的值来推导得到pi[5]；

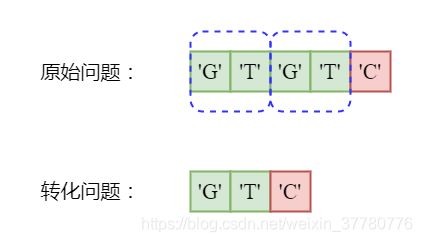
为了得到pi[5]的值，即计算部分匹配子串'GTGTC'的最长可匹配前缀子串，实际上可以将该问题转化为求解'GTC'最长可匹配前缀子串的问题：

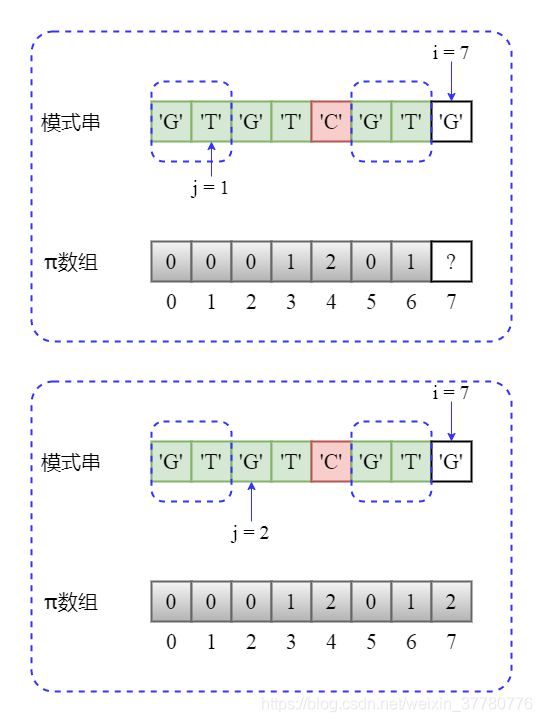
事实上，此时如下图所示，相当于将辅助指针变量j回溯到了j = pi[j] = pi[2] = 0，回溯后由于needle[j] != needle[i - 1]，即'G' != 'C'，此时j已经不能再回溯，所以pi[5] = 0。

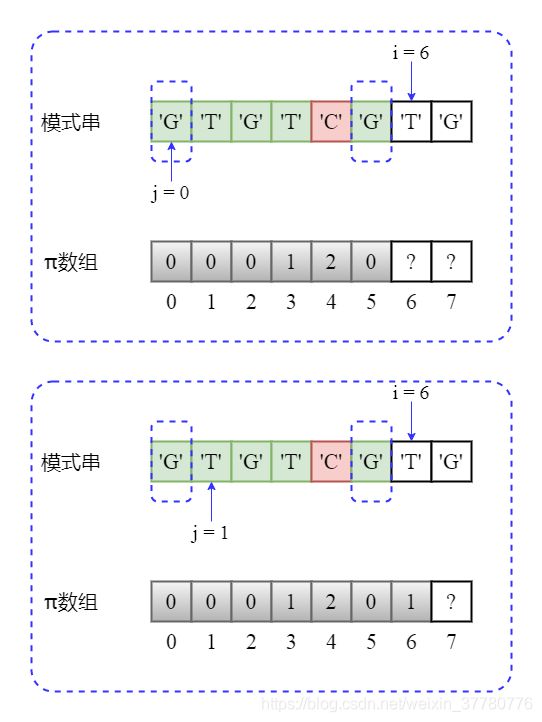
• 继续将i加1，使得部分匹配子串为'GTGTCG'，长度为6；此时needle[j] == needle[i - 1]，即'G' == 'G'，因此最长可匹配前后缀子串为'G'，长度为1，因此pi[6] = pi[5] + 1 = 1，且之后更新j += 1；

• 继续将i加1，使得部分匹配子串为'GTGTCGT'，长度为7；此时needle[j] == needle[i - 1]，即'T' == 'T'，因此最长可匹配前后缀子串为'GT'，长度为2，因此pi[7] = pi[6] + 1 = 2，且之后更新j += 1。

至此，我们通过计算的方式得到了pi数组。

三、算法实现

根据上述理论分析，下面以Python给出KMP算法的完整实现，为了提高代码的可读性并降低函数功能的耦合性，这里给出了两个函数：

• kmp_match函数可视为主函数，负责通过模式串needle在主串haystack中查找匹配，主要实现参考本文使用前后缀子串数组部分；
• compute_prefix_func用于预先计算pi数组，主要实现参考本文生成前后缀子串数组部分。

def kmp_match(haystack, needle):
    """KMP算法的主程序，haystack是主串，needle是模式串"""
    pi = compute_max_prefix(needle)  # 预处理，生成描述模式串子串最大可匹配前后缀子串的数组
    n, m = len(haystack), len(needle)
    j = 0
    for i in range(n):
        while j > 0 and haystack[i] != needle[j]:
            # 当发生不匹配时，查询pi数组，更新模式串指针变量j的值
            j = pi[j]
        if haystack[i] == needle[j]:
            j += 1
        if j == m:  # 匹配成功，返回下标
            return i - m + 1
    return -1


def compute_max_prefix(needle):
    """根据模式串生成pi数组"""
    m = len(needle)
    pi = [0] * m
    j = 0
    for i in range(2, m):
        while j != 0 and needle[j] != needle[i - 1]:
            # 回溯辅助指针j
            j = pi[j]
        if needle[j] == needle[i - 1]:
            j += 1
        pi[i] = j  # 最长可匹配前缀子串的下一个位置的索引等于其长度
    return pi


if __name__ == '__main__':
    haystack = "ATGTGAGCTGGTGTGTGCFAA"
    needle = "GTGTGCF"
    index = kmp_match(haystack, needle)
    print(index)

直觉上可知，在主串中存在较多重复字符的情况下，KMP算法的效率较高。

四、参考资料

• [1] 漫画：什么是KMP算法？
• [2] 「天勤公开课」KMP算法易懂版
• [3] （原创）详解KMP算法
• [4] KMP算法详解-彻底清楚了(转载+部分原创)

---

1. 假设模式串为needle的长度为m，这里的所有部分匹配子串是指needle[0:k]且$k\in [0,1,\cdot \cdot \cdot ,m-1]$。 ↩︎

2. 很多教程和书籍也将该数组称为next。 ↩︎

3. 后续在代码中将主串命名为haystack，这实际上用了英语中一句谚语"Search for a needle in a haystack."即“大海捞针”，只不过英语中字面意思是指“在一个干草垛中寻找一根针。”这里将在主串比喻为干草垛，将模式串比喻为针。 ↩︎