控制系统设计专题(一)——PID控制算法
前言
PID控制算法是工业控制领域数十年来应用最广泛的经典控制算法之一,其理论原理易于理解,算法结构简单,易于工程实现,这也是其受到工程师们青睐的重要原因。
尽管算法原理简单,其参数整定难度却因被控对象而异,不同工程师对同一被控对象整定出的PID参数也各不相同。这对PID控制算法的理解以及工程经验提出了很高的要求。本篇将从PID控制算法展开,针对PID控制算法的几个主要问题进行探讨。
PID控制算法原理
PID控制算法,是指由比例项(P-Proportional),积分项(I-Intergral),微分项(D-Derivative)的全部或部分组合的一种控制算法。它即可以适用于模型已知的被控对象,也可以用于模型未知的被控对象。本文以simulink仿真的形式说明PID控制算法的原理,具体的simulink模型如图1所示,实验中使用单位阶跃信号作为给定输入信号。

常用的PID控制算法主要分为:
- 比例控制算法(P)
该控制器由单一的比例环节组成,当输入单位阶跃信号时,其响应如图2所示。我们可以看到,纯比例控制器控制下的实验对象,存在稳态误差,当比例项系数增大时,该稳态误差会逐渐减小,但无法完全消除,这也是P控制器的弊端之一。
该控制器通常用于伺服系统,作为控制结构中的外环路控制器,例如多旋翼飞行器姿态控制回路中的角度外环,往往采用纯比例控制器进行闭环控制。
- 比例-积分控制算法(PI)
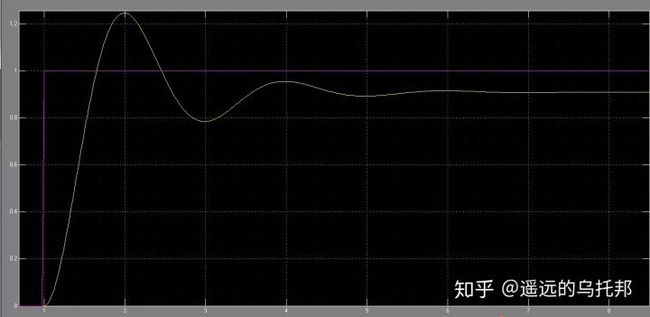
为了消除稳态误差,我们引入了比例环节,组成了比例-积分控制器,其单位阶跃响应如图3所示。该实验在比例项系数不变的情况下,增加了积分环节,可以看到,稳态误差被消除了,然而,其超调量增加了。引入积分项后,确实提高了稳态精度,然而,系统的动态响应受到影响。
该控制器常用于部分电机控制的速度环路,或其他对于稳态精度较高的被控对象。
- 比例-微分控制算法(PD)
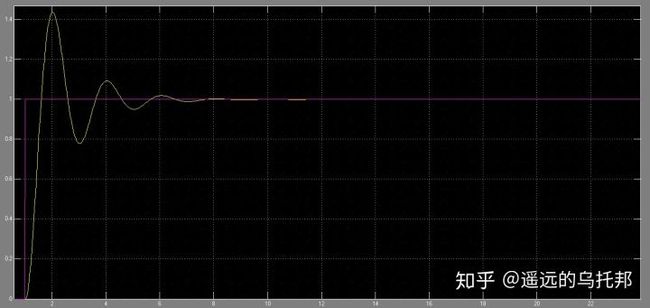
为了提高控制器的动态响应速度,引入了比例-微分控制器,如图4所示为PD控制器的单位阶跃响应。由图可知,加入微分项改善了系统的动态性能,减小了超调量,缩短了系统进入稳态的时间。
- 比例-积分-微分控制算法(PID)
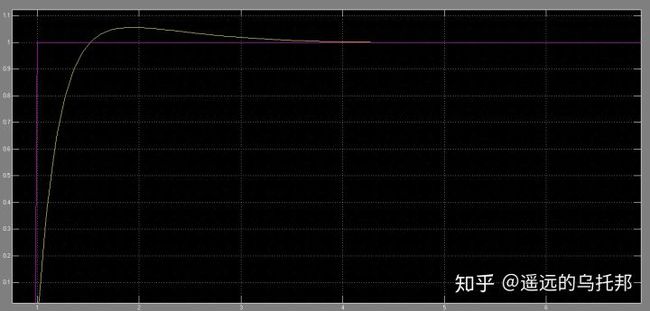
PID控制器则综合了比例-积分-微分三项,其单位阶跃响应如图5所示。通过整定合适的PID参数,能够兼顾动态性能与稳态性能。该控制器适用于几乎所有被控对象。实际工程使用当中由于被控对象模型的不同,参数整定的难度也不尽相同。
PID控制算法的几个主要问题
尽管PID能够满足许多工程领域的控制性能指标,然而,在实际使用过程中,我们发现了许多问题:
- 积分饱和现象
积分项的引入能够消除稳态误差,然而,其对于系统动态性能的影响也是不可忽视的。最常见的如积分饱和现象,就是一种典型的负面影响。
那么究竟什么是积分饱和现象?
当控制器持续无法消除误差时,积分项将持续向某一方向增大,直至达到限幅值;此时,若误差与积分项符号相反,积分项则严重影响到整个控制器的输出,从而导致被控对象动态性能下降,出现如滞后甚至震荡的现象。
对于许多系统而言,积分饱和现象是十分危险的,对于该现象,我们往往采用以下几种解决方法:
1. 积分限幅法
该方法通过对积分项设置上下限的方式,降低积分项在整个控制器输出当中的权重,以减轻积分饱和现象带来的负面影响。
2. 积分分离法
该方法对误差设置阈值,当误差大于设定阈值时,将积分项从PID控制器中分离,该方法可能存在控制输出突变的情况。
3. 变速积分法
该方法对积分项线性积分的方式采用非线性函数进行替换,使得积分项在不同的误差区间的积分速度发生改变,以适应不同的被控对象特性。
4. 遇限削弱积分法
该方法当控制器输出达到设定阈值时,不再对其进行积分,只有当积分项减小时,才继续进行积分。这样既能使得积分项起到应有的作用,又能减小超调量。
- 微分信号的生成问题
离散微分信号的生成往往通过差分来近似。然而,由于差分信号容易将噪声一起放大,从而导致这样计算的微分信号信噪比下降,这对于微分控制非常不利。因此,我们可以通过跟踪微分器的方式生成微分信号,具体的推导和原理将在下一篇进行详解。
- 线性组合问题
PID控制器往往采用线性组合的方式,然而,对于不同的被控对象,线性组合并不一定是最佳组合方式,往往通过选用不同的非线性函数替代经典的线性组合方式,以求达到更优的控制品质。
- 误差信号跳变问题
尽管反馈信号往往不存在跳变的情况,但给定信号却无法避免跳变。同时,误差信号的计算通过作差得到,这导致了误差信号也是存在跳变现象的。
由于执行机构无法瞬间响应跳变误差信号,对于某些被控对象而言,跳变的误差信号相当于一次极大的冲击,对于被控对象而言不利。因此,我们需要对误差信号进行处理,避免控制器直接对跳变信号进行反馈,这里往往通过安排过渡过程的方式解决该问题,具体的原理将在下篇进行阐述。
总结
PID控制算法作为经典控制理论的标杆算法,至今依然被广泛应用于各个工程领域,相信未来依然会是应用最广泛的控制算法之一。本篇对PID控制算法原理及其主要存在的问题进行了阐述,对于PID控制算法的改进方法,将在下一篇中详细展开。
作者简介: 一个被Coding耽误的无人机算法工程师,控制、导航略懂一二,热衷技术,喜欢乒乓、音乐、电影,欢迎交流。
知乎: @遥远的乌托邦
GitHub: https://github.com/DistantUtopia

