LeetCode：1579.保证图可完全遍历——困难

题目：
1579.保证图可完全遍历
Alice 和 Bob 共有一个无向图，其中包含 n 个节点和 3 种类型的边：

• 类型 1：只能由 Alice 遍历。
• 类型 2：只能由 Bob 遍历。
• 类型 3：Alice 和 Bob 都可以遍历。
  给你一个数组 edges ，其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下，找出可以删除的最大边数。如果从任何节点开始，Alice 和 Bob 都可以到达所有其他节点，则认为图是可以完全遍历的。

返回可以删除的最大边数，如果 Alice 和 Bob 无法完全遍历图，则返回 -1 。

示例 1：

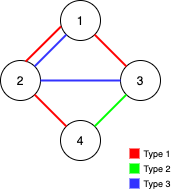
输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出：2
解释：如果删除 [1,1,2] 和 [1,1,3] 这两条边，Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。

示例 2：

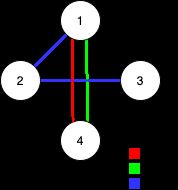
输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出：0
解释：注意，删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。

示例 3：

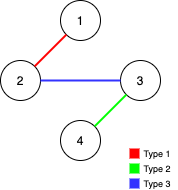
输入：n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出：-1
解释：在当前图中，Alice 无法从其他节点到达节点 4 。类似地，Bob 也不能达到节点 1 。因此，图无法完全遍历。

提示：

• 1 <= n <= 10^5
• 1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
• edges[i].length == 3
• 1 <= edges[i][0] <= 3
• 1 <= edges[i][1] < edges[i][2] <= n
• 所有元组 (typei, ui, vi) 互不相同

解题思路：
先写一个并查集的模板，然后用UF1表示Alice可完成遍历的边，用UF2表示Bob可完成遍历的边。如果Alice 或者 Bob无法完全遍历图，返回-1。利用for循环完成三次遍历，第一次判断公共边是否有多余的，若有则删除；第二次判断类型1的边是否有多余的；第三次判断类型2的边是否有多余的。

代码：

class WeightedQuickUnionUF:
    def __init__(self, n):
        self.parent = [i for i in range(n)]  # parent[i] = parent of i
        self.size = [1 for _ in range(n)]  # size[i] = number of elements in subtree rooted at i
        self.count = n  # number of components

    def component(self):
        '''

        :return: the number of sets
        '''
        return self.count

    def find(self, p):
        '''

        :param p: an element
        :return: the canonical element of the set containing. p所在分量的标识符
        '''
        assert 0 <= p < len(self.parent)
        while p != self.parent[p]:
            p = self.parent[p]
        return p

    def isConnected(self, p, q):
        '''

        :param p: one element
        :param q: the other element
        :return: true if the two element are in the same set.
        '''
        return self.find(p) == self.find(q)

    def union(self, p, q):
        '''
        Merges the set containing element p with the set containing element q.
        :param p: one element
        :param q: the other element
        :return: None
        '''
        rootP = self.find(p)
        rootQ = self.find(q)
        if rootP == rootQ:
            return

        # make samller root point to larger one
        if self.size[rootP] < self.size[rootQ]:
            self.parent[rootP] = rootQ
            self.size[rootQ] += self.size[rootP]
        else:
            self.parent[rootQ] = rootP
            self.size[rootP] += self.size[rootQ]
        self.count -= 1
class Solution:
    def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:
        UF1 = WeightedQuickUnionUF(n+1)
        UF2 = WeightedQuickUnionUF(n+1)
        result = 0

        for edge in edges:
            if edge[0] == 3:
                if UF1.isConnected(edge[1], edge[2]):
                    result += 1
                else:
                    UF1.union(edge[1], edge[2])
                    UF2.union(edge[1], edge[2])
        
        for edge in edges:
            if edge[0] == 1:
                if UF1.isConnected(edge[1], edge[2]):
                    result += 1
                else:
                    UF1.union(edge[1], edge[2])
        
        for edge in edges:
            if edge[0] == 2:
                if UF2.isConnected(edge[1], edge[2]):
                    result += 1
                else:
                    UF2.union(edge[1], edge[2])
        
        if UF1.component() > 2 or UF2.component() > 2:
            return -1
        return result

提交记录：