LDA总结与实例分析
LDA总结与实例分析
- LDA简介
- LDA计算过程
-
- 符号铺垫
- 求解过程
- LDA实例分析
- LDA优缺点
最近AI导论老师介绍了线性判别分析,但是由于板书全英文加上老师讲课过快,课上我没能完全理解LDA的原理。课下做了很多功课,才初步对LDA有了一个认识。下面我按照老师的板书流程并添加注释来讲述LDA求解全过程。
LDA简介
LDA全称Linear Discriminant Analysis,意为线性判别分析,是一种高效准确的降维方法(只降一维,不精确才难)。简单来说,就是找到一个比原数据集低一维的分类面,让原数据集在此面上投影,投影的结果就是降一维后的新数据集。所以这个面的方向非常重要,它决定了降维后数据的特征保留程度。而我们的LDA求解,就是在研究如何能找到最理想的投影方向。
拿二维数据为例,我们假设有两个大类,分别用蓝色、绿色表示
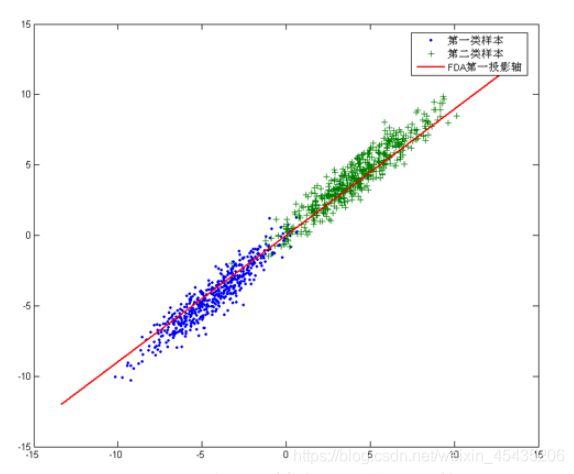
红线即为投影面(超平面),可以想象到,当原数据集中的点向红线投影后,所剩下的信息就只有在红线上的相对位置了,所以我们可以用一维的数据来表示投影后的数据信息。
下面我们在理解如何降维的基础上再看投影面方向的影响
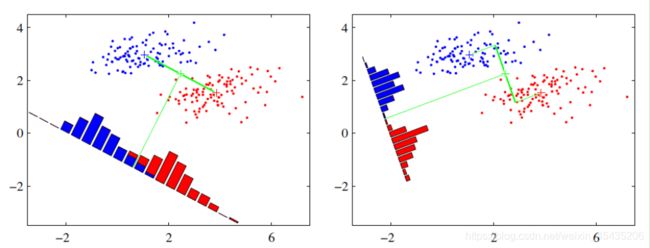
左右两个图同样是二维数据对一维的降维,不同的是,它们的投影超平面方向不相同。不同的投影面让它们降维后数据的离散程度不同。从直观上可以看出,右图要比左图的投影效果好,因为右图的红色数据和蓝色数据各个较为集中,且类别之间的距离明显。左图则在边界处数据混杂。
LDA计算过程
符号铺垫
先对下文要出现的各种符号来一个定义全家福(没有这些铺垫鬼知道老师上课讲的是什么)
所有样本数据一共为两类,1类和2类。
w为待求投影面方向, m 1 m_1 m1、 m 2 m_2 m2为第1类第2类数据的均值,也可以说成原始中心:
m i = 1 N i ∑ x ∈ X i x ( i = 0 , 1 ) m_i = \frac{1}{N_i}\sum\limits_{x \in X_i}x\;\;(i=0,1) mi=Ni1x∈Xi∑x(i=0,1)
类别i投影后的中心点为:
![]()
衡量类别i投影后,类别点之间的分散程度(方差)为:
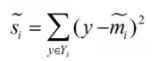
求解过程
投影面的定义为
![]()
求解W就是LDA的任务。我们想找的投影面其实就是让“同一类内的数据点更加聚集,不同类的数据点更加分散”的平面。所以由此我们得出
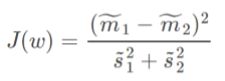
J ( w ) J(w) J(w)可以衡量类内、类外的数据离散程度,使 J ( w ) J(w) J(w)分子最大,分母最小,此时的w就是我们想要的方向。换句话,我们要做的就是最大化 J ( w ) J(w) J(w)
由于 J ( w ) J(w) J(w)此时形式过于紧凑,我们无法直接求出w,所以我们定义 S b S_b Sb, S w S_w Sw,为类间散度、类内散度,对 J ( w ) J(w) J(w)做进一步变换:
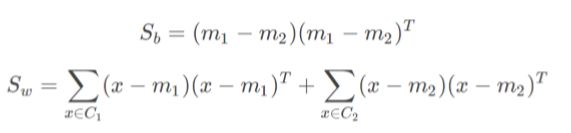
变换后的 J ( w ) J(w) J(w)变为:
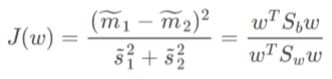
这样,我们就能直观地看到w对函数的影响了
进一步,根据拉格朗日乘数:
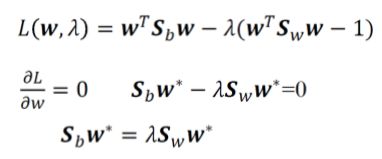
再逆变换得:
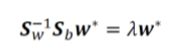
至此,我们就可以求出w了
之后再选取最大特征值对应的特征向量作为投影方向即可
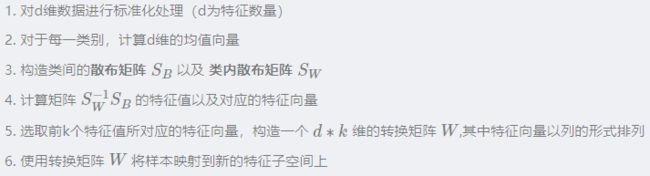
综上所述,LDA可以分为以下6个步骤
LDA实例分析
题目:
• Compute the projection direction using LDA from two sets of points (on the paper by hand)
C1=[(1, 0), (1, 1), (0, 1)]
C2=[(1, 2), (2, 1), (2, 2)]
这是一个二维数据二分类求解问题,数据量不大,我们以这个例子来应用一遍上述的LDA求解过程
第一类中心: m 1 m_1 m1= ( 2 / 3 2 / 3 ) \begin{pmatrix} 2/3 \\2/3\end{pmatrix} (2/32/3)
第二类中心: m 1 m_1 m1= ( 5 / 3 5 / 3 ) \begin{pmatrix} 5/3 \\ 5/3 \\ \end{pmatrix} (5/35/3)
类间散度: S b S_b Sb=( m 1 m_1 m1- m 2 m_2 m2) ( ( ( m 1 m_1 m1 − - − m 2 m_2 m2 ) T )^T )T= ( 1 1 1 1 ) \begin{pmatrix} 1&1 \\ 1&1 \\ \end{pmatrix} (1111)
类内散度: S w S_w Sw= ∑ \sum ∑(x- m 1 m_1 m1) ( x − (x- (x− m 1 m_1 m1 ) T )^T )T+ ∑ \sum ∑(x- m 2 m_2 m2) ( x − (x- (x− m 2 m_2 m2 ) T )^T )T= ( 4 / 3 − 2 / 3 − 2 / 3 4 / 3 ) \begin{pmatrix} 4/3&-2/3 \\ -2/3&4/3 \\ \end{pmatrix} (4/3−2/3−2/34/3)
由 S b S_b Sb、 S w S_w Sw可以求解 S w − 1 S_w^{-1} Sw−1 S b S_b Sbw= λ \lambda λw
先计算 S w − 1 S_w^{-1} Sw−1 S b S_b Sb: S w − 1 S_w^{-1} Sw−1 S b S_b Sb= ( 1.5 1.5 1.5 1.5 ) \begin{pmatrix} 1.5&1.5 \\ 1.5&1.5 \\ \end{pmatrix} (1.51.51.51.5)
S w − 1 S_w^{-1} Sw−1 S b S_b Sb特征值为: λ 1 \lambda_1 λ1=0 λ 2 \lambda_2 λ2=3
对应特征向量:
η 1 \eta_1 η1= ( 1 − 1 ) \begin{pmatrix} 1 \\ -1 \\ \end{pmatrix} (1−1)
η 2 \eta_2 η2= ( 1 1 ) \begin{pmatrix} 1 \\ 1 \\ \end{pmatrix} (11)
因为求 J ( w ) J(w) J(w)的最大值,所以取特征值 λ 2 \lambda_2 λ2=3
此时对应特征向量: η 2 \eta_2 η2= ( 1 1 ) \begin{pmatrix} 1 \\ 1 \\ \end{pmatrix} (11)
所以w= ( 1 1 ) \begin{pmatrix} 1 \\ 1 \\ \end{pmatrix} (11)即为投影方向
LDA优缺点
优点:
(1) 计算速度快
(2) 充分利用了先验知识
缺点:
(1) 当数据不是高斯分布时候,效果不好,PCA也是。
(2) 降维之后的维数最多为类别数-1。
(降维之后的维数最多为类别数-1。所以当数据维度很高,但是类别数少的时候,算法并不适用)
困死了,还差个总结,明天再更。本来想着很快写完,结果对LaTeX 数学公式的语法一窍不通,鼓捣了半天才写出来公式orz