1631 最小体力消耗路径(dfs + 二分查找优化)
1. 问题描述:
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费体力最小的一条路径。
一条路径耗费的体力值是路径上相邻格子之间高度差绝对值的最大值决定的。
请你返回从左上角走到右下角的最小体力消耗值 。
示例 1:
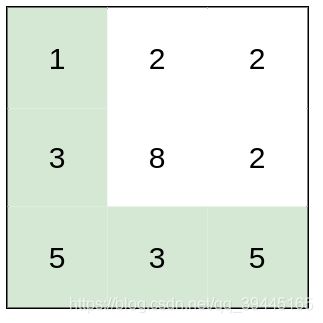
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路劲差值最大值为 3
示例 2:
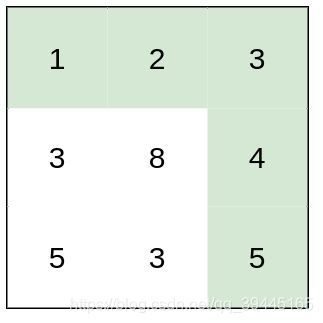
输入:heights = [[1,2,3],[3,8,4],[5,3,5]]
输出:1
解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。
示例 3:
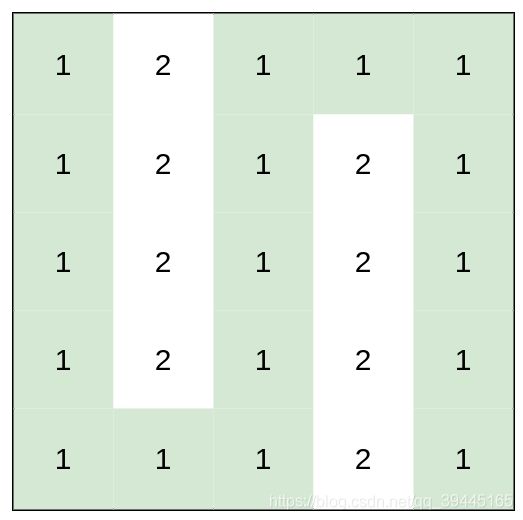
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出:0
解释:上图所示路径不需要消耗任何体力。
提示:
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 106
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/path-with-minimum-effort
2. 思路分析:
① 分析题目可以知道我们需要找到一个能够从起点到达终点的路径,并且这条路径是耗费体力最小的路径,每条路径耗费的体力为这条路径相邻格子之间的高度差绝对值的最大值决定,由此可知这是一道路径搜索问题,我们需要找到一条从起点到达终点的路径并且在搜索路径的时候满足题目的限制条件即可,对于这一类搜索路径的问题,典型的做法是dfs,因为dfs可以搜索所有的路径在找出所有的可能的路径返回最佳的那条路径,一开始的时候使用朴素的dfs去搜索所有的路径(直接从起点搜索到达终点的路径),但是提交上去超时了
② 因为dfs往上下四个方向进行搜索,而且有的矩阵数据规模可能是非常大的,涉及到很多的路径,而且对于当前的四个位置面临着四个方向的判断所以搜索完所有的路径之后肯定会超时,在力扣的题解中的大佬中提供了dfs + 二分查找的思路,看了之后发现思路是真的棒,对于dfs搜索来说真的优化了很多dfs而且并没有搜索所有的路径:有返回值的方法找到一条路径之后就返回True,下面是我对于dfs + 二分查找思路的理解
③ 因为题目给出了heights数组的元素值的范围,所以题目的答案也是在这个范围之中的,所以我们可以通过二分查找的中间距离来搜索矩阵中是否存在从起点到达终点的路径,一开始l = 0, r = 10 ^ 6, mid = (l + r) / 2,我们可以写一个有返回值的dfs方法(有返回值的dfs方法可以避免搜索到满足条件的路径之后再搜索其他的路径),当发现矩阵中存在起点到终点并且路径小于等于mid的时候那么直接返回True,这样可以避免搜索其他的路径(找到一条路径就直接返回True,这样在递归的时候退回到上一层的时候也会返回True层层返回True之后就不会搜索其他的路径了),当我们在二分查找的时候发现距离为mid的时候矩阵中是存在这样的路径的那么说明我们应该缩小右边界r寻找可能更短的距离,否则增大左边界
④ 在dfs方法中,我们可以传递一个二维列表来标记访问过的位置,并且我们在递归方法的一开始就标记当前的位置已被访问,而且在递归退回到上一层的时候是不需要进行回溯的,因为我们是在往下递归的时候有一个限制条件是下一个位置与当前的位置的距离是小于等于mid,所以当我们退回到这一层发现所有小于等于mid距离的位置都被标记了,这个时候肯定是不存在这样一条距离小于等于mid从起点到达终点的路径的,因为假如从当前位置到达标记的位置说明标记的这个位置搜索下去肯定是不符合条件的所以没有必要进行搜索了
⑤ 大佬的题解网址如下:
https://leetcode-cn.com/problems/path-with-minimum-effort/solution/dfs-er-fen-cha-zhao-mo-ban-ti-by-kobe24o/
对于二分查找思路还有如下的题目(盗取大佬的一张图),多做一下类似的题目对于这一类的题目可能更熟悉一点
3. 代码如下:
from typing import List
class Solution:
def dfs(self, heights: List[List[int]], x: int, y: int, pos: List[List[int]], vis: List[List[int]], d: int):
if x == len(heights) - 1 and y == len(heights[0]) - 1:
return True
vis[x][y] = 1
for i in range(4):
x1 = x + pos[i][0]
y1 = y + pos[i][1]
# 这里不用进行回溯因为按照距离小于等于d往下进行递归的假如退回到当前这一层之后发现能够到达的距离小于等于d的位置都被标记了说明是距离小于等于d是不能够从起点到达终点的
if 0 <= x1 < len(heights) and 0 <= y1 < len(heights[0]) and vis[x1][y1] == 0 and abs(heights[x][y] - heights[x1][y1]) <= d:
# 发现存在这样一条距离小于等于d从起点到达终点的路径返回True
if self.dfs(heights, x1, y1, pos, vis, d): return True
# 尝试完当前位置的所有位置之后都没有发现这样一条路径返回False
return False
def minimumEffortPath(self, heights: List[List[int]]) -> int:
pos = [[0, 1], [0, -1], [1, 0], [-1, 0]]
l, r = 0, 10 ** 6
res = 0
while l <= r:
mid = (l + r) // 2
vis = [[0] * len(heights[0]) for i in range(len(heights))]
if self.dfs(heights, 0, 0, pos, vis, mid):
res = mid
r = mid - 1
else:
l = mid + 1
return res