从RNN到LSTM代码实战

RNN

对RNN的简单介绍

RNN的英文全称是Recurrent Neural Network，中文名称是循环神经网络。RNN适用于处理“序列问题”，所谓“序列问题”是指一个样本的特征与特征之间存在明显的先后顺序关系，如对于一张图片，组成该图片的特征是像素，像素与像素之间是有着十分明显的位置排列的关系，因此一个图片的像素组成了一个序列。当我们需要将图片作为输入到模型当中去判断该图片是狗还是猫的时候，这个问题就是“序列问题”。但更为人所熟知的“序列问题”则是与文本相关的问题，单词是文本组成的基本元素，单词与单词之间有明显的先后位置关系。因此，文本分类、文本预测等问题都可以归类为“序列问题”。RNN在处理“序列问题”时有明显的优势，因为它将序列当中元素之间的关系以信息的方式提取出来，并反作用于序列当中元素的处理过程，我们的文本在经过RNN的处理所提炼出的信息自然是更加合理。(白话：我讲的的确有些抽象，我常常用看书的例子来比喻RNN、LSTM的工作机制。RNN在看书的时候，当他看到一个单词，他会用前面所看到的内容来综合理解这个单词的含义，这样去看书，自然能够获得更好的效果。)

那么，在RNN诞生之前，我们是如何来处理序列问题的呢？对于一些简单的机器学习的方法，像逻辑回归、SVM等，它们把序列当中元素的相互关系全部给丢弃了，样本的特征是什么就是什么，它们不会去根据特征之间的关系来对特征进行延申。(白话：我讲得还是挺抽象的，如果你学习过这两种基本的方法的话，也许还能理解得比较到位。举个不太恰当的例子，当你喜欢的女生和你讲no，像逻辑回归、SVM这种傻瓜，会直接认为自己被拒绝掉了。但是RNN、LSTM就很聪明，它会把女生和它讲的话结合起来去看no这个单词，no也需并不代表着拒绝。)。对于MLP(多层感知机)而言，则是过度地考虑了一个元素所代表的涵义，它会结合所有的元素，一起来对这个元素进行分析，从而得到一个新的元素。这种方式太过于笨重，一个序列可能有很多元素，我们的参数实在是太多了，训练该模型会十分缓慢。而RNN、LSTM则是非常轻便，参数量非常少，所以RNN、LSTM是处理“序列问题”时的最佳人选。

带你了解RNN的结构

RNN的宏观作用

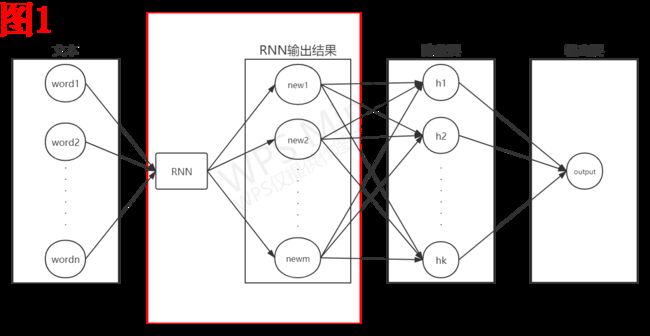
如图1所示，我没有像很多教程当中那样，不关注RNN在一个完整的系统当中所处的位置，直接去分析RNN内部的结构，这对于新手而言是很不友好的。我是将RNN在一个完整系统当中所处的位置给大家先展示出来，希望以一种由宏观到微观的过程来给大家介绍RNN。如图1所示，这是一个完整的文本二分类的模型架构(我把文本预处理的部分去除了)，我们在代码实战当中，使用的就是这样一个模型架构。RNN自身并不是一个完整的模型，它自己什么也干不了，它的作用是对我们输入的文本进行加工处理，我们使用RNN加工处理之后的结果来代替原本的文本数据进行分类。(白话：对于RNN，你必须要建立起一个宏观的概念，它只是一个完整模型当中的一个组件而已。就像是汽车的发动机一样，它只是汽车的一个重要的组成部分。单靠发动机，什么也做不了。)

我来给大家描述一下图1的大致过程，我们希望输入一个文本到模型当中之后，可以得到关于该文本是正向情感文本还是负向情感文本的判断结果。输入的文本数据包含有n个单词，我们就以这n个单词作为该文本的各个维度的特征。我们将该n*d的矩阵T输入到RNN当中，d为词向量的维度，我们先不去关心RNN内部是如何处理T的。RNN输出的是一个m维的向量R，我们使用该m维的向量R输入到全连接隐藏层当中，得到了k维的隐藏层向量H。最后，我们使用仅包含一个单元的输出层，使用sigmoid来作为激活函数，输出值靠近0为负样本，靠近1为正样本。

RNN内部的结构

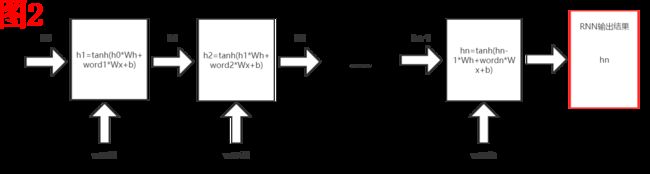
如图2所示，就是RNN在处理文本时的具体过程。会有一些数学上的计算，做好准备，不过不会太难。我们首先看一下图2的整体结构，它是一个从左到右的基本结构。对于文本当中的n个单词，我们进行了从左到右一共n步计算，最后得到了RNN处理的输出结果hn。

让我们来细致地描述一遍图2吧，h这个向量实际上代表着我们的记忆，让我们先把目光聚焦到第一个小方块单元上。此时我们的记忆h0是空白的(0向量)，因为我们还没有处理这个文本当中的任何一个单词。word1是文本的第一个单词向量，它与记忆h0一同输入到第一个小方块当中，完成了一个运算去获取关于第一个单词的记忆h1。之后，我们又将带着这份记忆h1去处理第二个单词向量word2。到了最后一步，我所获得的hn，它代表着我们对于这个文本整体的记忆。因此，我们将hn作为RNN处理的输出结果。

那么，对于小方块当中的计算是如何进行的呢？
$$h1=tanh(h_0\ast W_h+wor{d}_1\ast W_x+b)$$
在这个式子当中，h的维度是RNN的一个超参数，我们可以人为去指定。我们就假定h的维度为m维，而对于$W_h$，它是一个矩阵，矩阵的维度为$m\ast m$，它是RNN的一项参数，通过反向传播来进行调节优化，$W_h$的初值我们通常使用正态分布来生成。还记得线性代数的一点内容的话，我们应该很容易能够知道$h_0\ast W_h$的结果仍旧是一个m维的向量。而$wor{d}_1$是一个d维的词向量，$wor{d}_1\ast W_x$的结果也一定是一个m维向量，因为它要和$h_0\ast W_h$相加，向量之间相加必须要尺寸一致。所以，$W_x$是一个尺寸为$d\ast m$的矩阵，它同样是RNN的参数，要进行反向传播调节优化。$b$是我们常常所说得偏置项，它是维度为m的向量，初值一般设为全0。

至于RNN所使用的激活函数$tanh$，以我的经验来理解$tanh$的话，它常常用于提取信息的时候。相比于sigmoid函数，它不仅能起到$sigmoid$所具备的归一化的效果，还能够保持数据的正负号，在进行信息表示时，$tanh$函数的表达能力更强。
$$\begin{gathered} tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} \\ sigmoid(x)=\frac{1}{1+e^{-x}} \end{gathered}$$

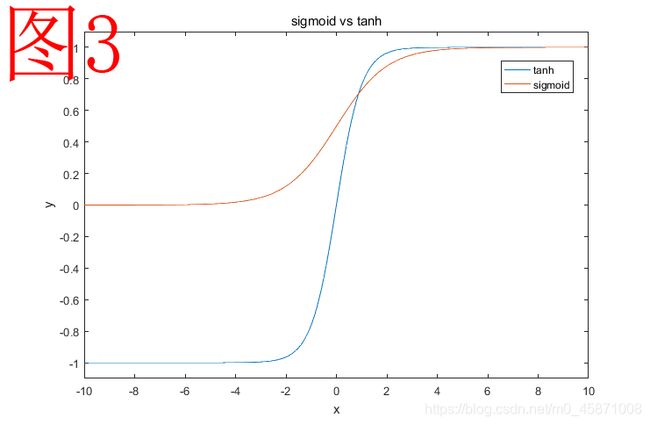
我们从图3进行观察的话，最为直观的感受就是$tanh$和$sigmoid$的值域不一样。值域不同到底会有什么样的影响？没事儿躺在床上可以想一想。

RNN代码实战

任务介绍

做RNN的实战任务，使用文本分类是作为合适不过了。我所选用的数据集是IMDB(豆瓣)影评数据集，数据集当中包含有24500份数据，它们一部分是正向情感的影评数据，另一部分是负向情感的影评数据。我将这24500份数据中的17000份作为训练数据，7500份作为测试数据。我们的目标就是希望尽可能地去将这7500份数据都去预测准确。
数据集下载链接

编程环境设置

• Python3.5
• Tensorflow1.8.0

因为我是使用tensorflow1.8.0这个框架来搭建RNN的，python的版本下调至3.5。(很多同学做研究使用的是pytorch，基本原理是差不多的。)

代码详细解析

数据读取

import math
import re
import keras
import numpy as np
import pandas as pd
import tensorflow as tf
from keras.preprocessing.text import Tokenizer
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
#读取数据
train = pd.read_csv('train_17000.tsv', sep='\t')#训练集数据
test = pd.read_csv('test_7500.tsv', sep='\t')#测试集数据
train_data = train.loc[:, 'data']#训练集数据的'data'字段
train_labels = train.loc[:, 'labels']#训练集数据的'label'字段
test_data = test.loc[:, 'data']#测试集的'data'字段
test_labels = test.loc[:, 'labels']#测试集'label'字段

IMDB数据是以tsv文件格式保存的，tsv这种格式特别适合于机器学习数据的保存，我们可以通过属性名称去访问到一条样本数据的某个属性值。我们通过读取数据，就将训练集数据保存在了变量train当中，将测试集数据保存在变量test当中。我之所以要将数据和标签(label)分成两部分，是为了对数据部分进行预处理时会比较方便。

文本数据预处理

print(train_data.loc[0])

打印结果：

我们来打印一下训练数据来观察一下，我们当前的数据还是文本内容。但是，如果我们要让机器学习算法来处理的话，我们必须要将文本转化成维度一致的“数字向量”才可以。

# RNN 需要的参数
def get_default_params():
    return tf.contrib.training.HParams(
        num_embedding_size=16,  # 词向量的维度
        num_timesteps=50,  # 时间步的长度
        max_len=50,  # 文本的单词数目，注意它要与num_timesteps的值保持相同
        vocab_size=6000,  # 单词->数值表示时的词典大小。单词种数超过6000将转化成0进行表示。
        num_rnn_nodes=32,  # Rnn模块的维度
        num_fc_nodes=32,  # Rnn处理完之后，使用全连接层来进行后续处理
        batch_size=500,  # 一个batch所处理的样本数目
        clip_lstm_grads=1.0,  # 当梯度计算超过1时，令其为1
        learning_rate=0.001,  # 学习速率
        num_word_threshold=10,  # 过滤掉词频太少的单词，我们不会将这类单词转化为数值表示，而是直接化为0.10是在整个训练集当中统计的结果
    )
hps = get_default_params()  # 我们通过hps来调用相应的参数来进行使用

# 数据的预处理
def clear_review(text):
    texts = []
    for item in text:
        item = item.replace("

", "")
        item = re.sub("[^a-zA-Z]", " ", item.lower())
        texts.append(" ".join(item.split()))
    return texts


# 删除停用词+词形还原
def stemed_words(text):
    stop_words = stopwords.words("english")
    lemma = WordNetLemmatizer()
    texts = []
    for item in text:
        words = [lemma.lemmatize(w, pos='v') for w in item.split() if w not in stop_words]
        texts.append(" ".join(words))
    return texts


# 文本预处理
def preprocess(text):
    text = clear_review(text)
    text = stemed_words(text)
    return text


train_data_prc = preprocess(train_data)  # 训练数据进行预处理
t = Tokenizer(num_words=hps.vocab_size)  # Tokenizer对象负责将单词转化为数值表示的结果，我们可以指定单词的数目
t.fit_on_texts(train_data_prc)  # t阅读我们预处理完之后文本数据，建立起单词到数值表示的映射关系
new_train_data = t.texts_to_sequences(train_data_prc)  # 将预处理后的文本转化为数值表示的结果，单词用数值[0,6000]进行表示。
new_train_sequence = keras.preprocessing.sequence.pad_sequences(
    new_train_data, maxlen=hps.max_len, padding='post', truncating='post'
)  # 我们的每一个文本，在转化为数值表示的结果后，每一条文本的数值数量也应当修剪为一样的长度。机器学习是不会接受数据的维度是变化不一的

# 对于测试集数据，我们进行同样的处理
test_data_prc = preprocess(test_data)
new_test_data = t.texts_to_sequences(test_data_prc)
new_test_sequence = keras.preprocessing.sequence.pad_sequences(new_test_data, maxlen=hps.max_len
                                                               , padding='post', truncating='post')

# 我们将处理完的数据的维度进行调整到适合训练所要求的维度
new_test_sequence = new_test_sequence.reshape(-1, hps.max_len)
np_train_labels = np.array(train_labels)
np_train_labels = np_train_labels.reshape(-1, 1)
new_test_labels = np.array(test_labels)
new_test_labels = new_test_labels.reshape(-1, 1)

# 分别将训练集和测试集的数据的标签与数据部分合并起来
new_train = np.concatenate((np_train_labels, new_train_sequence), axis=1)
new_test = np.concatenate((new_test_labels, new_test_sequence), axis=1)

对于文本数据，我们进行的预处理工作包括将单词的大小写转化为小写，将一些停用词表当中的单词去除掉(停用词是指一些对于文本分类无关紧要的单词，比如am is that之类的单词)。接着，我们使用数字来替换单词，并压缩成相同的维度的数据向量。在这段代码当中，我们调用了一些库包来辅助我们完成一些预处理工作。如Tokenizer是用来将单词替换成数字的，keras.preprocessing.sequence.pad_sequences()函数则是帮助我们将替换成数字后的数据向量，压缩成维度一致的向量。get_default_params()函数负责提供我们需要的一些参数，我们通过hps来调用相应的参数。

让我们尝试打印一下文本数据被转化成了什么样子。

print(new_train[0,1:])

打印结果：

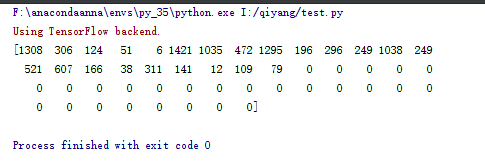
我们将每一个样本的文本数据转化成了维度为50维的数字化的向量，至此，我们就可以进行下一步，将转化为数字向量的文本数据交给我们的模型来进行处理了。这也是RNN编程最核心的部分。其实，对于文本数据的预处理，我们还不算完全做完了，现在，我们只是用一个数字来表示一个单词，但是我们更希望用一个词向量表示一个单词。我们后续还会继续处理，我们最终将得到[sample_num,word_num,word_dimension]这样的三维矩阵。

• sample_num:样本的数目，训练集有17000个样本，测试集有7500个样本。
• word_num:一个样本当中所包含的单词数目(一致的单词数目)
• word_dimension:词向量的维度

RNN模块设计

import  tensorflow as tf
import math

class RNN_last():
    def __init__(self, word_dms, ln_nodes, name):
        '''
            :param word_dms:输入的词向量的维度
            :param ln_nodes: RNN内部的向量的维度
            '''
        self.__word_dms = word_dms
        self.__ln_nodes = ln_nodes
        scale = 1.0 / math.sqrt(self.__word_dms + self.__ln_nodes) / 3.0
        RNN_init = tf.random_uniform_initializer(-scale, scale)
        with tf.variable_scope(name + '_RNN_moudel', initializer=RNN_init):
                self.__Wx, self.__Wh, self.__b = self.__generate_parameters()


    def __generate_parameters(self):
        '''
        产生Wx,Wh,bias参数
        :return:
        '''
        Wx = tf.get_variable('weights_x', [self.__word_dms, self.__ln_nodes])
        Wh = tf.get_variable('weights_h', [self.__ln_nodes, self.__ln_nodes])
        bias = tf.get_variable('bias', [1, self.__ln_nodes], initializer=tf.constant_initializer(0.0))
        return Wx, Wh, bias

    def calculate(self, input_data):
          '''
          :param input_data:RNN模块要去处理的数据，它的维度为[batch_size,num_words,dms_word]
          :return:h,将最后一步的h作为输出
          '''
          #h为
          h = tf.Variable(tf.zeros([input_data.shape[0],self.__ln_nodes]),trainable=False)

          #对每个时间步进行计算
          for i in range(input_data.shape[1]):
               #将i时间步处的词向量提取出来，完成后续的计算
               vector = tf.reshape(input_data[:,i,:],[input_data.shape[0],input_data.shape[2]])
               h = tf.nn.tanh(
                   tf.matmul(vector,self.__Wx)+tf.matmul(h,self.__Wh)+self.__b
               )
          return h

• batch_num:投入训练的样本的数目。
• word_num:一个样本当中所包含的单词数目(一致的单词数目)
• word_dimension:词向量的维度

我将RNN模块单独写成了一个类，这样比较方便大家来进行分析。这段代码整体还是比较简单的，但是想把这段代码读得很清楚，需要对tensorflow1.x的版本比较清楚，可以自己尝试写一个简单的逻辑回归的实验练一练。我相信各位一定是对calculate函数当中的内容非常感兴趣，我认为还是有必要做一个详细的说明。对于h而言，我们将其声明为尺寸为[batch_num,ln_nodes]的矩阵，我们要对这batch_num条数据进行RNN的处理。我们再一下calculate函数当中的循环，input_data.shape[1]对应的是word_num，我们要对样本当中的每一个单词进行遍历分析，input_data[:,i,:]就是我们所提取到的单词，它的维度为[batch_num,1,word_dimension]。但是，tensorflow要求矩阵乘法运算只限于二维矩阵，所以我们要将其reshape成[batch_num,word_dimension]的矩阵。剩下的就没有难以理解的地方了。

计算流图的搭建

之前，我们也已经提到了，RNN只是整个系统的一部分，一个处理模块儿而已。我们现在需要把数据进入系统进行处理的完整流程给大家展现出来。我是用一个函数来将这个系统给封装了起来。我建议你先对照着图1去理解这部分代码。

from Qiyang_TEXT.Layers import RNN_last
rnn = RNN_last(hps.num_embedding_size, hps.num_rnn_nodes, 'Rnn_moudel')#建立RNN模块处理对象
def create_model(hps, vocab_size, num_classes):
    '''
    构建lstm
    :param hps: 参数对象
    :param vocab_size:  词表 长度
    :param num_classes:  分类数目
    :return:
    '''
    num_timesteps = hps.num_timesteps  # 一个句子中 有 num_timesteps 个词语
    batch_size = hps.batch_size  # 一个epoch参与训练的数据样本的数目

    # 设置两个 placeholder， 内容id 和 标签id
    inputs = tf.placeholder(tf.int32, (batch_size, num_timesteps))  # 每个epoch抽象的输入数据
    outputs = tf.placeholder(tf.int32, (batch_size,))  # 每个epoch的抽象数据所对应的标签值

    global_step = tf.Variable(
        tf.zeros([], tf.int64),
        name='global_step',
        trainable=False)  # 用于保存当前训练的步数

    # 数据初始化，我们使用-1到1之间的均匀分布来产生数据
    embeding_initializer = tf.random_uniform_initializer(-1.0, 1.0)

    with tf.variable_scope('embedding', initializer=embeding_initializer):
        # 负责将数据当中的数值所表示的单词，扩展为用一个词向量来进行表示
        embeddings = tf.get_variable('embedding', [vocab_size, hps.num_embedding_size], tf.float32)

        # inputs的维度为[batch_size,numsteps],而经扩展后得到[batch_size,numsteps,dimension]
        embeding_inputs = tf.nn.embedding_lookup(embeddings, inputs)
    
    outputs = rnn.calculate(embeding_inputs)   

    # 将outputs_p3传入到一个全连接层当中
    fc_init = tf.uniform_unit_scaling_initializer(factor=1.0)
    with tf.variable_scope('fc', initializer=fc_init):  # initializer 此范围内变量的默认初始值

        # 这种全连接层的使用方式非常简便，fc1就是我们得到的在该全连接层的每个单元的激活值
        fc1 = tf.layers.dense(outputs,
                              hps.num_fc_nodes,
                              activation=tf.nn.relu,
                              name='fc1')
        # 为避免过拟合，我们将将某些隐藏层单元给停用掉
        fc1_dropout = tf.nn.dropout(fc1, 0.8)  # 0.8表示我们保留可用的单元的比例

        # 对于输出层，我们只有一个单元，logits表示我们的输出结果[batch_size,1]，因为需要计算loss值，我们暂时不加sigmoid函数
        logits = tf.layers.dense(fc1_dropout,
                                    1,
                               name='fc2')
        logits = tf.reshape(logits, (logits.shape[0],))
        outputs = tf.cast(outputs, tf.float32)

    with tf.name_scope('metrics'):
        binary_loss = tf.nn.sigmoid_cross_entropy_with_logits(
            logits=logits,
            labels=outputs
        )
        loss = tf.reduce_mean(binary_loss)

        # 为计算预测准确率，我们将0到1之间的激活值进行4舍5入，便可得到0、1标签
        y_pred = tf.round(
            tf.nn.sigmoid(logits)
        )

        # 完成准确率的计算
        correct_pred = tf.equal(tf.cast(outputs, tf.int32), tf.cast(y_pred, tf.int32))  # 这里也做了修改
        accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

    with tf.name_scope('train_op'):
        tvars = tf.trainable_variables()  # 获取所有可以训练的变量
        for var in tvars:
            tf.logging.info('variable name: %s' % (var.name))  # 打印出所有可训练变量

        # 对求取的梯度值进行截断操作
        grads, _ = tf.clip_by_global_norm(
            tf.gradients(loss, tvars),  # 计算loss对于各个变量进行反向求导的梯度值
            hps.clip_lstm_grads
        )

        # 计算当前的loss关于输入词的梯度，用它来反映不同位置的单词对于结果的影响力度
        grad_input = tf.gradients(loss, embeding_inputs)
        optimizer = tf.train.AdamOptimizer(hps.learning_rate)  # 对参数进行梯度修改
        train_op = optimizer.apply_gradients(
            zip(grads, tvars),  # 将 梯度和参数 绑定起来
            global_step=global_step
        )
    return ((inputs, outputs),
            (loss, accuracy),
            (train_op, global_step, grad_input))

计算流图是一个非常重要的概念，其中的inputs和outputs就像是训练数据的入口，也可以理解为我们抽象出来的训练数据的占位符，它负责代表实际的数据将完整的计算过程给描述出来，我们要把loss、准确率等一些列重要的信息给求取出来。在优化训练部分，我们将求取到的grads梯度值，应用到所有的可训练变量之上，进行梯度更新。

让计算流图动起来

#建立计算流图，并返回我们需要观察的重要的量
placeholders, metrics, others = create_model(
    hps, hps.vocab_size, 2
)

#输入数据，数据对应的标签
inputs, outputs = placeholders
#loss值，准确率
loss, accuracy = metrics
#优化训练操作对象，当前步数，对输入数据的反向求导值
train_op, global_step, grad_input = others

#在开启计算流图之前必须要执行，建立计算流图当中使用到的变量，让计算流图能够正常运行
init_op = tf.global_variables_initializer()
train_keep_prob_value = 0.8
test_keep_prob_value = 1.0

# 进行10000个epoch的训练
num_train_steps = 10000

# 用于保存训练过程当中的训练结果
gradient_max_save = np.array(np.zeros((1, 50)))
train_accuracy_save = []
test_accuracy_save = []
loss_save = []

#计算测试集数据的结果
def eval_holdout(sess, dataset_for_test, batch_size):
    '''
    该函数的主要功能是用测试集的数据进行测试
    :param sess: 用于调用开启计算流图的对象
    :param dataset_for_test: 测试数据集
    :param batch_size: 选取进行测试的数据的数目
    :return: 将准确率与loss值返回
    '''
    accuracy_vals = []  # 存储记录准确率值
    loss_vals = []  # 存储记录loss值
    for i in range(int(Pa.TEST_DATA_NUM / hps.batch_size)):
        # 我们将该batch的数据的标签和数据给抽取出来
        batch_labels = dataset_for_test[i * hps.batch_size:(i + 1) * hps.batch_size, 0]
        batch_inputs = dataset_for_test[i * hps.batch_size:(i + 1) * hps.batch_size, 1:]
        batch_labels = batch_labels.reshape(-1)

        # 获取准确率、loss值
        accuracy_val, loss_val = sess.run([accuracy, loss],#计算测试集数据时不进行优化
                                          feed_dict={
     
                                              inputs: batch_inputs,
                                              outputs: batch_labels
                                          })

        # 将当前batch的准确率和loss值进行存储记忆
        accuracy_vals.append(accuracy_val)
        loss_vals.append(loss_val)
        # 返回准确率均值、loss均值
    return np.mean(accuracy_vals), np.mean(loss_vals)


with tf.Session() as sess:#开启会话，就在这里启动计算流图
    sess.run(init_op)  # 首先对模型的参数进行初始化
    for i in range(num_train_steps):
        # 随机选择训练集数据当中的一个batch来进行训练
        batch_inputs, batch_labels = random_select_batch(hps.batch_size, new_train)
        batch_labels = batch_labels.reshape(-1)

        # 开启运行计算流图
        outputs_val = sess.run(
            [loss, accuracy, train_op, global_step],
            feed_dict={
     
                inputs: batch_inputs,
                outputs: batch_labels
            }
        )

        # 完成当前epoch的数据记录工作
        loss_val, accuracy_val, _, global_step_val = outputs_val
        gradient_mat = sess.run(grad_input, {
     inputs: batch_inputs, outputs: batch_labels})
        gradient_mat = np.array(gradient_mat)
        gradient_mat = gradient_mat.sum(axis=3)
        gradient_mat = gradient_mat.mean(axis=1)
        loss_save.append(loss_val)
        train_accuracy_save.append(accuracy_val)
        print(i + 1, '次训练!', 'loss:', loss_val, ' accuracy:', accuracy_val)

        # 每100次进行一次测试集数据的运算
        if global_step_val % 100 == 0:
            gradient_max_save = np.concatenate((gradient_max_save, gradient_mat), axis=0)
            testdata_accuracy, testdata_loss = eval_holdout(sess, new_test, hps.batch_size)
            test_accuracy_save.append(testdata_accuracy)
            print('测试!', 'loss:', testdata_loss, ' accuracy:', testdata_accuracy)

让计算流图动起来，其实很简单。这一部分代码的主要工作是我们首先要执行create_model函数，将计算流图先建立好，并且将一些我们希望去观察或者使用的量从中获取出来，方便我们进行保存于观察。然后，我们要从我们的数据集当中抽取数据，在每一次训练当中投入数据到计算流图当中进行运算，每一次训练，模型的参数就会得到优化。
完整示例代码下载

LSTM

LSTM简单介绍

LSTM与RNN其实是很相近的，LSTM就是在RNN的基础上被设计出来的。LSTM相比于RNN而言具有更好的性能，而原因在于LSTM可以保存更加长时间的记忆，让他在处理序列当中的元素的时候，可以使用更加全面的记忆来处理当前的元素，我们处理的结果自然也就更好。(白话：LSTM就像是一个记忆力更强的人去看书，而RNN则是记忆力很差。LSTM每当看到新的内容，他立刻就能回忆起前面几十页之前的某个细节，对新内容的解读可以说是收到擒来。RNN则是看到新内容一头雾水，“乔大侠怎么跑上海了”，RNN根本就理解不了，因为他已经完全忘记前面发生了什么。开个玩笑，总之LSTM和RNN的区别就在于记忆力。)

LSTM的内部结构

LSTM的宏观上的作用与RNN是完全一样的，我就不和大家啰嗦了。

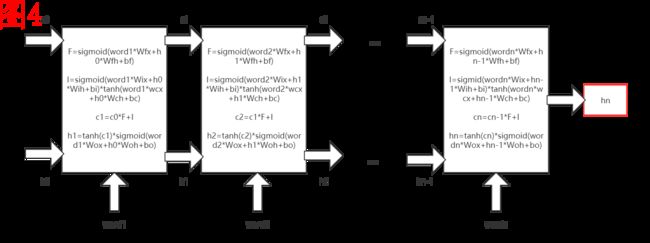
我们先来大致观察一下LSTM的整体结构，它和RNN一样，都是从左到右的基本结构。最后，我们也是以$h_n$来作为LSTM模块的处理的输出结果。我们再仔细观察，会发现LSTM和RNN至少有两个明显不一样的地方，首先，小方块内部的运算更多了，貌似更复杂了。其次，我们不止有h在小方块之间进行传递，而且还有c值在小方块之间进行传递。这两个地方实际上就已经是LSTM和RNN的全部区别了。

我先和大家聊聊c值代表着什么，c值的意义是长期记忆，而h则对应短期记忆。RNN只有短期记忆h，这是由于“梯度消失”所导致的问题。因为，在反向传播的过程当中，在RNN模块当中，是沿着一个很长的序列向前传播，梯度值会不断减小，这就意味着序列当中处于头部的元素对于结果的影响是难以调节的。而我们的c值，沿着这条线来进行反向传播的话，梯度值不会减小得很快，可以有效地克服梯度消失所带来的问题。大家需要很清楚，c值可以作为长期记忆，是因为它有效减缓了梯度消失的问题。那么，为什么用hn而不是cn来作为LSTM的输出结果呢？我们可以看看小方块内部的运算，h值的计算在最后一步完成，c值参与计算得到h值，所以h值作为最后的计算结果，理应作为模型的输出结果。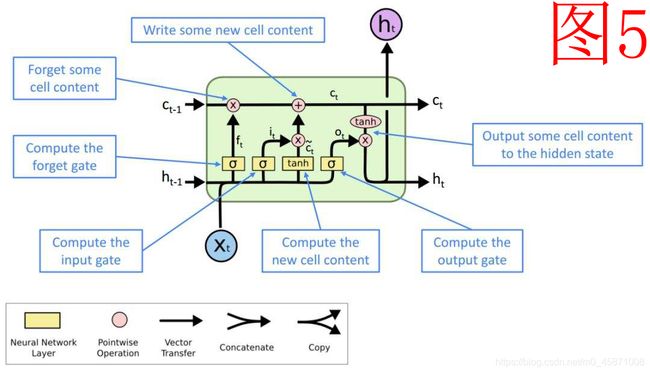
我们用图5来展示一下小方块的内部结构图，我们来仔细分析一下lstm模块当中的细节。

遗忘门

首先，在小方块内部进行的第一步计算称为遗忘门。遗忘门的功能是对长期记忆c值进行缩放，实际上是不可能完全“遗忘”的。我们来看一下遗忘门的计算公式：
$$F=sigmoid(x_t\ast W_{fx}+h_{t-1}\ast W_{fh}+b_f)$$
$sigmoid$函数的值域为(0,1)，是不可能取到0的。$F$当中的值都是属于(0,1)的，所以实际上$F$是要对c值进行缩放，将c中值给缩小了，也可以说是舍弃了一部分，或者遗忘了一部分。(白话：对于“门”实际上是有一丝“过滤”的含义在里面，过这道门，怎么着也得挤掉一些东西。)
$$c_t=c_{t-1}\odot F+\overline{C}$$
$\odot$表示相同尺寸的向量或者矩阵当中的对应位置的元素进行相乘。$\overline{C}$则表示输入到c值当中的输入信息。

输入门

输入门，还是门结构，所以它是要对某个量进行过滤筛除。而这个量就是我们要输入到长期记忆c当中的输入信息$\overline{C}$。
$$I=sigmoid(x_t\ast W_{ix}+h_{t-1}\ast W_{ih}+b_i)$$
我们用得还是$sigmod$函数，凡是门的计算，都是要使用$sigmoid$函数的，这得益于$sigmoid$函数的取值范围恰好是(0,1)处于完全忘记和完全记忆之间。所以最后$\overline{C}$的取值为:
$$\overline{C}=I\odot \overline{C}$$

输入信息

关于输入信息，我们不再是计算门了。所以，在这里我们使用的是$tanh$函数，既起到压缩数据的非线性化的作用，又能够做到对数据的正负号进行保持。保证了信息的原汁原味。
$$\overline{C}=tanh(x_t\ast W_{\overline{c}x}+h_{t-1}\ast W_{\overline{c}h}+b_{\overline{c}})$$
如果你有足够细心的话，你可能会问这样一个问题，为什么$\overline{c}$作为长期记忆没有参与到遗忘门、输入门、输入信息的计算当中呢？h作为短期记忆，都有参与到其中。如果你有这样的问题，说明你已经思考得很深入了。其实，$\overline{c}$是有参与到的，因为$h_{t-1}$的生成是有$c_{t-1}$的参与的。所以短期记忆h，实际上是短期与长期记忆的结合体。

输出门

看到"门"，我们首先想到的就是$sigmoid$函数(有没有形成条件反射？^_^)。
$$O=sigmoid(x_t\ast W_{ox}+h_{t-1}\ast W_{oh}+b_o)$$
输出门控制得是小方块输出的结果，这个结果首先要输入到下一个小方块当中，或者说直接作为LSTM模块输出的一部分为后面的全连接层使用。
$$h_t=tanh(\overline{C})\odot O$$
$h_t$就是这个小方块的输出结果。LSTM有word_num个小方块，我们将最后一个小方块的输出作为LSTM的最终输出结果，并将其交付给后续的全连接层进行处理。

为什么长期记忆C可以去抵抗梯度消失？

我并不打算讲得很深入(我自己其实也是略知一二)，大家更需要的是先明白其中的道理，而不是直接过于专注于细节。我分析所采用的方法是进行对比，我们对比一下RNN当中h的正向变化过程与LSTM当中$\overline{c}$的正向变化过程。h的值的变化是通过h与$W_h$相乘，经tanh函数激活产生一个新的h，然后再经历相乘、激活产生后续的h。我们注意到一个关键词是“相乘”。而在LSTM当中，$\overline{c}$的更新是靠相加，输入信息与c值相加来更新c值。相加和相乘的差别是非常大的，一个数连续乘以一个系数多次，所得的结果就会变得非常小。而相加则不会。
$$c_t=c_{t-1}\odot F+\overline{c}$$
通过加上一项$\overline{c}$来实现c值的稳定性，反向传播的时候，我们靠得是加法。而RNN靠得是乘法，梯度值是越乘越小，而LSTM的梯度值靠加法，则是缓慢变化。我认为这是LSTM能够抵抗梯度消失的非常关键的一点。(白话：我所讲的只是一个大概的思路，LSTM通过引入一个加法项，从而大大减缓了梯度值的变化速率，我们不如来做个小实验观察一下。)

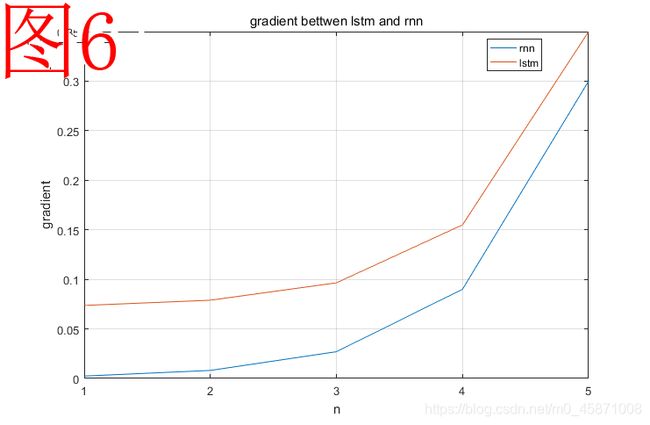
如图6所示，这是我做的一个关于LSTM和RNN的梯度值变化的对比实验。这个实验很简单，我使用两个函数来模拟RNN当中h值的变化，以及LSTM当中c值的变化。当然只是大致进行模拟。实验代码如下，采用matlab2016进行编写。我们不难发现，按照lstm的方式，添加了一个加法项之后，反向的梯度值下降得更加缓慢了，有效解决了梯度消失的问题。
$$\begin{gathered} h=h\ast W_h \\ {c}_t=(c_{t-1}\odot F+b) \end{gathered}$$
我们对于h的变化的模拟，是利用x的幂函数来完成的，用$[x^5,x^4,x^3,x^2,x]$这个序列来表示各个步骤下的梯度值。对于c而言，我们则是添加一个加法项，用$[(((((x+b)x+b)x+b)x+b)x+b)x+b,((((x+b)x+b)x+b)x+b)x+b,(((x+b)x+b)x+b)x+b,((x+b)x+b)x+b,(x+b)x+b,x+b]$来表示LSTM当中各个序列位置下的梯度值。

%matlab 2016
x=0.3;
b=0.05;
n=[1,2,3,4,5];
rnn=x.^n;
lstm=[0,0,0,0,0];
temp=x;
for i=(1:length(n))
    temp=temp+b;
    lstm(i)=temp;
    temp=temp*x;
end
rnn = fliplr(rnn);//序列反向排列
lstm=fliplr(lstm);//序列反向排列
figure(1);
plot(n,rnn);hold on;
plot(n,lstm);
xlabel('n');
ylabel('gradient');
title('gradient bettwen lstm and rnn');
legend('rnn','lstm');
hold off;

LSTM实战代码

对于LSTM的实战代码，我就专门将LSTM模块的代码给大家展示出来。其余文本预处理，全连接层分类，计算流图建立，计算流图启动都和RNN代码实战当中的内容一致。

class LSTM_last():
    def __init__(self,word_dms,ln_nodes,name):
        '''
        :param word_dms:输入的词向量的维度
        :param ln_nodes: LSTM内部的向量的维度
        '''
        self.__word_dms = word_dms
        self.__ln_nodes = ln_nodes
        scale = 1.0 / math.sqrt(self.__word_dms + self.__ln_nodes) / 3.0
        lstm_init = tf.random_uniform_initializer(-scale, scale)
        with tf.variable_scope(name+'_lstm_parameters',initializer=lstm_init):
               #遗忘门的参数
               with tf.variable_scope('forget_gate'):
                       self.__fx,self.__fh,self.__fb = self.__generate_parameters()
               #输入门的参数
               with tf.variable_scope('input_gate'):
                       self.__ix,self.__ih,self.__ib = self.__generate_parameters()
               #输入控制的参数
               with tf.variable_scope('memory'):
                       self.__mx,self.__mh,self.__mb = self.__generate_parameters()
               #输出门的参数
               with tf.variable_scope('output_gate'):
                       self.__ox,self.__oh,self.__ob = self.__generate_parameters()
    def __generate_parameters(self):
        '''
        产生相应的对应于四个门的控制参数的参数
        :return:
        '''
        Wx = tf.get_variable('weights_x',[self.__word_dms,self.__ln_nodes])
        Wh = tf.get_variable('weights_h',[self.__ln_nodes,self.__ln_nodes])
        bias = tf.get_variable('bias',[1,self.__ln_nodes],initializer=tf.constant_initializer(0.0))
        return Wx,Wh,bias
    def calculate(self,input_data):
        '''
        :param input_data:LSTM模块要去处理的数据，它的维度为[batch_size,num_words,dms_word]
        :return:
        '''

        #LSTM模块中间所使用到的变量h,c，负责记忆中间计算的结果
        h = tf.Variable(tf.zeros([input_data.shape[0],self.__ln_nodes]),trainable=False)
        C = tf.Variable(tf.zeros([input_data.shape[0],self.__ln_nodes]),trainable=False)

        #对每个时间步进行计算
        for i in range(input_data.shape[1]):
            #将i时间步处的词向量提取出来，完成后续的计算
            vector = tf.reshape(input_data[:,i,:],[input_data.shape[0],input_data.shape[2]])
            forget_gate = tf.nn.sigmoid(
                tf.matmul(vector,self.__fx)+tf.matmul(h,self.__fh)+self.__fb
            )
            input_gate = tf.nn.sigmoid(
                tf.matmul(vector,self.__ix)+tf.matmul(h,self.__ih)+self.__ib
            )
            memory = tf.nn.tanh(
                tf.matmul(vector,self.__mx)+tf.matmul(h,self.__mh)+self.__mb
            )
            C = tf.multiply(C,forget_gate)+tf.multiply(input_gate,memory)
            output_gate = tf.nn.sigmoid(
                tf.matmul(vector,self.__ox)+tf.matmul(h,self.__oh)+self.__ob
            )
            h = tf.multiply(tf.nn.tanh(C),output_gate)
        return h

我们将这个类代替我们在第一部分所写的RNN的类即可。(白话：代码当中内容一定要仔细去看，如果有不清楚的地方，请在评论当中提出，我一定尽量解答。)

拓展

我们关于LSTM其实可以有各种各样的变化模式，比如说是双向的LSTM，多层的LSTM等。相关的代码都在代码链接有公开。大家可以自己下载去运行和分析。我在后续会发布LSTM的各种变种的方法的细致说明。

用keras调用库函数实现 RNN、LSTM(非计算机专业必须要掌握的方法)

当前，机器学习、神经网络已经成为非计算机专业研究人员的必备工具，keras背后是tensorflow2.0,tensorflow2.0变得更加适合于大家去调用，它摒弃了计算流图的思想，大家只需要调用库函数，就可以轻松搭建起自己的模型框架。让非计算机类的同学使用机器学习和神经网络的门槛变得更低了。我就给大家做一个使用多层LSTM处理本文所述任务的案例。

import pandas as pd
from keras.preprocessing.text import Tokenizer

%matplotlib inline
import re
from nltk.stem import WordNetLemmatizer
from nltk.corpus import stopwords
import keras
from sklearn.metrics import accuracy_score
data = pd.read_csv('train_17000.tsv',sep='\t')
test = pd.read_csv('test_7500.tsv',sep='\t')
def clear_review(text):
    texts = []
    for item in text:
        item = item.replace("

", "")
        item = re.sub("[^a-zA-Z]", " ", item.lower())
        texts.append(" ".join(item.split()))
    return texts
#删除停用词+词形还原
def stemed_words(text):
    stop_words = stopwords.words("english")
    lemma = WordNetLemmatizer()
    texts = []
    for item in text:
        words = [lemma.lemmatize(w, pos='v') for w in item.split() if w not in stop_words]
        texts.append(" ".join(words))
    return texts
#文本预处理
def preprocess(text):
    text = clear_review(text)
    text = stemed_words(text)
    return text
data_processed = preprocess(data.loc[:,'data'])
test_labels=test.loc[:,'labels']
test_processed = preprocess(test.loc[:,'data'])
print(type(data_processed))
data_processed = preprocess(data.loc[:,'data'])
test_labels=test.loc[:,'labels']
test_processed = preprocess(test.loc[:,'data'])
t = Tokenizer(num_words=6000)
t.fit_on_texts(data_processed+test_processed)
new_data = t.texts_to_sequences(data_processed)#用序号表示单词
new_sequence = keras.preprocessing.sequence.pad_sequences(new_data,maxlen=200
                ,padding='post',truncating='post')#将文本转换成统一长度n*200
'''
如下部分是keras搭建模型系统的方法，这么短的一段代码就能完成复杂的功能。
'''
model_lstm = keras.models.Sequential([
    keras.layers.Embedding(6000,32),#进行词向量的扩充，将数字扩展为32维
    keras.layers.LSTM(units=16,return_sequences=False),#LSTM处理模块
    keras.layers.LSTM(units=16,return_sequences=False),#第二个LSTM处理模块
    keras.layers.Dense(16,activation='relu'),#全连接层
    keras.layers.Dense(1,activation='sigmoid')#输出层
])
model_lstm.compile(optimizer='adam',loss='binary_crossentropy',metrics=['accuracy'])#配置模型的优化方法
history = model_lstm.fit(new_sequence,data.loc[:,'labels'],epochs=120)#开始训练，共训练120次。

#测试集数据预测
new_test = t.texts_to_sequences(test_processed)#用序号表示单词
new_sequence_test = keras.preprocessing.sequence.pad_sequences(new_test,maxlen=200
                ,padding='post',truncating='post')#将文本转换成统一长度n*200
results = model_lstm.predict_classes(new_sequence_test)#进行预测
print(accuracy_score(test_labels,results))#打印预测的准确率

• Python3.8
• Tensorflow2.2.0

当你要使用keras的时候，python的版本用最新的3.8即可，按照默认的方式安装tensorflow即可安装对应的tensorflow2.2.0版本。keras真的很方便，把你需要使用的模块添加到模型当中即可，keras把这些模块都已经封装好了。如果你不需要去修改模型内部的运算机制的话，我推荐使用keras，专注于自己领域内的东西即可。如果需要对这些诸如RNN、LSTM模块进行修改，我推荐使用tensorflow1.x来做研究，或者用pytorch来做研究。

博文推荐

我所编写的LSTM、RNN都是在强大的tensorflow所提供的反向传播下完成的，我只需要关心正向计算的流程即可。下面这个链接是将正向和反向过程都自己实现了一遍，非常厉害。
纯手工制作LSTM代码