【VRP】遗传算法之带时间窗的车辆路径问题【Matlab 041期】

一、VRP问题
车辆路径规划问题(Vehicle Routing Problem，VRP)一般指的是：对一系列发货点和收货点，组织调用一定的车辆，安排适当的行车路线，使车辆有序地通过它们，在满足指定的约束条件下（例如：货物的需求量与发货量，交发货时间，车辆容量限制，行驶里程限制，行驶时间限制等），力争实现一定的目标（如车辆空驶总里程最短，运输总费用最低，车辆按一定时间到达，使用的车辆数最小等）。

二、VRPTW问题
带时间窗的车辆路径规划问题(Vehicle Routing Problem with Time Window，VRPTW)是在VRP基础上添加配送时间约束条件产生的一个新问题。在这类问题中，给定车辆到达目的地的最早时间和最晚时间，要求车辆必须在规定的时间窗内到达，早于最早时间或晚于最晚时间都要产生额外的惩罚费用。此时，决策如何规划调度车辆使得配送的总费用最小化。

VRP与VRPTW对比：

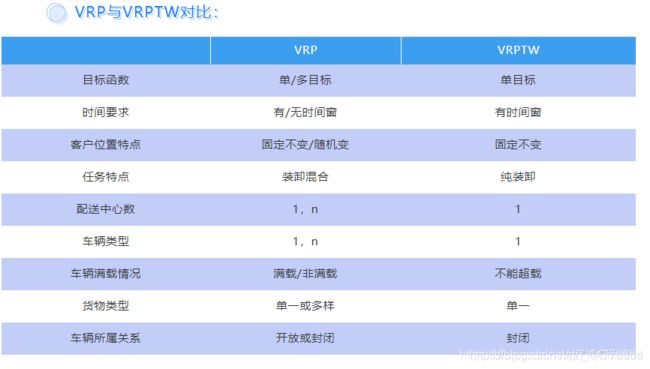
三、问题描述
本文将要研究的问题参考自文章《Fruit and Vegetable Agricultural Products Logistics Transport Routing Optimization - A Case Study of Qingdao blueberries distribution》。

某果蔬农产品运输配送中心 C0 (Center)。该配送中心有足够的能力满足顾客所有对果蔬农产品数量的要求。同时该配送中心有足够多且完全相同的车辆 J 能够完成配送活动的需要，运输车辆的最大容量为 V(Volume)，配送车辆在配送活动过程中均能一次到达，中间不会出现任何阻碍和特殊情况。C={C0 ,C1 ,C2 ……Cn }。其中 C0 代表配送中心。Ci (i=1,2, ……，n)(Consumer)表示有需求的客户的需求数量；n 表示有需求的客户数量。Dik (Distance)：表示顾客 Ci 到顾客 Ck 的距离（其中i不等于k）；Qdi (Quantity Demanded)：表示顾客 Ci 的需求量；Qg (Quality good):表示果蔬农产品刚刚采摘完，完好时的果蔬农产品的质量；[ETi ，LTi ]表示客户 Ci 对某类产品的时间窗约束。

在已知以上的条件情况下，合理安排最优的配送路线使得配送过程中满足所有条件情况下，各个费用之和最少。

四、数学模型
（具体模型参见（三）中文献）




五、算法设计
个体编码
遗传算法求解VRPTW的文献中有多种编码方式，这里对于个体采用自然数编码，代表配送中心，代表顾客；不同车辆的配送路线之间用0分隔（即每辆车都从仓库出发）；对于有个顾客，辆车的VRP问题来说，染色体长度为。

例如配送中心有3辆车为8个客户服务，一条可能的染色体如下：
0, 7, 0, 1, 2, 3, 5, 0, 8, 4, 6, 0
这条染色体表示的三辆车的行驶路线为:
第一辆车：0-7-0
第二辆车：0-1-2-3-5-0
第三辆车：0-8-4-6-0

惩罚
在交叉和突变产生的子代中，可能会有两种违反约束的形式：

车辆超载
不能在时间窗口约束给出的最晚时间点内到达指定顾客处
对这两种违反约束的情况采用静态惩罚，考虑到时间窗口更容易被违反，对其施加较大的惩罚因子。对这两种约束违反的惩罚因子分别设置为10和500。

交叉
这里参考《基于电动汽车的带时间窗的路径优化问题研究》中给出的交叉操作

突变
对选中的个体中各条子路线用2-opt算法优化

选择
育种选择：binary锦标赛选择
环境选择：采用精英保留策略，合并子代和父代后，选择数量等同于族群规模的个体
%

%
clear
clc
close all
tic
%% 用importdata这个函数来读取文件
c101=importdata(‘c101.txt’);
vehicle_info = [2 4 350 50;
3 6 350 50;
6 15 450 100;
10 17 550 110;
13 30 650 140;
15 40 650 140;
25 50 850 180];
cap=200; %车辆最大装载量
%% 提取数据信息
E=c101(1,5); %配送中心时间窗开始时间
L=c101(1,6); %配送中心时间窗结束时间
vertexs=c101(:,2:3); %所有点的坐标x和y
customer=vertexs(2:end,:); %顾客坐标
cusnum=size(customer,1); %顾客数
v_num=21; %车辆最多使用数目
demands=c101(2:end,4); %需求量
a=c101(2:end,5); %顾客时间窗开始时间[a[i],b[i]]
b=c101(2:end,6); %顾客时间窗结束时间[a[i],b[i]]
s=c101(2:end,7); %客户点的服务时间
h=pdist(vertexs);
dist=squareform(h); %距离矩阵，满足三角关系，暂用距离表示花费c[i][j]=dist[i][j]
%% 遗传算法参数设置
alpha=10; %违反的容量约束的惩罚函数系数
belta=100; %违反时间窗约束的惩罚函数系数
NIND=100; %种群大小
MAXGEN=100; %迭代次数
Pc=0.9; %交叉概率
Pm=0.05; %变异概率
GGAP=0.9; %代沟(Generation gap)
N=cusnum+v_num-1; %染色体长度=顾客数目+车辆最多使用数目-1
%% 初始化种群
init_vc=init(cusnum,a,demands,cap); %构造初始解
Chrom=InitPopCW(NIND,N,cusnum,init_vc);
%% 输出随机解的路线和总距离
disp(‘初始种群中的一个随机值:’)
[VC,NV,TD,violate_num,violate_cus]=decode(Chrom(1,:),cusnum,cap,demands,a,b,L,s,dist);
% disp([‘总距离：’,num2str(TD)]);
disp([‘车辆使用数目：’,num2str(NV),’，车辆行驶总距离：’,num2str(TD),’，违反约束路径数目：’,num2str(violate_num),’，违反约束顾客数目：’,num2str(violate_cus)]);
disp(’~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~’)
%% 优化
gen=1;
figure;
hold on;box on
xlim([0,MAXGEN])
title(‘优化过程’)
xlabel(‘代数’)
ylabel(‘最优值’)
ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta); %计算种群目标函数值
preObjV=min(ObjV);
while gen<=MAXGEN
%% 计算适应度
ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta); %计算种群目标函数值
line([gen-1,gen],[preObjV,min(ObjV)]);pause(0.0001)
preObjV=min(ObjV);
FitnV=Fitness(ObjV);
%% 选择
SelCh=Select(Chrom,FitnV,GGAP);
%% OX交叉操作
SelCh=Recombin(SelCh,Pc);
%% 变异
SelCh=Mutate(SelCh,Pm);
%% 局部搜索操作
SelCh=LocalSearch(SelCh,cusnum,cap,demands,a,b,L,s,dist,alpha,belta);
%% 重插入子代的新种群
Chrom=Reins(Chrom,SelCh,ObjV);
%% 删除种群中重复个体，并补齐删除的个体
Chrom=deal_Repeat(Chrom);
%% 打印当前最优解
ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta); %计算种群目标函数值
[minObjV,minInd]=min(ObjV);
disp([‘第’,num2str(gen),‘代最优解:’])
[bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(Chrom(minInd(1),cusnum,cap,demands,a,b,L,s,dist);
disp([‘车辆使用数目：’,num2str(bestNV),’，车辆行驶总距离：’,num2str(bestTD),’，违反约束路径数目：’,num2str(best_vionum),’，违反约束顾客数目：’,num2str(best_viocus)]);
fprintf(’\n’)
%% 更新迭代次数
gen=gen+1 ;
end
%% 画出最优解的路线图
ObjV=calObj(Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta); %计算种群目标函数值
[minObjV,minInd]=min(ObjV);
%% 输出最优解的路线和总距离
disp(‘最优解:’)
bestChrom=Chrom(minInd(1);
[bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(bestChrom,cusnum,cap,demands,a,b,L,s,dist);
disp([‘车辆使用数目：’,num2str(bestNV),’，车辆行驶总距离：’,num2str(bestTD),’，违反约束路径数目：’,num2str(best_vionum),’，违反约束顾客数目：’,num2str(best_viocus)]);
disp(’-------------------------------------------------------------’)
%% 判断最优解是否满足时间窗约束和载重量约束，0表示违反约束，1表示满足全部约束
flag=Judge(bestVC,cap,demands,a,b,L,s,dist);
%% 检查最优解中是否存在元素丢失的情况，丢失元素，如果没有则为空
DEL=Judge_Del(bestVC);
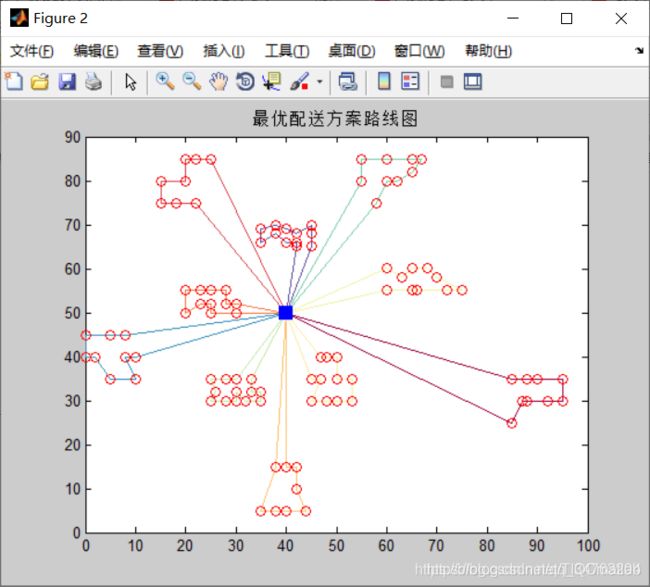
%% 画出最终路线图
draw_Best(bestVC,vertexs);
save c101.mat
toc

四、备注

完整代码或者代写添加QQ912100926。
往期回顾>>>>>>
【路径规划】粒子群优化算法之三维无人机路径规划【Matlab 012期】
【路径规划】遗传算法之多物流中心的开放式车辆路径规划【Matlab 013期】
【路径规划】粒子群算法之机器人栅格路径规划【Matlab 014期】
【路径规划】蚁群算法之求解最短路径【Matlab 015期】
【路径规划】免疫算法之物流中心选址【Matlab 016期】
【路径规划】人工蜂群之无人机三维路径规划【Matlab 017期】
【路径规划】遗传算法之基于栅格地图机器人路径规划【Matlab 018期】
【路径规划】蚁群算法之多无人机攻击调度【Matlab 019期】
【路径规划】遗传算法之基于栅格地图的机器人最优路径规划【Matlab 020期】
【路径规划】遗传算法之考虑分配次序的多无人机协同目标分配建模【Matlab 021期】
【路径规划】蚁群算法之多中心vrp问题【Matlab 022期】
【路径规划】蚁群算法之求解带时间窗的多中心VRP【Matlab 023期】
【路径规划】遗传算法之多中心VRP求解【Matlab 024期】
【路径规划】模拟退火之求解VRP问题【Matlab 025期】
【路径规划】A星之栅格路径规划【Matlab 026期】
【路径规划】基于一种带交叉因子的双向寻优粒子群栅格地图路径规划【Matlab 027期】
【路径规划】【TSP】蚁群算法之求解TSP问题含GUI【Matlab 028期】
【路径规划】蚁群算法之栅格地图路径规划【Matlab 029期】
【路径规划】遗传算法之旅行商 TSP 【Matlab 030期】
【路径规划】模拟退火算法之旅行商 TSP 问题【Matlab 031期】
【路径规划】蚁群算法之智能车路径规划【Matlab 032期】
【路径规划】华为杯：基于matlab 无人机优化运用于抢险救灾【Matlab 033期】
【路径规划】matlab之最小费用最大流算问题【Matlab 034期】
【路径规划】A*算法之解决三维路径规划问题【Matlab 035期】
【路径规划】人工蜂群算法之路径规划【Matlab036期】
【路径规划】人工蜂群算法之路径规划【Matlab 037期】
【路径规划】蚁群算法之求解多旅行商MTSP问题【Matlab 038期】
【路径规划】蚁群算法之无人机路径规划【Matlab 039期】

【路径规划】遗传算法之求解多VRP问题【Matlab 040期】