蚂蚁算法matlab
蚂蚁算法解决旅行商问题
1.简介
蚁群算法是一种用来寻找优化路径的概率型算法。它由Marco Dorigo于1992年在他的博士论文中提出,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。 [1]
这种算法具有分布计算、信息正反馈和启发式搜索的特征,本质上是进化算法中的一种启发式全局优化算法。
2.算法原理
TSP求解中,假设蚁群算法中的每只蚂蚁是具有以下特征的简单智能体:每次周游,每只蚂蚁在其经过的支路(i.j)上都留下信息素。蚂蚁选择城市的概率与城市之间的距离和当前连接之路上所包含的信息素余量有关。禁忌表用来控制蚂蚁以走访过的城市。
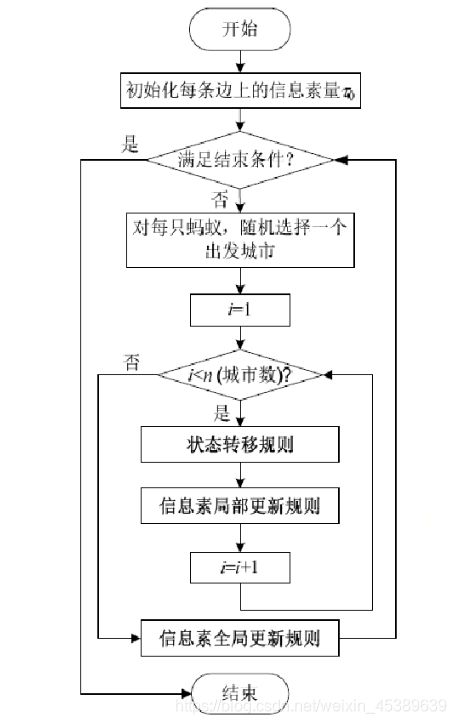
2.1算法参数函数分析
函数分析:
路劲构建:作为蚂蚁访问下一个城市选择的依据
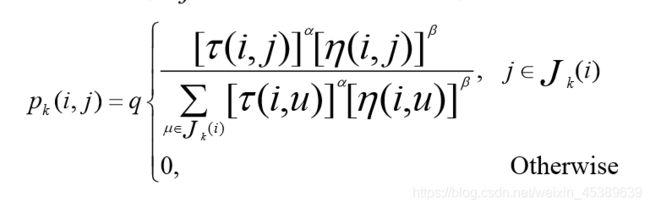
信息素更新:ρ是信息素的挥发率,Δτij是第k只蚂蚁在它经过的 边上释放的信息素量,它等于蚂蚁k本轮构建路径长度的 倒数。Ck表示路径长度,它是Rk中所有边的长度和。
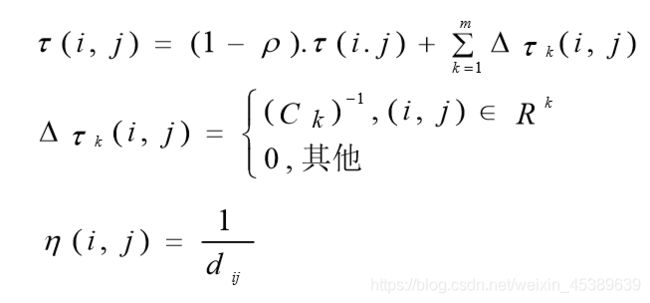
参数分析:
蚂蚁数量:蚂蚁的数量决定了信息素变化,同时数量的过多过少可能会导致找不到全局最优解。所以蚂蚁的数量一般设定为城市数量的1.5倍。
信息素因子:信息素因子是蚂蚁在搜索中重要的向导,其值过大,蚂蚁选择以前走过的路劲概率会大大提高,搜索随机性会减少,其值过小则容易使陷入局部最优。
启发函数因子:反映的是蚁群寻优过程中先验性和确定性因素的作用强度。过大时,虽然收敛速度会加快,但容易陷入局部最优,过小时容易陷入随机搜索,找不到最优解。
信息挥发率:表示信息素的消失水平,它的大小直接关系刀蚁群算法的全局搜索能力和收敛速度。
最大迭代次数:最大迭代次数过小,可能导致算法还没收敛就结束了,过大则会导致浪费资源,本文中实验次数取100次。
3.matlab具体实现
3.1代码截图
%% 旅行商问题(TSP)优化
%% 清空环境变量
clear all
clc
%% 导入数据
load citys_data.mat
%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n');
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
for j = 1:n
if i ~= j
D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
else
D(i,j) = 1e-4;
end
end
end
%% 初始化参数
fprintf('Initializing Parameters... \n');
m = 50; % 蚂蚁数量
alpha = 3; % 信息素重要程度因子
beta = 3; % 启发函数重要程度因子
rho = 0.3; % 信息素挥发因子
Q = 1; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 100; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度
%% 迭代寻找最佳路径
figure;
while iter <= iter_max
fprintf('迭代第%d次\n',iter);
% 随机产生各个蚂蚁的起点城市
start = zeros(m,1);
for i = 1:m
temp = randperm(n);
start(i) = temp(1);
end
Table(:,1) = start;
% 构建解空间
citys_index = 1:n;
% 逐个蚂蚁路径选择
for i = 1:m
% 逐个城市路径选择
for j = 2:n
tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)
allow_index = ~ismember(citys_index,tabu);
allow = citys_index(allow_index); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = 1:length(allow)
P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
end
P = P/sum(P);
% 轮盘赌法选择下一个访问城市
Pc = cumsum(P);
target_index = find(Pc >= rand);
target = allow(target_index(1));
Table(i,j) = target;
end
end
% 计算各个蚂蚁的路径距离
Length = zeros(m,1);
for i = 1:m
Route = Table(i,:);
for j = 1:(n - 1)
Length(i) = Length(i) + D(Route(j),Route(j + 1));
end
Length(i) = Length(i) + D(Route(n),Route(1));
end
% 计算最短路径距离及平均距离
if iter == 1
[min_Length,min_index] = min(Length);
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length);
Route_best(iter,:) = Table(min_index,:);
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - 1),min_Length);
Length_ave(iter) = mean(Length);
if Length_best(iter) == min_Length
Route_best(iter,:) = Table(min_index,:);
else
Route_best(iter,:) = Route_best((iter-1),:);
end
end
% 更新信息素
Delta_Tau = zeros(n,n);
% 逐个蚂蚁计算
for i = 1:m
% 逐个城市计算
for j = 1:(n - 1)
Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
end
Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
% 迭代次数加1,清空路径记录表
% figure;
%最佳路径的迭代变化过程
[Shortest_Length,index] = min(Length_best(1:iter));
Shortest_Route = Route_best(index,:);
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
pause(0.3);
iter = iter + 1;
Table = zeros(m,n);
% end
end
%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
%% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
text(citys(i,1),citys(i,2),[' ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
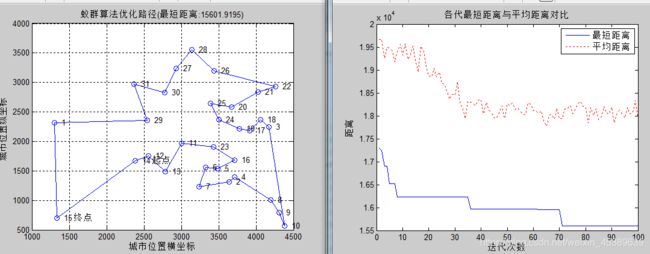
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')
3.2结果截图及分析
为了更好的确定信息素因子启发函数因子及挥发因子之间的关系,采取控制变量的方式得取实验结果进行一一比较,得出最优解数据确定三个因子的取值。
确定不变的变量:
蚂蚁数量=50,迭代次数=100次
1 alpha=1,beta=3,rho=0.3
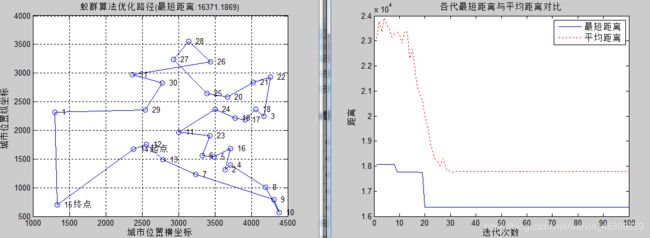
2 alpha=2,beta=3,rho=0.3
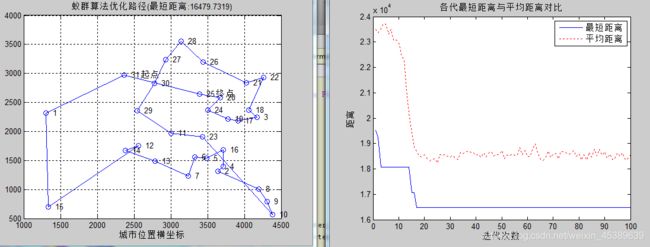
3 alpha=3,beta=3,rho=0.3
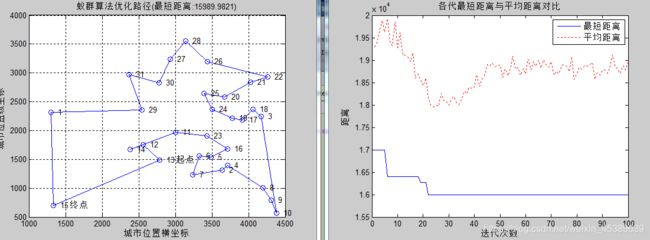
小结:改变alpha(信息素重要程度),通过观察发现增高alpha值提高了函数的收敛速度,但陷入了局部最优不能找到函数的最优解,其原因是alpha增高了,降低了蚁群的随机搜索性,最后通过对比,发现当alpha=2使函数有了比较明显的优化,故将alpha改为2。
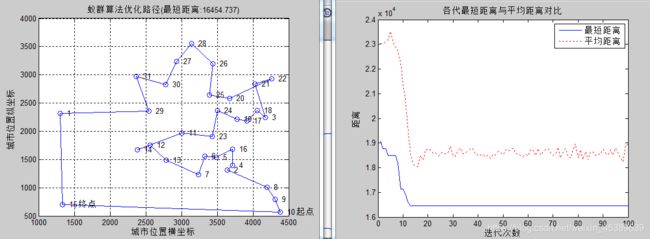
4 alpha=2,beta=4,rho=0.3
小结:本图修改了beta(函数启发因子)为4。所求得得最短路径随之变化,它表现的是启发式信息在指导蚁群搜索过程之中相对重要的程度,它的大小影响着蚁群在整个寻短过程中的先验性和确定性。将4图和图2进行比较,发现收敛速度无明显增加,且陷入了局部最优。故beta不修改。
5 alpha=2,beta=3,rho=0.4
小结:本阶段将修改rho(信息素挥发度)来找到最优rho,本图5与图2进行比较,收敛速度明显加快,但依旧陷入局部最优。故不做修改,继续修改rho值实验。
6 alpha=2,beta=3,rho=0.5
小结:本图6与图2相比依旧为局部最优故增加rho只能降低蚁群的搜索不确定性,故增大rho不做讨论。
7 alpha=2,beta=3,rho=0.2
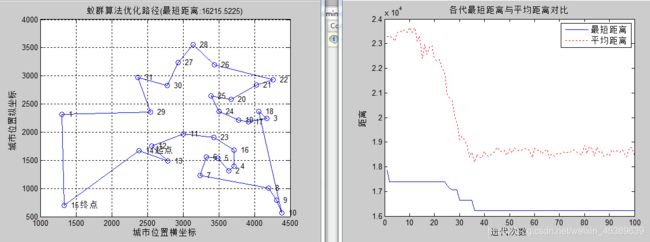
小结:本图7与图2比较收敛速度明显下降,且任然为局部最优。故rho最优值确立为3。
3.3总结:
本实验通过比较得出alpha=2,beta=3,rho=3为最优,除此之外得出了rho的大小直接影响了蚁群算法的全局搜索能力和收敛速度。各个参数实际上都直接或间接得影响着蚁群的搜索能力及收敛速度。同时蚁群算法的优点也显而易见。在解决最短路径长度这一块,蚁群能很快得得出几十几百甚至成千上万个城市之间得旅行商问题。在实际生活中生产中,蚁群算法还可以解决其他一些问题,通过改良版的蚁群优化算法有更高效的执行效率,例如光网络的智能化管理,计算机网络路由,聚类问题等等。