sklearn主成分分析PCA

sklearn主成分分析PCA

菜菜的sklearn学习笔记

数学原理

给数学基础不是很好的看
PCA主要用于降维，比如一个人有身高，年龄，样貌，性别，智力，耐力，速度，成绩等等很多特征，每种特征便是一个维度。假如你觉得描述一个人的特征太多，你想要用一两个或几个特征就个以描述一个人，并且这几个特征包含之前提到所有特征所包含的信息，将这么原来的众多特征转化为几个特征的过程就是降维。而降维后得到的特征包含的信息量的多少也叫做贡献率，信息量越多越能够反应本质。

代码

这里举一个最常用的水仙花的例子

导入包

包括sklearn他的好基友们啦。

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import pandas as pd
import numpy as np

导入数据

这是一个水仙花的案例

iris = load_iris()
y = iris.target
x = iris.data

有x.shape = (150, 4),即每朵花共有四个特征,分别为

iris.feature_names = 
                    ['sepal length (cm)',
                     'sepal width (cm)',
                     'petal length (cm)',
                     'petal width (cm)']

而y是一个分类变量，分别为[0,1,2]代表三种不同的花

核心代码

还是sklearn中的老三样:

• 实例化PCA()
• 调用fit()函数
• 调用transform()函数

pca = PCA(n_components = 2)
pca = pca.fit(x)
x_dr = pca.transform(x)

这里n_components表示降维后所得到的维度
或者也可以直接一步到位

x_dr = PCA(2).fit_transform(x)

查看降维后所带有的信息量大小

• 两个维度信息量大小

print(pca.explained_variance_)

可以得到[4.22824171， 0.24267075]

• 两个维度贡献率

pca.explained_variance_ratio_

可以得到[0.92461872, 0.05306648]

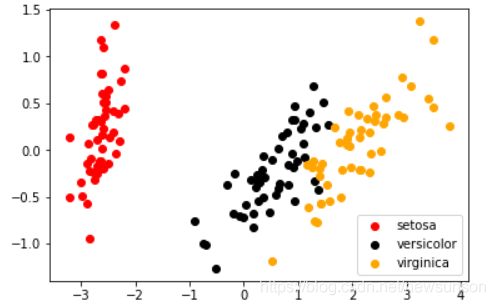
可视化

当我们把数据降维后，可以观察其在新的维度上的分布

plt.figure()
plt.scatter(x_dr[y == 0,0],x_dr[y == 0,1],c = "red",label = iris.target_names[0])
plt.scatter(x_dr[y == 1,0],x_dr[y == 1,1],c = "black",label = iris.target_names[1])
plt.scatter(x_dr[y == 2,0],x_dr[y == 2,1],c = "orange",label = iris.target_names[2])
plt.legend()
plt.show()

其中x_dr[y = 0,0]用了布尔索引

得到如下结果

可以这是一个分簇的分布，也就是说降维之后其实已经比较好分类了

扩展

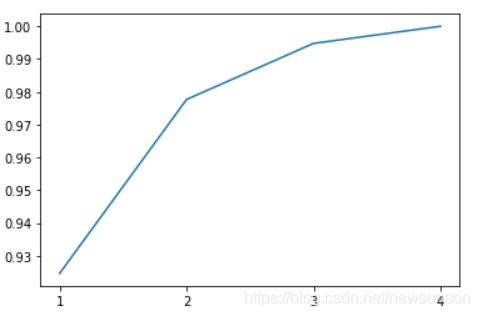
累计方差贡献率曲线

当选取维度不同时累计贡献率的曲线。

pca_line = PCA().fit(x)
plt.plot([1,2,3,4],np.cumsum(pca_line.explained_variance_ratio_))
plt.xticks([1,2,3,4])
plt.show()

最大似然估计选择超参数

这种方法可以自动选出最合适的维度

pca_mle = PCA(n_components = "mle")
pca_mle = pca_mle.fit(x)
x_mle = pca_mle.transform(x)
pca_mle.explained_variance_ratio_.sum()

比如上述例子为我们选了维度为3，累计贡献率高达0.994

按贡献率选择

意味着你想要他的累计贡献率达到0.97时的维度。

pca_f = PCA(n_components=0.97,svd_solver="full")
pca_f = pca_f.fit(x)
x_f = pca_f.transform(x)
print(pca_f.explained_variance_ratio_)

贡献率分别为[0.92461872, 0.05306648]