【数字图像处理2.1 】频率域中的 高通滤波 和 低通滤波 Python+Opencv+Numpy

前言

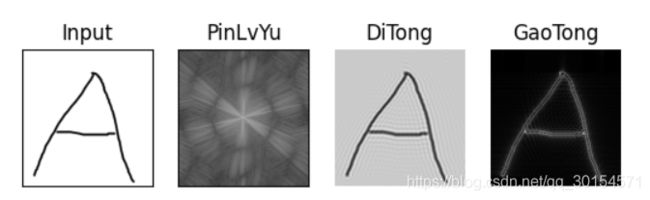
1、图像的高频信息往往是细节+噪声；中频信息一般是图像的框架信息；低频信息数量最多，是图形的主体

2、所以，高通滤波器，只通过高频信息，所以留下来的图像只有边缘等细节信息，看起来像简笔画。低通滤波器同理。

3、本次练习的【高通滤波】和 【低通滤波】，都是【频率域】中的概念，而之前做的练习：【直方图】啊、【平滑滤波器】都是作用在【空间域】的算法。

4、我在最后，会对频率域算法和空间域算法进行对比总结。

1、实验目的

• 通过对图像进行高通滤波、低通滤波等操作，观察结果，对比频率域算法和空间域算法的异同。

另一个实验——同态滤波器的效果、总结在此：

https://blog.csdn.net/qq_30154571/article/details/109138478

2、频率域中高通、低通的效果图

补充：第一次作业（空间域各种滤波器实验）的效果：

https://blog.csdn.net/qq_30154571/article/details/109065550

3、代码

import numpy as np
import matplotlib.pyplot as plt
import cv2
###################################################################
###############            进行频率域处理             #############
###################################################################

img = cv2.imread("pic/6.png",0)#读图
dft = cv2.dft(np.float64(img),flags = cv2.DFT_COMPLEX_OUTPUT)#设置输入格式为float32
dft_shift = np.fft.fftshift(dft)#低频分量中心化处理，方便观察

#设置振幅大小
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

#打印输入图像
plt.subplot(141), plt.imshow(img, cmap='gray')
plt.title('Input'), plt.xticks([]), plt.yticks([])

#获取频谱图
plt.subplot(142), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('PinLvYu'), plt.xticks([]), plt.yticks([])

###################################################################
###############            进行低通滤波             #############
###################################################################

#设置低通滤波器
rows, cols = img.shape
crow,ccol = int(rows/2), int(cols/2) #中心位置
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1#设置矩形窗口遮罩，设为1，过滤高频

#掩膜图像和频谱图像乘积
f = dft_shift * mask

#傅里叶逆变换
ishift = np.fft.ifftshift(f)
iimg = cv2.idft(ishift)
res = cv2.magnitude(iimg[:,:,0], iimg[:,:,1])

#显示低通滤波处理图像
plt.subplot(143), plt.imshow(res, 'gray'), plt.title('DiTong')
plt.axis('off')

########################################################################
###################          进行高通滤波         ######################
########################################################################

f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)

#设置高通滤波器
rows, cols = img.shape
crow,ccol = int(rows/2), int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0#设置矩形窗口遮罩，设为0，过滤低频

#傅里叶逆变换
ishift = np.fft.ifftshift(fshift)
himg = np.fft.ifft2(ishift)
himg = np.abs(himg)

#显示高通滤波处理图像
plt.subplot(144), plt.imshow(himg, 'gray'), plt.title('GaoTong')
plt.axis('off')
plt.show()

参考：https://www.jianshu.com/p/01ae3df005d0

4、空间域滤波 与 频率域滤波比较

(1)、回顾空间滤波

在比较二者之前，先做一下简单的知识回顾和梳理：

• 之前用到的图像域的滤波器，大部分都是线性滤波（除了中值滤波，因为中值这个概念是一个统计学的概念，并不是一个能直接加减乘除的概念）。
• 线性滤波的包含方框滤波、均值滤波、高斯滤波、拉普拉斯滤波、梯度算子等。
• 而线性滤波在具体操作上，会涉及到一个模板的概念，简单来说就是一个3X3（一般是3X3）的矩阵，最中间的点就是我们的输入点，而周围的八个点，就是我们要改变的周围像素块的值。（有点类似于卷积核和原图像的关系）
• 均值滤波模板：
• 拉普拉斯模板
  

(2)、相同点：

将第一次作业习中所用到的模板（就是那个各种3X3的矩阵），处理图像后，再进行频率域化+中心化处理，效果如下图：

有图可得知：第一次作业用到的空间域的【拉布拉斯算子处理】和【梯度算子处理】，在功能上近似于高通滤波器，二者和本次练习中的频率域高通、低通都能达到基本相同的功能；均值滤波、中值滤波在功能上也基本属于低通滤波器。

(3)、不同点：

• 图像的空间域处理，主要是对像素灰度值的改变，其元素本身位置不变。

• 频率域是以频谱表示信息分布特征，原图像上的灰度突变部位、图像结构复杂的区域、图像细节及干扰噪声等信息集中在高频区，而原图像上灰度变化平缓部位的信息集中在低频区。

• 在频率域，一些特性比较突出，容易处理。比如在空间图像里不好找出噪声的模式，如果变换到频率域，则比较好找出噪声的模式，并能更容易的处理。

• 补充：傅立叶变换能把遥感图像从空间域变换到只包含不同频率信息的频率域。也就是说，傅里叶变换是连接二者的桥梁。

(4)、二者关系：

空间域与空间频率域可互相转换。在空间频率域中可以引用已经很成熟的频率域技术,处理的一般步骤为：

• 对图像施行二维离散傅立叶变换或小波变换,将图像由图像空间转换到频域空间。
• 在空间频率域中对图像的频谱作分析处理,以改变图像的频率特征。即设计不同的数字滤波器,对图像的频谱进行滤波。频率域处理主要用于与图像空间频率有关的处理中。

总结，空间域的图像处理，在数学上，在逻辑上，相比于频率域更加简单直观，而频域更适合做分析，因为有一些细节在图像域展现的不明显。二者各有各的用途，分析和工程，都是重要的应用。