基于C++的带权无向图的实现 (二)- 遍历算法
该系列文章是本人整理的有关带权无向图的数据结构和算法的分析与实现,如有问题或者建议欢迎各位指出。
目录
基于C++的带权无向图的实现 (一)- 数据结构
基于C++的带权无向图的实现 (二)- 遍历算法
基于C++的带权无向图的实现 (三)- Prim最小生成树算法
基于C++的带权无向图的实现 (四)- Dijkstra最短路径算法
图的遍历算法
图的遍历,其实就是依次访问图中所有的结点,并且不能访问重复结点,也就是说已经访问过的结点需要做上标记。
图的遍历分为两种两种算法:
- 深度优先遍历算法(DFT)或者深度优先搜索算法(DFS)
- 广度优先遍历算法(BFT)或者广度优先搜索算法(BFS)
本文将介绍这两种算法的思想和代码实现思路。
深度优先遍历
深度优先遍历,简单来说就是一条路走到底,然后退一步再把另一条路走到底,依此类推访问完图中的所有结点。二叉树的前中后序遍历其实就是深度优先遍历。
该算法可以通过递归和迭代的方法实现递归来实现。
递归
- 访问起始顶点u,标记顶点u为“已访问”的状态。
- 对顶点u的第一个未访问的结点v进行深度访问,每次访问的时候都会将邻接点标记为“已访问”的状态,避免重复访问。
- 当遇到死胡同时回溯到之前记录的未访问过的邻接点,再进行深度访问,直到遍历完整个图。
拿上一节中出现的图来举例子,对于下图,如果从顶点A开始深度优先遍历(红色用来标记已经访问过的顶点,蓝色用来表示访问路径):

首先,对A的邻居进行遍历,顶点A的邻居依次为B,D,接着递归访问顶点B。

再对顶点B的邻居进行遍历,顶点B的邻居依次为A,C,D,E,由于A已经访问过了,所以访问顶点C。

再对顶点C的邻居进行遍历,顶点C的邻居依次为B,E,由于B已经访问过了,所以访问顶点E。

再对顶点E的邻居进行遍历,顶点C的邻居依次为B,C,D,F,G,由于B,C已经访问过了,所以访问顶点D。

再对顶点D的邻居进行遍历,顶点D的邻居依次为A,B,E,F,由于A,B,E都已经访问过了,所以访问顶点F。
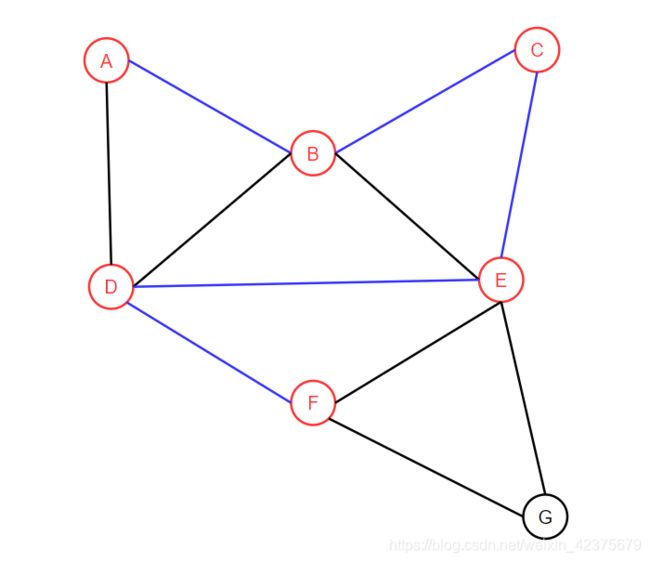
再对顶点F的邻居进行遍历,顶点D的邻居依次为D,E,G,由于D,E都已经访问过了,所以访问顶点G。
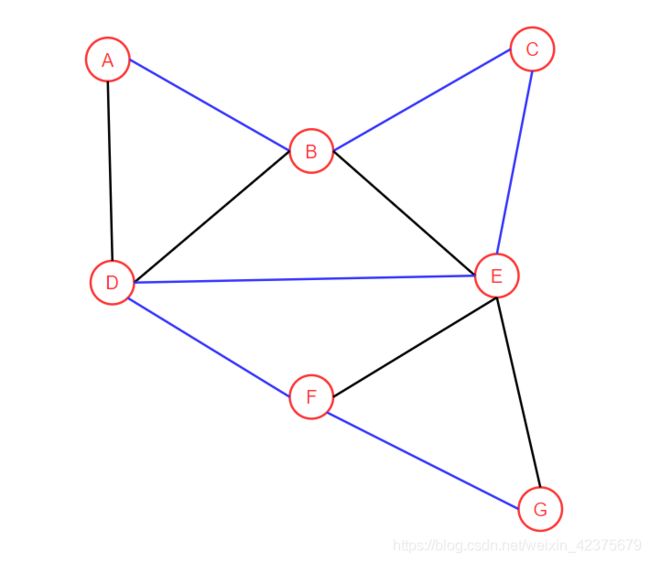
所有结点访问完毕,遍历结束。
递归法深度优先遍历的结果为: A B C E D F G
迭代(需要用到栈)
迭代法本质上和递归实现的步骤一样,但由于栈是先入后出的数据结构,所以实际上每次都是对顶点u的最后一个顶点v进行深度遍历,例子如下:
从顶点A开始深度优先遍历,在访问顶点A前,先将顶点A压入栈,如下所示:

弹出栈顶元素A,表示开始访问顶点A,然后遍历顶点A的所有邻居,将未访问过的邻居压入栈,这里A的邻居为B,D。由于所有邻居均未访问过,所以将B,D压入栈。

弹出栈顶元素D,表示开始访问顶点D,然后遍历顶点D的所有邻居,将未访问过的邻居压入栈,这里D的邻居为A,B,E,F。由于A已经访问过了,所以将B,E,F压入栈。

弹出栈顶元素F,表示开始访问顶点F,然后遍历顶点F的所有邻居,将未访问过的邻居压入栈,这里F的邻居为D,E,G。由于D已经访问过了,所以将E,G压入栈。

弹出栈顶元素G,表示开始访问顶点G,然后遍历顶点G的所有邻居,将未访问过的邻居压入栈,这里G的邻居为E,F。由于F已经访问过了,所以将E压入栈。

弹出栈顶元素E,表示开始访问顶点E,然后遍历顶点E的所有邻居,将未访问过的邻居压入栈,这里E的邻居为B,C,D,F,G。由于D,F,G已经访问过了,所以将B,C压入栈。

弹出栈顶元素C,表示开始访问顶点C,然后遍历顶点E的所有邻居,将未访问过的邻居压入栈,这里C的邻居为B,E。由于E已经访问过了,所以将B压入栈。

弹出栈顶元素B,表示开始访问顶点B,然后遍历顶点B的所有邻居,将未访问过的邻居压入栈,这里B的邻居为A,C,D,E。由于所有邻接顶点已经访问过了,此时不会压入元素入栈。

到这里其实已经遍历完了,但是栈内还剩五个元素,依次是BEEBB。由于B,E顶点已经访问过了,所以每次弹出栈顶元素都不会再访问图中的任何一个顶点了,直到五个元素全部弹出,栈为空时遍历才算完全结束。
迭代法深度优先遍历的结果为:A D F G E C B
广度优先遍历
广度优先遍历比深度优先遍历更好理解,简单来说就是逐层遍历,图的第一层(初始点)遍历完后开始遍历第二层,然后是第三层。实现广度优先遍历一般需要借用到先入先出的“队列”这种结构。
继续拿刚刚的图来举例,从顶点A开始广度优先遍历,在访问顶点A前,先将顶点A入队,如下所示:
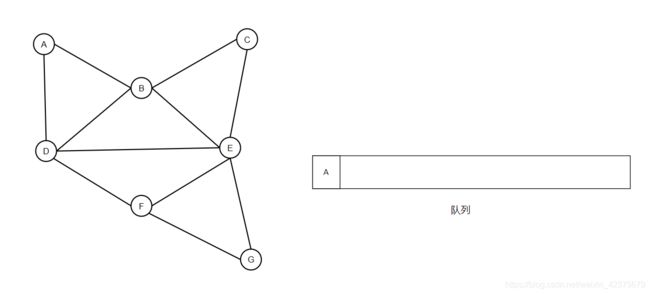
队列首元素A出队,表示开始访问顶点A,然后遍历顶点A的所有邻居,将未访问过的邻居压入队,这里A的邻居为B,D。由于所有邻居均未访问过,所以将B,D入队。

队列首元素B出队,表示开始访问顶点B,然后遍历顶点B的所有邻居,将未访问过的邻居压入队,这里A的邻居为C,E,D。由于所有邻居均未访问过,所以将C,E,D入队。

队列首元素D出队,表示开始访问顶点D,然后遍历顶点D的所有邻居,将未访问过的邻居压入队,这里D的邻居为A,B,E,F。由于A和B已经访问过了,所以将E,F入队。

队列首元素C出队,表示开始访问顶点C,然后遍历顶点C的所有邻居,将未访问过的邻居压入队,这里C的邻居为B,E。由于B已经访问过了,所以将E入队。

队列首元素E出队,表示开始访问顶点E,然后遍历顶点E的所有邻居,将未访问过的邻居压入队,这里E的邻居为B,C,D,F,G。由于B,C,D已经访问过了,所以将F,G入队。

队列首元素D出队,发现D已经访问过了,所以跳过。接着出队E,发现E也访问过了。然后出队F,发现F还没访问过,因此访问顶点F,然后遍历顶点F的所有邻居,将未访问过的邻居压入队,这里F的邻居为D,E,G。由于D,E已经访问过了,所以将G入队。

队列首元素E出队,发现E已经访问过了,所以跳过。接着出队F,发现F也访问过了。然后出队G,发现G还没访问过,因此访问顶点G,然后遍历顶点G的所有邻居,将未访问过的邻居压入队,这里F的邻居为E,F。由于E,F都已经访问过了,所以不会再有新元素入队。
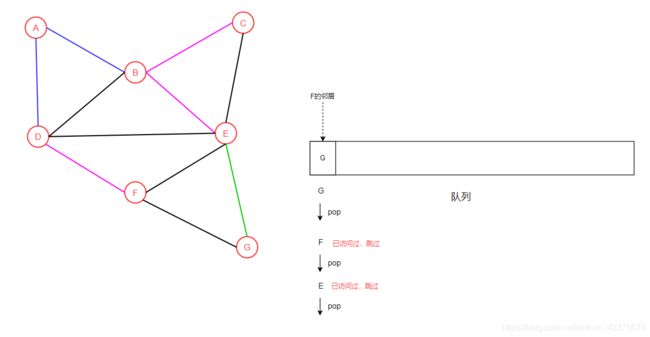
最后队列首元素G出队,发现G已经访问过了,队列为空,遍历完全结束。
广度优先遍历结果: A B D C E F G
代码实现
在Graph类中除了上节内容实现的功能外,额外添加了遍历算法,T为提前定义好的模板:
| 函数名 | 用途 |
|---|---|
| void dft_recursion(const T& u, set& visited, vector& result) | 深度优先遍历(递归辅助函数) |
| vector depth_first_rec(const T& u); | 深度优先遍历(递归) |
| vector depth_first_itr(const T& u); | 深度优先遍历(迭代) |
| vector breadth_first(const T& u); | 广度优先遍历(迭代) |
- 边的定义(edge.hpp):
template <typename T>
class Edge {
public:
T vertex;
int weight;
Edge(T neighbour_vertex) {
this->vertex = neighbour_vertex;
this->weight = 0;
}
Edge(T neighbour_vertex, int weight) {
this->vertex = neighbour_vertex;
this->weight = weight;
}
bool operator<(const Edge& obj) const {
return obj.vertex > vertex;
}
bool operator==(const Edge& obj) const {
return obj.vertex == vertex;
}
};
- 图的定义(graph.hpp)
#include由于图的函数声明除了最后四个其他的都在前一节中实现了,所以这里只放后面四个函数的实现代码(graph.hpp):
template <typename T> void Graph<T>::dft_recursion(const T& u, set<T>& visited, vector<T>& result) {
result.push_back(u);
visited.insert(u);
for (Edge<T> edge : adj[u])
if (visited.find(edge.vertex) == visited.end())
dft_recursion(edge.vertex, visited, result);
}
template <typename T> vector<T> Graph<T>::depth_first_rec(const T& u) {
vector<T> result;
set<T> visited;
if (contains(u)) dft_recursion(u, visited, result);
return result;
}
template <typename T> vector<T> Graph<T>::depth_first_itr(const T& u) {
vector<T> result;
set<T> visited;
stack<T> s;
s.push(u);
while (!s.empty()) {
T v = s.top();
s.pop();
if (visited.find(v) != visited.end()) {
continue;
}
visited.insert(v);
result.push_back(v);
for (auto w : adj[v]) {
if (visited.find(w.vertex) == visited.end()) {
s.push(w.vertex);
}
}
}
return result;
}
template <typename T> vector<T> Graph<T>::breadth_first(const T& u) {
vector<T>result;
set<T> visited;
queue<T> q;
q.push(u);a
while (!q.empty()) {
T v = q.front();
q.pop();
if (visited.find(v) != visited.end()) {
continue;
}
visited.insert(v);
result.push_back(v);
for (Edge<T> edge : adj[v]) {
if (visited.find(edge.vertex) == visited.end()) {
q.push(edge.vertex);
}
}
}
return result;
}
测试
测试案例(graph_testing.cpp):
#include "graph.hpp"
void test02(Graph<char> g)
{
auto dft = g.depth_first_rec('A');
cout << "从顶点A进行深度优先遍历(递归): {";
for (auto u : dft) cout << u << " ";
cout << "}" << endl;
vector<char> dft_itr = g.depth_first_itr('A');
cout << "从顶点A进行深度优先遍历(迭代): {";
for (auto u : dft_itr) cout << u << " ";
cout << "}" << endl;
auto bft = g.breadth_first('A');
cout << "从顶点A进行广度优先遍历: {";
for (auto u : bft) cout << u << " ";
cout << "}" << endl;
int main()
{
Graph<char> g;
g.add_vertex('A');
g.add_vertex('B');
g.add_vertex('C');
g.add_vertex('D');
g.add_vertex('E');
g.add_vertex('F');
g.add_vertex('G');
g.add_edge('A', 'B', 7);
g.add_edge('A', 'D', 5);
g.add_edge('B', 'C', 8);
g.add_edge('B', 'D', 9);
g.add_edge('B', 'E', 7);
g.add_edge('C', 'E', 5);
g.add_edge('D', 'E', 15);
g.add_edge('D', 'F', 6);
g.add_edge('E', 'F', 8);
g.add_edge('E', 'G', 9);
g.add_edge('F', 'G', 11);
g.add_vertex('H');
g.add_edge('B', 'H', 9);
g.add_edge('A', 'H', 10);
g.add_edge('D', 'H', 11);
g.add_edge('A', 'H', 12);
g.remove_vertex('H');
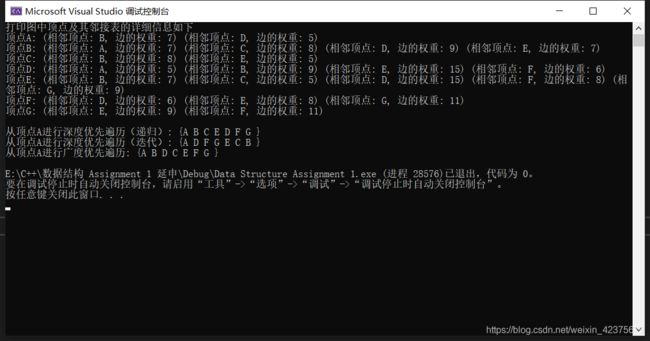
cout << "打印图中顶点及其邻接表的详细信息如下" << endl;
g.show();
cout << endl;
test02(g);
return 0;
}
}