层次分析法（Matlab实现）

基本步骤：
1.建立层次分析结构模型。常见的有目标层-准则层-方案层模型。

2.构造成对比较矩阵。常用的有1-9尺度。尺度大小取决于下层的元素个数。

3.计算权向量并作一致性检验。引入一致性指标CI，CI越大，不一致越严重。引入随机一致性指标RI。定义一致性比率CR=CI/RI。CR<0.1时，通过一致性检验。

4.计算组合权向量作组合一致性检验，组合权向量可作为决策的定量依据。方案层对目标层的组合权向量为ww*w。选择组合权向量大的元素作为输出结果。

代码：

function Example9_12
clc
a=[1,1,1,4,1,1/2
   1,1,2,4,1,1/2
   1,1/2,1,5,3,1/2
   1/4,1/4,1/5,1,1/3,1/3
   1,1,1/3,3,1,1
   2,2,2,3,3,1];%一致矩阵
[x,y]=eig(a);eigenvalue=diag(y);lamda=max(eigenvalue);
ci1=(lamda-6)/5;cr1=ci1/1.24
w1=x(:,1)/sum(x(:,1))
b1=[1,1/4,1/2;4,1,3;2,1/3,1];
[x,y]=eig(b1);eigenvalue=diag(y);lamda=eigenvalue(1);
ci21=(lamda-3)/2;cr21=ci21/0.58
w21=x(:,1)/sum(x(:,1))
b2=[1  1/4   1/5;4   1   1/2;5   2    1];
[x,y]=eig(b2);eigenvalue=diag(y);lamda=eigenvalue(1);
ci22=(lamda-3)/2;cr22=ci22/0.58
w22=x(:,1)/sum(x(:,1))
b3=[1    3  1/3;1/3   1    1/7;3   7    1];
[x,y]=eig(b3);eigenvalue=diag(y);lamda=eigenvalue(1);
ci23=(lamda-3)/2;cr23=ci23/0.58
w23=x(:,1)/sum(x(:,1))
b4=[1   1/3   5;3   1    7;1/5  1/7   1];
[x,y]=eig(b4);eigenvalue=diag(y);lamda=eigenvalue(1);
ci24=(lamda-3)/2;cr24=ci24/0.58
w24=x(:,1)/sum(x(:,1))
b5=[1   1    7;1   1    7;1/7  1/7   1];
[x,y]=eig(b5);eigenvalue=diag(y);lamda=eigenvalue(1);
ci25=(lamda-3)/2;cr25=ci25/0.58
w25=x(:,1)/sum(x(:,1))
b6=[1   7   9;1/7  1   1 ;1/9   1   1];
[x,y]=eig(b6);eigenvalue=diag(y);lamda=eigenvalue(1);
ci26=(lamda-3)/2;cr26=ci26/0.58
w26=x(:,1)/sum(x(:,1))
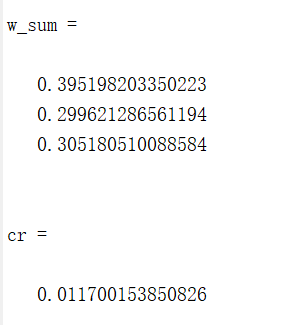
w_sum=[w21,w22,w23,w24,w25,w26]*w1
ci=[ci21,ci22,ci23,ci24,ci25,ci26];
cr=ci*w1/sum(0.58*w1)

结果如下：

可以看的出来，在CR<0.1即通过一致性检验的情况下，我们选择权重最大的作为输出结果。