机器学习(2) 感知机原理及实现
目录
- 前言
- 感知机模型
- 感知机损失函数
- 随机梯度下降法
前言
在上一篇博文机器学习(1)泛化误差上界的实现及分析中,分析了评价模型迁移学习能力的指标之一泛化误差。由Hoeffding不等式表明,在假设空间有限、样本空间有限的情况下,泛化误差是依据概率服从于泛化误差上界的,也就是说可以预估了解一个模型的可能犯错的能力。
在这篇博文中,将给出第一个二分类模型——感知机模型,并介绍在点集线性可分的条件下,可以采用随机梯度下降算法以找到一个可以将正负点集分离开的超平面。最后,给出感知机模型随机梯度下降方法及其对偶方法的C++实现。
参考文献:《统计学习方法》,李航。
感知机模型
感知机模型是最简单的、用于区分两类线性可分数据集的模型。数据集 X X X中所有的点都由每个特征的不同值唯一确定,每个数据的维数是特征的数量,记为 n n n,如果有 N N N个数据,则每个数据都记为 x i = ( x i ( 1 ) , x i ( 2 ) , x i ( 3 ) , . . . , x i ( n ) ) T , i ∈ [ 1 , N ] , x i ∈ X x_i=(x^{(1)}_i, x^{(2)}_i, x^{(3)}_i, ..., x^{(n)}_i)^{T},i\in[1,N],x_i\in{X} xi=(xi(1),xi(2),xi(3),...,xi(n))T,i∈[1,N],xi∈X;每个数据都有一个对应的类别标签,记为 y i y_i yi,我们将两种不同的数据集对应的类别分别定义为正类和负类,正类用 + 1 +1 +1来表示,负类用 − 1 -1 −1表示,即 y i ∈ Y = { + 1 , − 1 } , i ∈ [ 1 , N ] y_i\in{Y}=\{+1, -1\},i\in[1,N] yi∈Y={ +1,−1},i∈[1,N]。如果可以找到一个超平面,将正类的数据点全部划分至超平面的一侧, 而负类的数据点全部被划分至超平面的另一侧,我们称该数据集是线性可分的。
为了更好理解数据集的概念,我们给出一个例子,希望用感知机模型来区分资深程序员和新手程序员。规定每个程序员都有两个特征:代码量、工资。这里有三个程序员, x 1 = { 3 , 3 } , x 2 = { 3 , 4 } , x 3 = { 1 , 1 } x_1=\{3,3\},x_2=\{3,4\},x_3=\{1,1\} x1={ 3,3},x2={ 3,4},x3={ 1,1},如下图所示。因为资深程序员代码写的多、工资挣得多,数据集中在二维平面的右上角;新手程序员代码写得少、工资挣得少,数据集中在二维平面的左下角,这种情况下就会存在一条直线将正类划分在直线上面,且将负类数据划分在直线下面。我们称这条直线为二维空间中的超平面(hyperplane)。
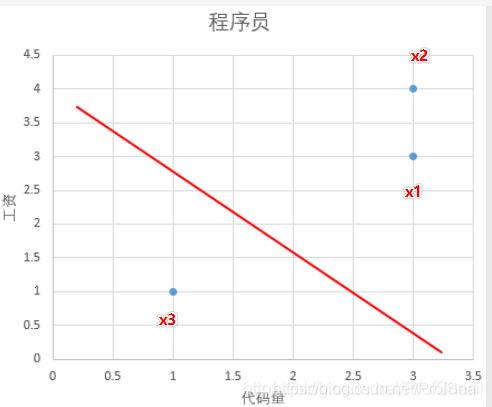
类似的,一维空间上的超平面是一个点,三维空间中的超平面就是传统意义上的平面,四维空间的超平面是一个三维组合,……,n维空间的超平面直观表现为n-1维的形象。不过大家大可不必费劲心思去想更多维度的超平面长成什么样子,因为机器学习中的每一个维度是一个特征,用于描述数据的特点,特点可以是一维的(代码量),二维的(代码量,工资),三维的(代码量,工资,发量),四维的(代码量,工资,发量,从业年龄),五维的(代码量,工资,发量,从业年龄,掌握算法数量),等等。给定维数之后,每个样本就是一个 n n n维特征组成的向量(向量指列向量),有N个数据就有N个向量。在 x = ( x ( 1 ) , x ( 2 ) , x ( 3 ) , . . . , x ( n ) ) T x=(x^{(1)},x^{(2)}, x^{(3)},..., x^{(n)})^{T} x=(x(1),x(2),x(3),...,x(n))T上定义超平面为 w ⋅ x + b = 0 w\cdot x+b=0 w⋅x+b=0,其中 w = ( w ( 1 ) , w ( 2 ) , w ( 3 ) , . . . , w ( n ) ) T w=(w^{(1)},w^{(2)}, w^{(3)},..., w^{(n)})^{T} w=(w(1),w(2),w(3),...,w(n))T同样也是n维向量, w ⋅ x w\cdot x w⋅x是两向量的内积。
因此,感知机模型的求解结果就是找到一个超平面使得正负点集可以在超平面两侧分隔开。假设数据集是线性可分的,采用梯度下降法进行优求解;如果数据集不满足线性可分性,应采用其他学习策略。特别指出的是,如上图所示,正类和负类之间的空隙可能很大,因此只需要稍微调整一下斜率或者截距,就可以得到一个全新的符合要求的超平面,这也就是说,线性可分的数据集经过一定调整,一定可以在有限次数内找到一个合适的超平面使得点集在超平面两侧;同时,这样的超平面是不唯一的,会根据初始参数选择、权值调整的策略不同而得到不同的超平面。
感知机损失函数
当感知机构成之后,就有了初始的超平面,这个超平面可能很好,让正负点集分离到平面的两侧;也可能是一个很差的超平面,让正集负集交织在了超平面的某一侧。为了表示超平面的分类性能好坏,引入损失函数的概念。损失函数满足这样的条件:
- 如果某个数据被正确分类,损失函数的数值为0。
- 如果某个数据被错误分类,损失函数的数值增加。并且分类出错的越离谱,损失函数的数值就越大;分类错误的数据越多,损失函数的数值也应该越大。
因此,定义损失函数为所有分类错误点与超平面距离之和。点到线的距离是 d = 1 ∣ ∣ w ∣ ∣ ∣ w ⋅ x + b ∣ d=\frac{1}{||w||}|w\cdot x+b| d=∣∣w∣∣1∣w⋅x+b∣,这里 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣是参数向量 w w w的 L 2 L2 L2范数。距离公式的证明参见我的另一篇博文数学基础知识(1) 点到超平面距离。为方便损失函数求导以实现梯度下降修改超平面的两个参数 w w w和 b b b,在损失函数中将距离中的正参数 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1略去。
为使输出标签为 { + 1 , − 1 } \{+1, -1\} { +1,−1},选用sign函数获得用感知机输出的预测类别。记预测的类别为 p r e d _ y i pred\_y_i pred_yi有:
p r e d _ y i = s i g n ( f ( x ) ) = s i g n ( w ⋅ x + b ) = pred\_y_i=sign(f(x))=sign(w\cdot x+b)= pred_yi=sign(f(x))=sign(w⋅x+b)= { + 1 , i f w ⋅ x + b > 0 − 1 , i f w ⋅ x + b ≤ 0 \begin{dcases}&+1,if \text{ }w\cdot x+b>0\\&-1,if\text{ }w\cdot x +b\le0\end{dcases} { +1,if w⋅x+b>0−1,if w⋅x+b≤0
当预测成功时, p r e d _ y i = y i pred\_y_i=y_i pred_yi=yi,即 y i ( w ⋅ x + b ) > 0 y_i(w\cdot x+b)>0 yi(w⋅x+b)>0;
而预测失败时,有 p r e d _ y i = − y i pred\_y_i=-y_i pred_yi=−yi,即 y i ( w ⋅ x + b ) ≤ 0 y_i(w\cdot x+b)\leq0 yi(w⋅x+b)≤0。由于我们需要找到一个超平面使得正集、负集全部处于超平面的两侧,当出现有数据点在超平面上的时候,依然认定当前的感知机平面没有收敛,需要继续进行迭代。
因此,对于分类错误的数据点, ∣ w ⋅ x i + b ∣ = − y i ( w ⋅ x + b ) |w\cdot x_i+b| = -y_i(w\cdot x+b) ∣w⋅xi+b∣=−yi(w⋅x+b)。损失函数记为:
L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b ) L(w,b)=-\sum\limits_{x_i\in M}y_i(w\cdot x_i+b) L(w,b)=−xi∈M∑yi(w⋅xi+b), M M M为所有误分类的点集合。
随机梯度下降法
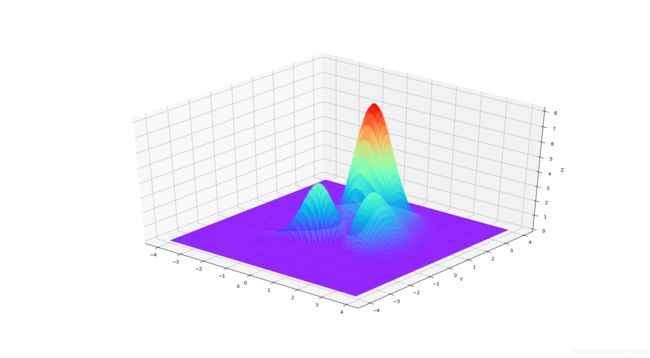
梯度下降法是机器学习过程中常用的一种优化损失函数的方法。想要了解梯度下降法,首先要感受一下什么是梯度。下面这张图像是一个峰值函数的图像,用Python绘制而成,是Matlab里面的heaps函数,我认为这张函数图像最适合于解释梯度下降法(而本文的误差函数是相反倒锥字形,选用这个图像仅仅是为了利用山峰的概念解释下山),所以在此展示出来。该函数的表达式为
- z = 3 ( 1 − x ) 2 e − x 2 − ( y + 1 ) 2 − 10 ( x 5 − x 2 − y 5 ) e − x 2 − y 2 − 1 3 e − ( x + 1 ) 2 − y 2 ) \displaystyle{z=3(1-x)^2e^{-x^2-(y+1)^2}-10(\frac{x}{5}-x^2-y^5)e^{-x^2-y^2}-\frac{1}{3}e^{-(x+1)^2-y^2)}} z=3(1−x)2e−x2−(y+1)2−10(5x−x2−y5)e−x2−y2−31e−(x+1)2−y2)
图像的绘制方法参见我的另一篇博文Python-绘制峰值图像。有了这张图像,我们就能够直观的感受到什么是梯度下降法了。
思来想去,我琢磨出了这样一句话:假设我们攀爬在一座由误差堆积而成的山峰之上,山峰之下是正确坦荡的平原。我们本应走在坦荡的平原大道之上,却误打误撞错攀上了误差的高峰。为了尽快使生活回归康庄大道,我们不得不选择一条此刻最快的下山之路。这座山峰是由一次次错误的选择堆砌而成,矫正过去犯下的错误,而又不至于矫枉过才是我们当下的选择。 我用了一段形而上的语言来总结随机梯度下降法的思路,下面我解释一下刚刚的这段话。
我们攀爬在一座由误差堆积而成的山峰之上,山峰之下是正确坦荡的平原。我们本应走在坦荡的平原大道之上,却误打误撞错攀上了误差的高峰。
根据损失函数的定义,损失函数的数值是由逐个误差点积累而成的数值,我们将这种积累过程看做造山一样,认为误差会形成一座大大山;而当误差值为0的时候,就是感知机模型收敛的时候,产生了一个超平面使得正类样本和负类样本均匀的各自分布在了超平面的两侧,这就是所说的“平原”。
为了尽快使生活回归康庄大道,我们不得不选择一条此刻最快的下山之路。
对于之前的损失函数 L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b ) L(w,b)=-\sum\limits_{x_i\in M}y_i(w\cdot x_i+b) L(w,b)=−xi∈M∑yi(w⋅xi+b)而言,样本点已经给定的条件下,视 x i , y i x_i,y_i xi,yi为常量,造成损失函数增大减小的是损失函数中变量的 w , b w,b w,b。这时用到了函数梯度的概念。关于梯度,参见我的另一篇博客数学基础知识(2) 梯度和方向向量。