Shader带你走进科技感十足的 “泰森多边形”
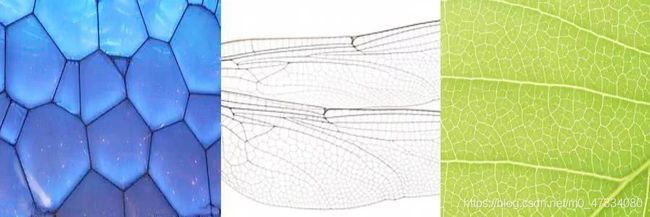
在生活中我们经常会看到一些基于泰森多边形的设计,如北京奥运会的水立方。在自然界中,泰森多边形更是随处可见,比如:蜻蜓的翅膀、树叶微观肌理等。那么我们该如何利用shader将其实现呢?
一、实现方法
1.1 什么是泰森多边形?
开始之前,我们先来了解一下泰森多边形的特征:
a. 每个泰森多边形内仅含有一个离散点数据
b. 泰森多边形内的点到相应离散点的距离最近
c. 位于泰森多边形边上的点到其两边的离散点距离相等
1.2 在shader中的实现方法
由其特征可知,我们需要先设置一组离散点,然后计算每一个像素与最近离散点的距离,也就是说我们需要遍历每个离散点,计算他们到当前像素点的距离,并把最近的那个距离保存下来。
伪代码如下:
float min_dist = 1.0;
for (int i = 0; i < TOTAL_POINTS; i++) {
float dist = distance(uv, points[i]);
min_dist = min(min_dist, dist);
}
当我们设置5个离散点,并把min_dist赋值给gl_FragColor时,就会得到类似下图的效果:
二、优化
上面的方法有些缺点,即当离散点数比较多时,我们虽然可以用for循环和数组来完成上述功能,但是遍历很多实例会显著降低着色器的性能,此外一个一个设置离散点也比较麻烦。
2.1 如何保证着色器的性能
保证着色器性能的方法就是把空间分割成网格。每个网格对应一个离散点,为避免网格交界区域的偏差,我们需要计算像素点到相邻网格中离散点的距离。每个像素点只需要计算到九个离散点的距离,即它所在的网格的离散点和相邻的八个网格的离散点。
——如何分割网格?
uv坐标默认是在0到1之间,如果我们把uv乘以一个系数,这样在0到1之间的图形就会重复生成网格。
a. 把uv乘以5,把坐标等比放大5倍:uv *= 5.0
b. 使用fract()函数单位化变量,使之在0.0到1.0之间:vec2 f_uv = fract(uv)
c. 使用floor()函数对uv取整,就知道是在哪个网格了:vec2 i_uv = floor(uv)
——计算最短距离
如何计算像素点到相邻网格中随机离散点的距离?从网格坐标来说,就是x坐标从-1(左)到1(右),y坐标从 -1(下)到1(上),一共9 个网格的3x3区域可以用两个 for 循环遍历:
伪代码如下:
for (int y= -1; y <= 1; y++) {
for (int x= -1; x <= 1; x++) {
vec2 neighbor = vec2(float(x),float(y));
vec2 diff = neighbor + point - f_uv;
float dist = length(diff);
min_dist = min(min_dist, dist);
}
}
2.2 随机构造离散点
我们知道可以通过把正弦函数打散成小片段来得到一些伪随机数。把sin(x)的值乘以大点的数,就无法区分sin波了,其小数部分的粒度将sin的循环变成了伪随机的混沌。y=fract(sin(x)*10000.0),会生成一个伪随机数,这就意味着输入相同的x值总会返回相同的值。我们如果把i_uv做为参数传入,这样每个网格内的离散点位置就都不一样了。但我们需要将一个二维向量转换为一个浮点数。最简单的就是与另一个向量进行点乘,其会返回一个0.0到1.0之间的值,通过以下随机函数我们能得到下面的图形。
伪代码如下:
float random (vec2 st) {
return fract(sin(dot(st.xy,vec2(1,10)))*10000.);
}
void main(){
precision mediump float;
float rnd = random(i_uv);
gl_FragColor = vec4(vec3(rnd),1.0);
}
我们可以通过调整所点乘的向量和系数来得到合适的效果。
2.3 最终效果
综上可得出如下效果:
三、进一步探索
这个算法还可以从离散点而非像素点的角度理解。算法可以表述为:每个离散点向外扩张生长,直到它碰到其它扩张的区域。这反映了自然界的生长规则——生命的形态是由内部扩张,并由生长力量和限制性的外部力量共同决定的。
我们可以对其展开进一步探索以创造出更多有趣的用法:
a. 修改缩放空间
b. 想办法让离散点动起来
c. 使用其它计算代替min_dist = min(min_dist, dist)。例如min_dist = min(min_dist, min_dist*dist)
讲了这么多,那么这种效果在汽车领域该如何应用呢?其实上文中的动效,我们可以把它做成车机背景,是不是很有科技感?当然其应用并不仅限于此。更多的应用还等着大家一起去挖掘和探索。