第八届“图灵杯”NEUQ-ACM程序设计竞赛个人赛（同步赛）(部分)

第八届“图灵杯”NEUQ-ACM程序设计竞赛个人赛（同步赛）

c 上进的小凡

分析：
这个子数组气死我了，我一开始是以为跟那种子序列一样的！！可恶！！气死我了！！它这个必须是连续的。比如样例中，{1，2，3}是子数组，而{1，3}不是。我们可以利用一个数组br[i]来记录以ar[i]为结尾的子数组的个数。因为子数组是连续的那么我们只需要判断ar[i]与ar[i - 1]的关系。然后大体是这样一个关系

	if(ar[i] >= ar[i - 1])	br[i] += br[i - 1] + 1;
	else	br[i] = 1;//子数组元素为1时，也是nice的

最后把br[i]全加起来即可
AC代码：

#include 

using namespace std;
typedef long long ll;

int ar[100050];
int n;
ll br[100050], ans;

int main()
{
     
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)     scanf("%d", &ar[i]);
    br[1] = 1;
    ans = 1;
    for(int i = 2; i <= n; ++i)
    {
     
        if(ar[i] >= ar[i - 1])  br[i] += br[i - 1] + 1;
        else    br[i] = 1;
        ans += br[i];
    }

    printf("%lld\n", ans);
    return 0;
}

D Seek the Joker I

D题和E题都是博弈论的模板题


分析：
比较简单的博弈问题，找到必胜态必败态即可
AC代码:

#include 

using namespace std;

int t, n, k;

int main()
{
     
    scanf("%d", &t);

    while(t--)
    {
     
        scanf("%d %d", &n, &k);
        if(n % (k + 1) == 1)    cout << "ma la se mi no.1!\n";
        else    cout << "yo xi no forever!\n";
    }
    return 0;
}

E Seek the Joker II

分析：
实质还是一个取石子游戏，有两堆石子，每次可以从任意堆中取任意个（大于0），也可以从两堆中取相同个（大于0），谁最后拿光谁赢了
AC代码：

#include 

using namespace std;

int tt, nn, x;
int a, b, t;
int n, m;
double r, c;

int main()
{
     
    scanf("%d", &tt);

    r = (sqrt(5.0) + 1) / 2;
    while(tt--)
    {
     
        scanf("%d %d", &nn, &x);
        n = x - 1;
        m = nn - x;
        a = max(n, m);
        b = min(n, m);
        c = double(a - b);
        t = (int)(r * c);
        if(t == b)  printf("ma la se mi no.1!\n");
        else        printf("yo xi no forever!\n");
    }
    return 0;
}

H 数羊

分析：
n,m >= 1是不好处理，通过手算3个样例，可以发现

	if(n >= 1 && m == 1)	ans = 2 * n;
	if(n >= 1 && m == 2)	ans = 2的n次方（快速幂取模）

快速幂模板
AC代码：

#include 
#include 

using namespace std;
typedef long long ll;
typedef unsigned long long ull;

int t;
ll n, m;

ll pow_mod(ll a, ll n, ll m)
{
     
    ll ans = 1;
    a %= m;
    while(n)
    {
     
        if(n & 1)
        {
     
            ans = (ans * a) % m;
        }
        a = (a * a) % m;
        n >>= 1;
    }
    return ans;
}


ll A(ll n, ll m)
{
     
    if(n == 1 && m == 0)    return 2;
    else if(n == 0 && m >= 0)   return 1;
    else if(n >= 2 && m == 0)   return n + 2;
    else if(n >= 1 && m >= 1)
    {
     
        if(m == 1)  return n * 2;
        else        return pow_mod(2, n, 998244353);
    }
    return 0;
}

int main()
{
     
    scanf("%d", &t);

    while(t--)
    {
     
        scanf("%lld %lld", &n, &m);
        printf("%lld\n", A(n, m));
    }
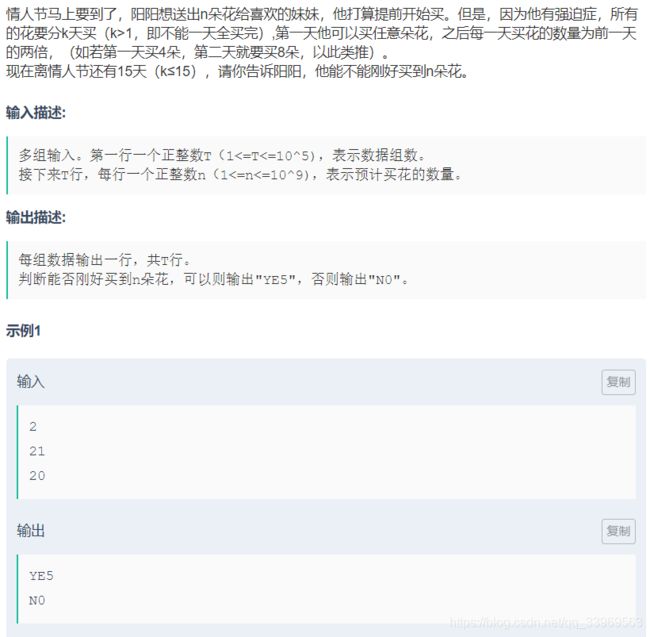
    return 0;
}

I 买花

分析：
因为之后的每一天都是前一天的2倍，所以买花总数是第一天的3， 7， 15…倍，即2^n 的前缀和倍，也等于2^n - 1倍（等比数列前n相和？）
还有就是这个鬼题输出不是YES和NO是YE5和N0；一个5一个数字0…
AC代码：

#include 

using namespace std;

int t, n;
bool flag;

int main()
{
     
    cin >> t;

    while(t--)
    {
     
        scanf("%d", &t);
        flag = 0;

        for(int i = 2; i <= 15; ++i)
        {
     
            if(n % ((1 << i) - 1) == 0)
            {
     
                flag = 1;
                printf("YE5\n");
                break;
            }
        }

        if(!flag)   printf("N0\n");
    }
    return 0;
}