【leetcode周赛】前缀检查，定长子串的元音数，二叉树回文路径，最大点积

2020/05/24 第190 场周赛

引言

没参加，但是赛后a了四道题，这次的周赛相对简单，赛后全a的有500人。

简单题

前缀检查
没啥多说的，就善用str.split()函数还是很关键的。

中等题：

1. 定长子串元音数：滑动窗口的思路，很简单
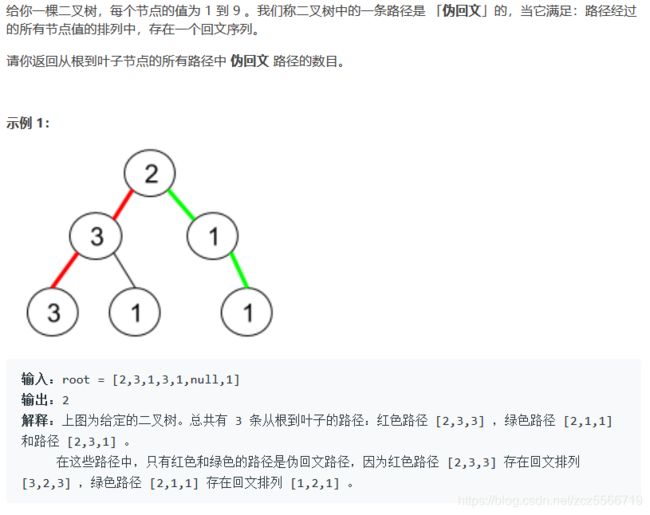
2. 二叉树中的伪回文路径：二叉树的dfs题目，可以学习下。

还是考虑迭代和递归两种思路，我写的是dfs递归的思路，题解有人给出了不错的迭代思路。

递归思路比较明确，dfs进行搜索，题目给出节点的数值最多是1-9，因此直接利用一个数组进行记录，对于回文串核心是最多只有一个数字出现奇数次，因为我们关系的只是最后每个数字出现的次数的奇偶。而异或计算可以很好的满足这个要求。

class Solution:
    def pseudoPalindromicPaths (self, root: TreeNode) -> int:
        
        # 判断数组是否最后只有最多一个1
        def isvalid(dic):
            ans = 0
            for i in range(10):
                if dic[i] != 0:
                    ans += 1
                    if ans > 1:
                        return False
            return True
        
        def dfs(root, dic):
            dic[root.val] ^= 1
            if not root.left and not root.right:
                if isvalid(dic):
                    self.cur += 1
                return 
			## 这里是个很重要的细节，需要格外的注意
            if root.left:
                dfs(root.left, dic[:])
            if root.right:
                dfs(root.right, dic[:])

        if not root:
            return 0 
        self.cur = 0
        dic = [0]*10
        dfs(root, dic)
        return self.cur

注意在函数传参时的细节问题，由于python规定参数传递都是传递引用，也就是传递给函数的是原变量实际所指向的内存空间，修改的时候就会根据该引用的指向去修改该内存中的内容，所以按道理说我们在函数内改变了传递过来的参数的值的话，原来外部的变量也应该受到影响。

但是上面我们说到了python中有可变类型（list, dict）和不可变类型(int, string, float, tuple)，这样的话，当传过来的是可变类型 (list, dict)时，我们在函数内部修改就会影响函数外部的变量。而传入的是不可变类型时在函数内部修改改变量并不会影响函数外部的变量，因为修改的时候会先复制一份再修改。因此我们在传入可变对象时，需要传复制进去

另外是迭代的方法，

class Solution:
    def pseudoPalindromicPaths (self, root):
        def isvalid(dic):
            ans = 0
            for i in range(10):
                if dic[i] != 0:
                    ans += 1
                    if ans > 1:
                        return False
            return True
        
        if not root:
            return None
        self.ans = 0
        dic = [0]*10
        stack = [(dic, root)]
        while stack:
            dic, node = stack.pop()
            dic[node.val] ^= 1
            if not node.left and not node.right:
                if isvalid(dic):
                    self.ans += 1
            if node.right:
                stack.append((dic[:], node.right))
            if node.left:
                stack.append((dic[:], node.left))
                
        return self.ans

核心思路，每次存储时候先存右侧点，再存左侧点，这样可以保证栈的先入后出原则，从最左侧开始进行计算。

困难题

两个子序列的最大点积

非常类似编辑距离的一道题目，状态dp[i][j]表示nums1[:i] nums2[:j]能够得到最优解。

转移公式：dp[i][j] = max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]+nums1[i]*nums2[j], nums1[i]*nums2[j]) 这里一定要考虑完全状态。

另外就是初始0的设计，分别写出dp[0][0], dp[i][0], dp[0][i]。

class Solution:
    def maxDotProduct(self, nums1: List[int], nums2: List[int]) -> int:
        m = len(nums1)
        n = len(nums2)
        dp = [[float('-inf')]*n for _ in range(m)]
        dp[0][0] = nums1[0]*nums2[0]
        for i in range(1,m):
            dp[i][0] = max(nums1[i]*nums2[0], dp[i-1][0])
        for i in range(1,n):
            dp[0][i] = max(nums2[i]*nums1[0], dp[0][i-1])
        for i in range(1,m):
            for j in range(1,n):
                dp[i][j] = max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]+nums1[i]*nums2[j], nums1[i]*nums2[j])
        return dp[i][j]