吴恩达机器学习作业代码（python）

吴恩达机器学习作业Python版

主要记录自己学习机器学习的过程，以及自己看别人代码时不懂或者疑惑的地方，代码主要参考Cowry5作者的代码，原作者代码和讲解更为详细，本文章如有不好的地方，还请去浏览大神的原文章(https://blog.csdn.net/Cowry5)

线性回归（一）

单变量线性回归

题目要求：自己实现单变量线性回归，以预测食品卡车的利润

1. 导入数据：

import numpy as np
import pandas as pd

#读取文件
data= pd.read_csv("ex1data1.txt",header= None,names=['population','profit']) 
#pandas读取文件时，如未指定，会默认将第一列认为是标题，所以此处要使header=None
data.head()
print("data的维度为：")
print(data.shape,"\n") #检查维度，期待输出（97，2）

2. 变量初始化：
   根据吴恩达老师所讲，为便于计算，我们在矩阵最前列加入全“1”列，然后取矩阵前两列为x（输入矩阵），最后一列为y（输出矩阵）

data.insert(0,'ones',1)
x=data.iloc[:,:-1].values
y=data.iloc[:,-1].values #.values方法即为将数据转化为矩阵形式
theta=np.zeros(x.shape[1])
print("x,y,theta的维度分别为:")
print(x.shape,y.shape,theta.shape,"\n") #检查维度，期待输出（97，2），（97，），（2，）
#插入全1列便于后续矩阵计算， 取读取数据的前两列为x矩阵（即为输入矩阵),最后一列为y矩阵（输出矩阵）

3. 定义代价函数

#定义代价函数
def calculateCost(x,y,theta):
    cost=np.sum((x@theta-y)**2)/(2*len(x)) #@为矩阵乘法符号
    return cost

4. 定义梯度下降函数

#定义梯度下降函数
def gradient(x,y,a,theta): #a为学习率，数值越小，计算越慢，结果越精确，但不宜过小，也不宜过大
    tmp=np.zeros(x.shape[1])
    i=1
     #Cowry5大神的方法为取1000次计算后的结果为最终结果
     #但我觉得那样数据可能不够精确，所以我定义一个永真循环
     #一直计算，直至theta不在发生变化，打破循环
    while(True):
        tmp = theta
        theta = theta - a * (1 / len(x)) * x.T @ (x @ theta - y)
        if((tmp==theta).all()):
            print("calculation is done!")
            print("计算次数为：",i,"次\n")
            break
        i+=1
    return theta

5. 调用方法，输出结果：

theta=gradient(x,y,0.01,theta)
print("结果显示：")
print("最终theta为：",theta)
print("最终最小代价为：",calculateCost(x,y,theta))

6. 最终结果输出

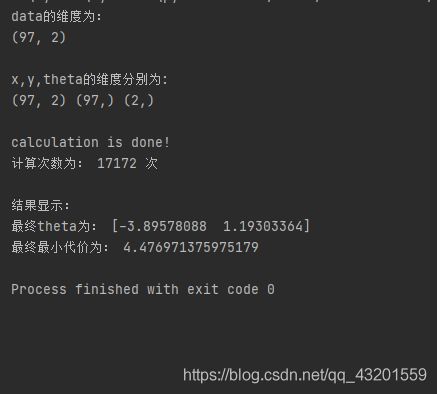
相比于计算1000次得到的最终代价：4.515955503078914，永真循环计算得到的结果更为精确。

注：最后放上整个文件的连接，里面有完整代码和数据，谢谢大家！ （^ __ ^）

链接1：csdn资源

链接2：百度云网盘
提取码：hhnb
复制这段内容后打开百度网盘手机App，操作更方便哦