AI学习笔记（八）深度学习与神经网络、推理与训练

深度学习与神经网络

神经网络

什么是神经网络

感知器：
1、外部刺激通过神经末梢，转化为电信号，转导到神经细胞（又叫神经元）
2、无数神经元构成神经中枢
3、神经中枢综合各种信号，做出判断
4、人体根据神经中枢的指令，对外部刺激做出反应。

生物神经网络的基本工作原理：
一个神经元的输入端有很多树突，主要从来接收输入信息的。输入信息经过突触处理，将输入的信息累加，当处理后的输入信息大于某一个特定的阈值，就不会吧信息通过轴突传输出去，这是神经元被刺激。相反，当处理后的输入信息小于阈值时，神经元就处于抑制状态，他不会像其他神经元传递信息。或者传递的信息很少。
人工神经网络分为两个阶段：
1、接受来自其他n个神经元传递过来的信号，这些输入信号与相应的权重进行加权就和传递给下个阶段。（预激活阶段）
2、把预激活的加权结果传递给激活函数。

人造神经元

输入：$x_1,x_2,x_3$
输出：Output
简化模型：约定每种输入只有只有两种可能为1或0
所有输入都是1，表示各种条件都成立，输出就是1；
所有输入都是0，表示条件都不成立，输出就是0
举例：
西瓜好坏？
颜色：青绿；根蒂：蜷缩；敲声：着响。—好瓜

神经网络由相互联系的神经元形成，这些神经元具有权重和网络训练期间根据错误来进行更新的偏差，目标是找到一个未知函数的近似值。其原理是受我们大脑的生理结构——互相交叉相连的神经元的启发，但与大脑一个神经元可以连接一定距离的任意神经元不同，人工神经网络具有离散的层，连接和数据传播的方向。

神经元

神经元是组成神经网络的最基本单位，它起初来源于人体，模仿人体的神经元，功能也与人体的神经元一致，得到信号的输入，进过数据处理，然后给出一个结果做出输出或者作为下一个神经元的输入。

输入是特向向量。特征向量代表的是变化的方向。或者说，是最能代表这个事物的特征的方向。权重（权值）就是特征值。有正有负，加强或抑制，同特征值一样。权重的绝对值大小，代表了输入信号对神经元的影响的大小。
最简单的把这两组向量分开的方法：
$ax+by+c=0\to y=kx+b\to y=wx+b$
把上式推广到n维空间：
$\to h=a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n+a_0=0$

神经元就是当h大于0时输出1，h小于0时输出0这么一个模型，它的实质就是把特征空间一切两半，认为两半分别属于两类。神经元的缺点在于智能一刀切，解决办法为多层神经网络。

• 神经网络是一种运算模型，由大量的节点（神经元）和之间相互的联结构成。
• 每个节点代表一种特定的输出函数，称为激活函数（activation function）。
• 每两个节点间的联结都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网路的记忆。
• 网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。而网络自身同城都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。
• 单层神经网络（感知器）。

多层神经网络

• 神经网络是由多个神经元组合而成，前一个神经元的结果作为后一个神经元的输入，一次组合而成。神经网络一般分为三层，第一层作为输入层，最后一层作为输出层，中间的全部是隐含层。
• 理论证明，任何多层网络可以用三层网络近似地表示。
• 一般平禁言确定隐藏层到底应该有多少个节点，在测试过程中也可以不断调整节点数以取得最优结果。
  

前馈神经网络

• 人工神经网络模型主要考虑网络链接的拓扑结构、神经元特征、学习规则等。
• 其中，前馈神经网络也称为***多层感知机***。
  

bp神经网络

• **BP网络（Back-Propagation Network）**是1986年被提出的，是一种按误差逆向传播算法训练的多层前馈网络，是目前应用最广泛的神经网络之一，用于函数逼近、模型识别分类、数据压缩和时间序列预测等。
• BP网络又称为反向传播神经网络，它是一种有监督的学习算法，具有很强的自适应、自学习、非线性映射能力，能较好地解决数据少、信息贫、不确定性问题，且不受非线性模型的限制。
• 一个典型的BP网络应该包括三层：输入层、隐藏层和输出层。各层之间全连接。同层之间无连接，隐藏层可以有多层。
  
  学习过程：
  正向传播：输入信号从输入层经过各个隐藏层向输出层传播。在输出层得到实际的响应值，若实际值与期望值误差较大，就会转入误差反向传播阶段。
  反向传播：按照梯度下降的方法从输出层经过各个隐含层并逐层不断地调整个神经元的连接权值和阈值，反复迭代，知道网络输出的误差减少到可以接受的成都，或者进行到预先设定的学习次数。
  BP算法是一个思想，它的基本思想如下：
  1、将训练集数据输入到神经网络的输入层，经过隐藏层，最后达到输出层并输出结果，这就是前向传播过程；
  2、由于神经网络的输入结果与实际结果又误差，则计算估计值与实际值之间的误差，并将该误差从输出层向隐藏层方向传播，直至传播到输入层；
  3、在方向传播的过程中，根据误差调整各种参数的值（相连神经元的权重），使得总损失函数减少。
  4、迭代上述三个步骤（即对数据进行反复训练），直到满足停止准则。

激活函数

• 激活函数是神经网络设计的一个核心单元。
• 在神经网络中，把处于在活跃状态的神经元称为激活态，处于非活跃状态的神经元称为抑制态。激活函数赋予了神经元自我学习和适应的能力。
• 激活函数的作用是为了在神经网络中引入非线性的学习和处理能力。
• 常用的激活函数（满足非线性、可微性、单调性、近似恒等性）。

激活函数的种类

优秀的激活函数：（优化器根据梯度下降优化参数）
1） 非线性：激活函数非线性时，多层神经网络可逼近所有函数
2） 可微性：优化器大多用梯度下降更新参数
3） 单调性：当激活函数是单调的，能保证单层网络的顺势函数使凸函数
4） 近似恒等性： 当参数初始化为随机小时，神经网络更稳定
激活函数输出值的范围：
1） 激活函数输出为有限时，基于梯度的优化方法更稳定
2） 激活函数输出为无限时，建议调小学习率

sigmod函数

$\{\begin{array}{l}f(x)=\frac{1}{1+e^{-x}}\\ f^{\prime }(x)=\frac{e^{-x}}{{\left(1+e^{-x}\right)}^2}\end{array}$

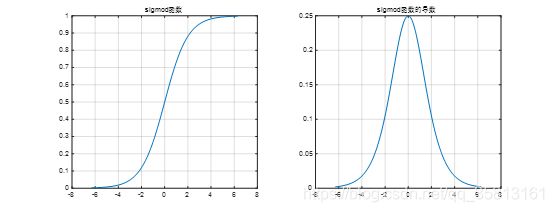
特点：
a.易造成梯度消失（梯度消失）
b.输出非0均值，收敛慢
c.幂运算复杂，计算复杂，训练时间长

tanh函数

$\{\begin{array}{l}f(x)=\frac{1-e^{-2x}}{1+e^{-2x}}\\ f^{\prime }(x)=\frac{4e^{-2x}}{{\left(1+e^{-2x}\right)}^2}\end{array}$

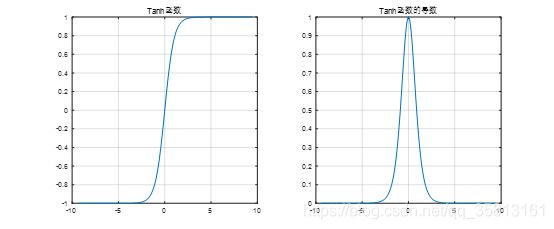
特点：
a.输出时0均值
b.易造成梯度消失
c.幂运算复杂，计算复杂，训练时间长

RelU函数（线性整流层）

$\{\begin{array}{l}f(x)=max(x,0)=\{\begin{array}{l}0x<0\\ xx⩾0\end{array}\\ f^{\prime }(x)=\{\begin{array}{l}0x<0\\ 1x⩾0\end{array}\end{array}$

优点：
a.解决了梯度消失问题（在正区间内）
b.只需判断输入是否大于0，计算速度快
c. 收敛速度远快于sigmod和tanh
缺点：
a. 输出0非均值，收敛慢
b. Dead ReIU问题，某些神经元可能不会被激活，导致相应的参数永远不能被更新
RelU起源于神经科学的研究：2001年，Dayan、Abott从生物学角度模拟处了脑神经元接收信号更精确的激活模型：

Leaky RelU函数

$\{\begin{array}{l}f(x)=max(\alpha x,0)\\ f^{\prime }(x)=max(\alpha ,1)\end{array}$

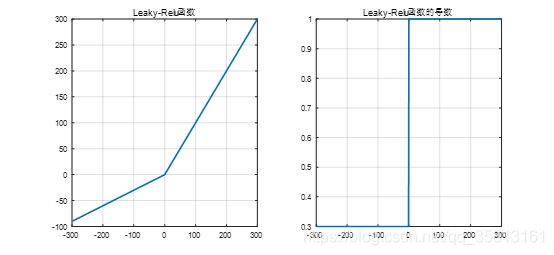
特点：
理论上来讲，Leaky Relu有Relu所有的有点，外加不会有Dead Relu问题，但是在实际操作中，并没有完全证明其比Relu好

神经元系数

ReLU函数其实是分段性函数，把所有的负值都变为0，而正值不变，这种操作被称为单侧抑制。
正因为有了这种单侧抑制，才使得神经网络中的神经元也具有了系数激活性。
当模型增加N层之后，理论上ReLU神经元的激活率将降低2的N次方倍。

损失函数

损失函数用于描述模型预测值与真实值的差距大小。一般有两种常见的算法——均值平方差（MSE）和交叉熵（cross entropy）。

• 均值平方差（Mean Squared Error，MSE），也称均方差：
  $$MSE={\sum }_{i=1}^n\frac{1}{n}(f{(x_i)-y_i)}^2$$
• 交叉熵（cross entropy）也是loss算法的一种，一般用在分类问题上，表达意思为预测输入样本属于哪一类的概率。值越小，代表预测结果越准。（y代表真实值分类（0或1），a代表预测值）：
  $$C=-\frac{1}{n}\underset{x}{\sum \left[y\ln a+(1-y)\ln (1-a)\right]}$$
  损失函数的选取取决于输入标签数据的类型：
  1、如果输入的实数、无界的值，顺势函数使用MSE。
  2、如果输入标签是位矢量（分类标志），使用交叉熵会更合适。

学习率

学习率是一个重要的超参数，它控制着我们基于损失梯度调整神经网络权值的速度。
学习率越小，我们沿着损失梯度下降的速度越慢。
从长远来看，这种谨慎慢行的选择可能还不错，因为可以避免错过任何局部最优解，但它也意味着我们要花更多的时间来收敛，尤其是如果我们处于曲线的至高点。

深度学习

张量tensor

• 任何算法得意运行，都必须依靠特定的数据结构，而用于将各种数据统一封装并输入网络模型的数据结构叫tensor，也就是张量。张量在不同的情况下存有不同的形式。
• 张量一大特征是维度，一个0维张量就是一个常量。在Python中，一个张量的维度可以通过读取它的ndim属性来获取。（我们常用的数组就等价于一维张量，一个二维数组就是一个二维张量）
• 所谓n维张量，其实就是一维数组，数组中的每个元素都是n-1维张量，由此可见，3维张量其实就是一个一维数组，数组中的每个元素就是2维数组。
• 一个n维张量经常用一组数据来表示例如下面的3维张量，它可以用（3,2,2)这组数据结合来表示，一个张量是几维度，那么括号里面就有几个数字。
  

设计神经网络

1、使用神经网络训练数据之前，必须确定神经网络层数，以及每层单元的个数
2、特征向量在被传入输入层时通常要先标准化到0~1之间（为了加速学习过程）
3、离散型变量可以被编码成每一个输入单元对弈一个特征量可能赋的值
比如：特征A可能取$(a_0,a_1,a_2)$，可以使用3个输入单元来代表A。
如果$A=a_0$，那么代表$a_0$的单元值就取1，其他取0；
如果$A=a_1$，那么代表$a_1$的单元值就取1，其他取0，以此类推；
4、神经网络既可以用来做分类（classification）问题，也可以解决回归（regression）问题
（1）对于分类问题，如果是2类，可以用一个输出单元表示（0和1分别代表2类）；如果多于2类，则每一个类别用一个输出单元表示
（2）没有明确的规则来设计最好有多少个隐藏层，可以更具实验测试和误差以及精度来实验并改进。
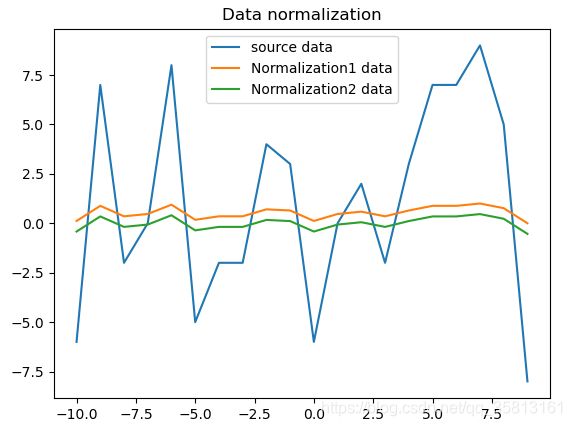
标准化代码如下：

import numpy as np
import matplotlib.pyplot as plt


def Normalization1(x):
    """
    归一化（0~1）
    x_=(x−x_min)/(x_max−x_min)
    """
    return [(float(i) - min(x)) / float(max(x) - min(x)) for i in x]


def Normalization2(x):
    """
    归一化（-1~1）
    x_=(x−x_mean)/(x_max−x_min)
    """
    return [(float(i) - np.mean(x)) / (max(x) - min(x)) for i in x]


def z_score(x):
    """
    标准化
    x∗=(x−μ)/σ
    """
    x_mean = np.mean(x)
    s2 = sum([(i - np.mean(x)) * (i - np.mean(x)) for i in x]) / len(x)
    return [(i - x_mean) / s2 for i in x]


l = np.random.randint(-10, 10, size=20)
n1 = Normalization1(l)
n2 = Normalization2(l)
x = list(range(-10, 10))
plt.plot(x, l, label='source data')
plt.plot(x, n1, label='Normalization1 data')
plt.plot(x, n2, label='Normalization2 data')
plt.legend(loc='best'), plt.title('Data normalization')
plt.show()

结果如下：

对隐藏层的感性认知

让我们从一个问题开始，假设区分一下三证图片哪个是人脸，也就是人脸识别，神经网络模型怎么建立呢？为了简单起见，输入层的每个节点代表图片的某个像素，个数为像素点的个数，输出层简单地定义为一个节点，表示“是”还是“不是”。

那么隐含层怎么分析呢？我们先从感性地角度认识这个人脸识别问题，试着将这个问题分解为一些子问题，比如：

• 在上方有头发吗？
• 在左上、右上各有一个眼睛吗？
• 在中间有鼻子吗？
• 在下方中间位置有嘴巴吗？
• 在左右两侧有耳朵吗？
• $\cdots$
  假设对以上这些问题的回答，都是“yes”，或者大本分都是“yes”，那么可以判定人脸，否则不是人脸。

深度神经网络与深度学习

• 传统的神经网络发展到了多隐藏层的情况。
• 具有多个隐藏层的神经网络被称为深度神经网络，基于深度神经网络的机器学习研究称之为深度学习。
• 若谷需要细化和区分别，那么，深度神经网络可以理解为对传统多层网络进行了结构、方法等方面的优化。
  
  深度学习，就是多层人工神经网络。
  
  图像识别：像素->边缘->纹理->图形->局部->物体
  文字识别：字符->词->词组->子句->句子->故事
  数据规律推动深度学习进步
  
  

推理与训练

监督学习与非监督学习

**Supervised Learning有监督学习：**输入的数据被称为训练数据，一个模型需要通过一个训练过程，在这个过程中进行预期判断，如果错误了再进行修正，训练过程一直持续到基于训练数据达到预期的精确性。其关键方法是分类和回归，算法是逻辑回归（Logistic Regression）和BP神经网络（Back Propagation Neural Network）。
**Unsupervised Learning无监督学习：**没有任何训练数据，基于没有标记的输入数据采取推到结构的模型，其关键方式是关联规则学习和聚合，算法有Apriori算法和K-Means。

优化和泛化

深度学习的根本问题是优化和泛化之间的对立。

• 优化（optimization）是指调节模型以在训练数据上得到最佳性能（及机器学习中的学习）。
• 泛化（generalization）是指训练好的模型在前所未见的数据上的性能好坏。

泛化能力分类

• 欠拟合：模型没有能够很好的表现数据的结构，而出现的拟合度不高的情况，模型不能再训练集上获得足够低的误差；
• 拟合：测试误差与训练误差差距较小；
• 过拟合：模型过分的拟合训练样本，但对测试赝本预测准确率不高的情况，也就是说模型的泛化能力差。训练误差和测试误差之间的差距太大。
• 不收敛：模型不是根据训练集训练得到的。
  

过拟合

• 过拟合指的是给定一堆数据，这对数据带有噪声，利用模型取拟合这对数据，可能会把噪声数据也过拟合了。
• 一方面会造成模型比较复杂
• 另一方面，模型的泛化能力太差了，遇到了新的数据，用所得到的过拟合模型，正确率很差。

过拟合的原因

1、建模样本选取了错误的选样方法、样本标签等，或样本数量太少，所选取的样本数据不足以代表预定的分类规则；
2、样本的噪音干扰过大，使得及其将部分噪音认为是特征从而扰乱了预设的分类规则
3、假设的模型无法合理存在，或者说是无法达到假设成立的条件
4、参数太多导致模型复杂度过高
5、对于神经网络模型：a）对样本数据可能存在分类决策面不唯一，随着学习的进行，BP算法使权重可能收敛过于复杂的决策面；b）权重学习迭代次数足够多，拟合了训练数据中心的噪声和训练样例中没有代表性的特征。

过拟合的解决办法

1、减少特征：删除与目标不相关的也正，如一些特征选择方法
2、Early stopping
3、更多的训练样本
4、重新清洗数据、数据增强
5、Dropout

Eearly Stopping

• 在每一个Epoch结束时，计算validation data的accuracy，当accuracy不再提高时，就停止训练；
• 那么该做法的一个重点便是怎样才认为validation accuracy不再提高了呢？并不是说validation accuracy一降下来边认为不再提高了，因为可能经过这个Epoch后，accuracy降低了，但是随后的Epoch又让accuracy上去了，所以不能根据一两次的连续降低就判断不在提高。
• 一般的做法是，在训练过程中，记录到目前为止最好的validation accuracy，当连续10次Epoch（或者更多次）没有达到最佳accuracy时，则可以认为accuracy不再提高了，此时便可以停止迭代了；
• 这种策略也称为“No-improvement-in-n"，n即Epoch的次数，可以根据实际情况取，如10、20、30

Dropout

在神经网络中，dropout方法是通过修改神经网络本身结构来实现的：
1、在训练开始是，随机删除一些（可以设定为1/2，也可以为1/3，1/4等）隐藏层神经元，即认为这些神经元不存在，同时保持输入层与输出层神经元个数不变。（相应权重变为0）
2、然后按照BP学习算法对ANN中的参数进行学习更新（虚拟连接的单元不更新，因为认为这些神经元被临时删除了）。这样一次迭代更新便完成了。下一次迭代中，同样随机删除一些神经元，与上次不一样，做随机选择。这样一直进行，直至训练结束。
Dropout方法是通过修改ANN中隐藏层的神经元个数来防止ANN的过拟合。

为什么Dropout能够减少过拟合
1、Dropout是随机选择忽略隐藏层节点，在每个批次的训练过程：由于每次随机忽略的隐藏层节点都不同，这样就使每次训练的网络都是不一样的，每次训练都可以当做一个“新”模型；
2、隐藏节点都是以一定概率随机出现，因此不能保证每2个隐含节点每次都同时出现。这样权值的更新不再依赖有固定关系隐含节点共同作用，阻止了某些特征仅仅在其他特定特征下才有效果的情况
Dropout是一个非常有效的神经网络平均方法，通过训练大量的不同的网络，来平均预测概率。不同的模型在不同的训练集上训练（每个epoch的训练数据都是随机选择），然后在每个模型用相同的权重来“融合”。

• 经过交叉验证，隐藏节点dropout率等于0.5的时候效果最好。
• dropout也可以被用作一种添加噪声的方法，直接对input进行操作，输入层设为更接近于1的数，使得输入变化不会太大
• dropout的缺点在于训练时间是没有dropout网络的2-3倍。

数据集的分类

数据集可以分为：

• 训练集：实际训练算法的数据集；用来计算梯度，并确定每次迭代中网络权值的更新；
• 验证集：用于跟踪其学习效果的数据集；是一个指示器，用来表明训练数据点之间所形成的的网络函数发生了什么，并且验证集上的误差值在整个训练过程中都被检测；
• 测试集：用于产生最终结果的数据集。
  为了让测试集有效反映网络的泛化能力：
  1、测试集绝不能以任何形式用于训练网络，即使适用于同一组备选网络中挑选网络。测试集只能在所有的训练和模型选择完后使用；
  2、测试集必须代表网络使用中涉及的所有情形。

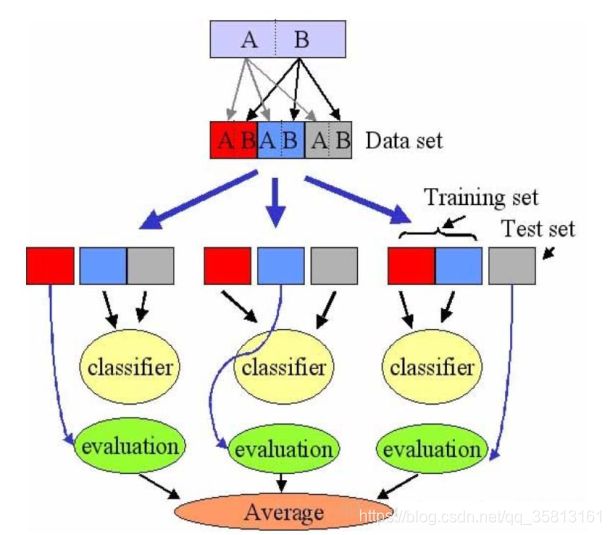
交叉验证

这里有一堆数据，我们把它切成3个部分（当然还可以更多）
第一部分做测试集，二三部分做训练集，算出准确度；
第二部分做测试集，一三部分做训练集，算出准确度；
第三部分做测试集，一二部分做训练集，算出准确度；
之后算出三个准确度的平均值，作为最后的准确度。

深度学习的推理和训练

**训练（Training）：**一个初始神经网络通过不断的优化自身参数，来让自己变得准确。这整个过程称之为训练（Training）。
**推理（Inference）：**训练好了一个模型，在训练数据集中表现良好，但是我们的期望是它可以对以前没看过的图片进行识别。当重新拍一张图片扔进网络让网络做判断，这种图片就叫做现场数据（live data），如果现场数据的区分准确率非常高，那么证明你的网络训练的是非常好的。这个过程，称为推理（Inference）。
我们利用神经网络取解决图像分割，边界探测等问题的时候，我们的输入（假设为x），与期望的输出（假设为y）之间的关系究竟是什么？也就是$y=f(x)$中，$f$是什么，我们也不清楚，但是我们对一点很确信，那就是$f$不是一个简单的线性函数，应该是一个抽象的复杂的关系，那么利用神经网络就是去学习这个关系，存放到model中，利用得到的model去推测训练集之外的数据，得到期望的结果。
**代（Epoch）：**使用训练集的全部数据对模型进行一次完整训练，被称为“一代训练”。
**批大小（Btach size）：**使用训练集的一部分样本对模型权重进行一次方向传播的参数更新，这一小部分样本被称为“一批数据”
**迭代（Iteration）：**使用一个Batch训练对模型进行一次参数更新的过程，被称为“一次训练”（一次迭代）。每一次迭代得到的结果都会被作为下一次迭代的初始值。一个迭代=一个正向通过+一个反向通过。
$$NumberofBatches=\frac{TrainingSetSize}{BatchSize}$$
比如训练集有500个样本，$batchsize=10$，那么训练完整个样本集：$iteration=50,epoch=1$。

神经网络的训练过程

可描述为：
1、提取特征向量作为输入。
2、定义神经网络结构。包括隐藏层数，激活函数等。
3、通过训练利用反向传播算法不断优化权重的值，使之达到最合理水平。
4、使用训练好的神经网络来预测未知数据（推理），这里训练好的网络就是指权重达到最优的情况。
可描述为：
1、选择样本集合的一个样本（Ai，Bi），Ai为数据、Bi为标签（所属类别）
2、送入网络，计算网络的实际输出Y，（此时网络中的权重应该都是随机量）
3、计算D=Bi-Y（即预测值和实际值相差多少）
4、根据误差D调整权重矩阵W
5、对每个样本重复上述过程，直到对整个样本集来说，误差不超过规定范围
也可描述为：
1、参数的随机初始化
2、前向传播计算每个样本对应的输出节点激活函数值
3、计算损失函数
4、反向传播计算偏导数
5、计算梯度来进行梯度检查，以判断偏导数计算的正确性。如果正确就取消掉梯度检查。
6、使用梯度下降法或者先进的方法更新权值

参数的随机初始化

权重初始化并不是简单的随机初始化，而是一项会影响训练性能的关键一步，而且有时候会依赖于选择的激活函数。如果仅仅是权重随机初始化为一些很小的随机数，他会打破梯度更新对称性。
1、权重参数初始化从区间均匀随机取值。
2、XAvier初始化（sigmod、tanh）$W\sim U\left[-\frac{\sqrt{6}}{\sqrt{H_k+H_{k+1}}},\frac{\sqrt{6}}{\sqrt{H_k+H_{k+1}}}\right]$。
3、初始化为小的随机数（小型网络）：比如，可以初始化为均值为0，方差为0.01的高斯分布。
4、权重初始化为正态分布（relu）。
5、MSRA Filler(relu)：用均方差为0，方差为$\sqrt{\frac{4}{n_{in}+n_{out}}}$的高斯分布。
6、偏置bias的初始化，一般初始化为0。

标准化

原因：由于进行分类器或模型的建立与训练时，输入的数据范围可能比较大，同时样本中各数据可能量纲不一致，这样的数据容易对模型训练或分类器的构建结果产生影响，因此需要对其进行标准化处理，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。
其中最典型的就是数据的归一化处理，即将数据统一映射到$[0,1]$区间上。
$$y=\frac{x-min}{max-min}$$
z-score标准化（零均值归一化zero-mean normalization）

• 经过处理后的数据均值为0，标准差为1（正态分布）
• 其中$\mu$是样本的均值，$\sigma$是样本的标准差
  $$y=\frac{x-\mu }{\sigma }$$

梯度下降法

• 梯度$\nabla f=(\partial x_1\partial f;\partial f_2\partial f;\cdots \partial x_n\partial f)$指数函数关于变量x的导数，梯度的方向表示函数值增大的方向，梯度的模表示函数值增大的速率。
• 那么只要不断将参数的值向着梯度的方方向更新一定大小，就能得到函数的最小值（全局最小值或者局部最小值）。
• 一般利用梯度更新参数时会将梯度乘以一个小于1的学习率（learning rate），这是因为往往梯度的模还是比较大的，直接用其更新参数会使函数值不断波动，很难收敛到一个平衡点（这也是学习率不宜过大的原因）。
  $${\theta }_{t+1}={\theta }_t-{\alpha }_t\nabla f({\theta }_t)$$
  
  紫色部分：正确结果与节点输出结果的插值，也就是误差；
  红色部分：节点的激活函数，所有输入该节点的立案率把经过其上的信号与立案率权重做乘积后求和，再把求和结果进行激活函数运算；
  绿色部分：链路$w(jk)$前节点输出的信号值。

神经网络的训练过程实例

1、第一层是输入层，包含两个神经元：$i_1,i_2$和偏执$b_1$；
2、第二层是隐藏层，包含两个神经元：$h_1,h_2$和偏执$b_2$；
3、第三层是输出：$o_1,o_2$；
4、每条线上标的$w_i$是层与层之间连接的权重；
5、激活函数是sigmod函数；
6、用$z$表示某个神经元的加权输入和；用$a$表示某神经元的输出。

神经网络训练过程实例-Step 1 前向传播
输入层->隐藏层
神经元$h_1$的输入加权和：
$z_{h1}=w_1{i}_1+w_2{i}_2+b_1=0.15\ast 0.05+0.2\ast 0.1+0.35=0.3775$
神经元$h_1$的输出$a_{h1}$：
$a_{h1}=\frac{1}{1+e^{-z_{h1}}}=\frac{1}{1+e^{-0.3775}}=0.593269992$
同理可得，神经元$h_2$的输出$a_{h2}$:
$a_{h2}=0.596884378$
隐藏层->输出层
计算输出层神经元$o_1$和$o_2$的值：
$$\begin{gathered} z_{o1}=w_5{a}_{h1}+w_6{a}_{h2}+b_2 \\ =0.4\ast 0.593269992+0.45\ast 0.596884378+0.6=1.105905967 \end{gathered}$$
$a_{o1}=\frac{1}{1+e^{-z_{a1}}}=\frac{1}{1+e^{-1.105905967}}=0.751365069$
同理可得：
$a_{o2}=0.772928465$
前向传播的过程就结束了，我们得到的输出值是$[0.751365069,0.772928465]$，与实际值$[0.01,0.99]$相差还很远。接下来我们对误差进行反向传播，更新权值，重新计算输出。
神经网络训练过程实例-Step 2反向传播
1、计算损失函数
$E_{total}=\sum \frac{1}{2}{(target-output)}^2$
两个输出，所以分别计算$o_1$和$o_2$的损失值，总误差为两者之和：
$$\begin{gathered} E_{o_1}=\frac{1}{2}{(0.01-0.751365069)}^2=0.274811083 \\ {E}_{o_2}=\frac{1}{2}{(0.09-0.772928465)}^2=0.023560026 \\ {E}_{total}=E_{o_1}+E_{o_2}=0.274811083+0.023560026=0.298371109 \end{gathered}$$
2、隐藏层->输出层的权值更新
以权重参数$w_5$为例，如果我们想知道$w_5$对整体损失产生了多少影响，可以用整体损失对$w_5$求骗导：
$\frac{\partial E_{total}}{\partial w_5}=\frac{\partial E_{total}}{\partial a_{o1}}\ast \frac{\partial a_{o1}}{\partial z_{o1}}\ast \frac{\partial z_{o1}}{\partial w_5}$

接下来分别计算每个式子的值：
计算$\frac{\partial E_{total}}{\partial a_{o1}}$:
$$\begin{gathered} E_{total}=\frac{1}{2}{\left(targe{t}_{o1}-a_{o1}\right)}^2+\frac{1}{2}{\left(targe{t}_{o2}-a_{o1}\right)}^2 \\ \frac{\partial E_{total}}{\partial a_{o1}}=2\ast \frac{1}{2}\left(targe{t}_{o1}-a_{o1}\right)\ast (-1) \\ =-\left(targe{t}_{o1}-a_{o1}\right)=0.751365069-0.01=0.741365069 \end{gathered}$$
计算$\frac{\partial E_{total}}{\partial z_{o1}}$:
$$\begin{gathered} a_{o1}=\frac{1}{1+e^{-z_{o1}}} \\ \frac{\partial a_{o1}}{\partial z_{o1}}=a_{o1}(1-a_{o1})=0.751365069\ast (1-0.751365069)=0.186815602 \end{gathered}$$
计算$\frac{\partial z_{o1}}{\partial w_5}$:
$$\begin{gathered} z_{o1}=w_5{a}_{h1}+w_6{a}_{h2}+b_2 \\ \frac{\partial z_{o1}}{\partial w_5}=a_{h1}=0.593269992 \end{gathered}$$
最后三者相乘：
$$\begin{gathered} z_{o1}=w_5{a}_{h1}+w_6{a}_{h2}+b_2 \\ \frac{\partial E_{total}}{\partial w_5}=0.741365069\ast 0.186815602\ast 0.593269992=0.082167041 \end{gathered}$$
这样我们就算出整体损失$E_{total}$对$w_5$的偏导值。
$$\begin{gathered} z_{o1}=w_5{a}_{h1}+w_6{a}_{h2}+b_2 \\ \frac{\partial E_{total}}{\partial w_5}=-\left(targe{t}_{o1}-a_{o1}\right)\ast a_{o1}\ast (1-a_{o1})\ast a_{h1} \end{gathered}$$
针对上述公式，为了方便表达，使用${\delta }_{o1}$来表示输出层的误差：
$$\begin{gathered} {\delta }_{o1}=\frac{\partial E_{total}}{\partial a_{o1}}\frac{\partial a_{o1}}{\partial z_{o1}}=\frac{\partial E_{total}}{\partial z_{o1}} \\ =-(targe{t}_{o1}-a_{o1})\ast a_{o1}\ast (1-a_{o1}) \end{gathered}$$
因此整体损失$E_{total}$对$w_5$的偏导值可以表示为：
$\frac{\partial E_{total}}{\partial w_5}={\delta }_{o1}\ast a_{h1}$
最后更新$w_5$的值：
$w_5^{+}=w_5-\eta \frac{\partial E_{total}}{\partial w_5}=0.4-0.5\ast 0.82167041=0.35891648$
同理更新$w_6,w_7,w_8$:
$$\begin{gathered} w_6^{+}=0.408666186 \\ {w}_7^{+}=0.511301270 \\ {w}_8^{+}=0.561370121 \end{gathered}$$
2、隐藏层->隐藏层的权值更新
$rac\partial E_{total}\partial w_1=\frac{\partial E_{total}}{\partial ou{t}_{h1}}\frac{\partial ou{t}_{h1}}{\partial ne{t}_{h1}}\frac{\partial ne{t}_{h1}}{\partial w_1}=\left(\frac{\partial E_{o1}}{\partial ou{t}_{h1}}+\frac{\partial E_{o2}}{\partial ou{t}_{h1}}\right)\frac{\partial ou{t}_{h1}}{\partial ne{t}_{h1}}\frac{\partial ne{t}_{h1}}{\partial w_1}$

计算$\frac{\partial E_{total}}{\partial a_{h1}}$
$\frac{\partial E_{total}}{\partial a_{h1}}=\frac{\partial E_{o1}}{\partial a_{h1}}+\frac{\partial E_{o2}}{\partial a_{h1}}$
先计算$\frac{\partial E_{o1}}{\partial ou{t}_{h1}}$
$$\begin{gathered} \frac{\partial E_{o1}}{\partial a_{h1}}=\frac{\partial E_{o1}}{\partial a_{o1}}\ast \frac{\partial a_{o1}}{\partial z_{o1}}\ast \frac{\partial z_{o1}}{\partial a_{h1}} \\ =0.741365069\ast 0.18615602\ast 0.4=0.055399425 \end{gathered}$$
同理可得：
$\frac{\partial E_{o2}}{\partial a_{h1}}=-0.019049119$
两者相加得：
$\frac{\partial E_{total}}{\partial a_{h1}}=0.055399425-0.019049119=0.036350306$
计算$\frac{\partial a_{h1}}{\partial z_{h1}}$
$\frac{\partial a_{h1}}{\partial z_{h1}}=a_{h1}\ast (1-a_{h1})=0.593269992\ast (1-0.593269992)=0.2413007086$
计算$\frac{\partial a_{h1}}{\partial w_1}$
$\frac{\partial a_{h1}}{\partial w_1}=i_1=0.05$
最后三者相互乘：
$\frac{\partial E_{total}}{\partial w_1}=0.036350306\ast 0.2413007086\ast 0.04=0.000438568$
为了简化公式，用${\delta }_{h1}$表示隐藏层单元$h_1$的误差：
$$\begin{gathered} \frac{\partial E_{total}}{\partial w_1}=\left({\sum }_i\frac{\partial E_{total}}{\partial a_i}\frac{\partial a_i}{\partial z_i}\frac{\partial z_i}{\partial h_1}\right)\frac{\partial a_{h1}}{\partial z_{h1}}\frac{\partial z_{h1}}{\partial w_1} \\ =\left({\sum }_i{\delta }_i{w}_{hi}\right)\ast a_{h1}\ast (1-a_{h1})\ast i_1={\delta }_{h1}\ast i_1 \end{gathered}$$
最后更新$w_1$的权值：
$w_1^{+}=w_1-\eta \frac{\partial E_{total}}{\partial w_1}=0.15-0.5\ast 0.0004358568=0.149780716$
同理，更新$w_2,w_3,w_4$的权值：
$$\begin{gathered} w_2^{+}=0.19956143 \\ {w}_3^{+}=0.24975114 \\ {w}_4^{+}=0.29950229 \end{gathered}$$
这样，反向传播算法就完成了，最后再把更新的权值重新计算，不停地迭代。
在这个例子中第一次迭代之后，总误差0.298371109下降至0.291027924.
迭代10000次后，总误差为0.000035085，输出为[0.015912196,0.984065734]

用keras实现一个简单神经网络

Keras由纯pyhton编写的基于theano/tensorflow的深度学习框架。
Keras是一个高层次神经网络API，支持快速实验，能够迅速将idea转化为结果，当有如下需求时，可以优先选择Keras：
1、简易和快速的原型设计（keras具有高度模块化，极简，可扩充特性）
2、支持CNN，RNN，或二者的结合
3、无缝CPU和GPU切换

Softmax

Softmax用于多分类过程中，它将多个神经元的输出，映射到[0,1]区间内，可以看成概率来理解，从而来进行多分类。
假设有一组数据，$V$，$V_i$表示$V$中的第$i$个元素，那么这个元素的softmax值就是：
$$S_i=\frac{e^{V_i}}{{\sum }_j{e}^{V_j}}$$