轻轻松松理解Base64

前言

在开发中，Base64编码会经常使用到，平时也就是使用，没有去真正了解过Base64的原理，今天开发的时候，使用key、value的方式保存Base64编码之后的字符串，文件中的形式为key=value，但是Base64字符串本身就有等于号（=），所以，我担心这会不会出问题啊？我使用的是Properties类来保存key/value的，我发现Properties会自动对保存的字符串中出现的等于号做转义，示例如下：

weOcndflNzFLAyseO/JcBA\=\==bjWJ6o9guMCPxAjgdpF2hA\=\=

\= 就是转义的，Properties读到这两个符号的时候，会把它当成一个普通字符，所以对于：\=\== ，这里前面的两个等于号是普通字符，第三个等于号就是key/value的分隔符了，Properties会把第三个等号前面的字符当作key，后面的字符当作value，所以不会有问题。

但是我突然又想到，万一Base64的字符串里面本身就包含有反斜杠呢？这会不会导致读取出错啊，于是乎这时需要我去了解一下Base64都有哪些字符。

Base64编码基本原理

在百度百科里面就有很详细的解释，Base64，顾名思义，就是任意的内容，都可以使用64个字符来进行编码表示，如下：

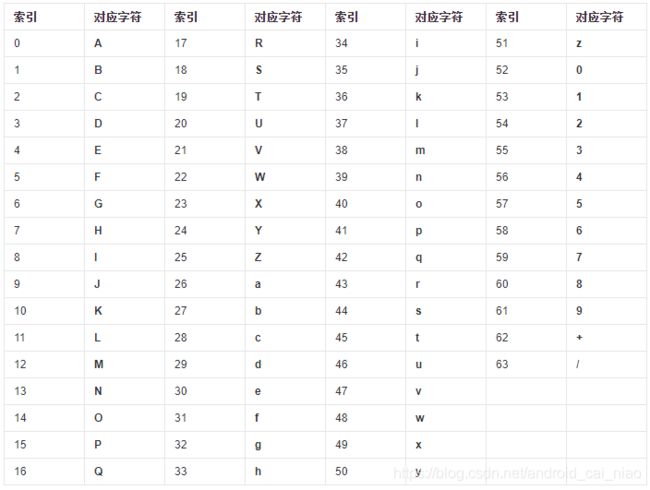
总结64个字符为：26个大写字母（A - Z）、26个小字字母（a - z）、10个数字（0 - 9）、两个字符（+ /），共64个字符。所以Base64的字符串中不会出现反斜杠等一些特殊符号，方便进行显示，且这64个符号都是可打印符号，显示肯定是没问题的。

看到这里，我在想，Base64怎么这么神奇呢？它是怎么做到64个字符就可以表示一切的呢？比如，一张图片可以用Base64表示，一段音频可以用Base64表示。。。所有的数据都可以编码为Base64，然后还可以还原回原来的内容，就是这么神奇。

当我了解了Base64的原理之后，感觉简单到不行，一点也不神奇了！其实计算机上所有的数据（文本、图片、音乐、视频等等）都是二进制，即0101010110这样的二进制数据，Base64就是把这些二进制进行编码而已，编码规则如下：

1. 每三个字节拆分成4个字节。三个字节共有24个位（3 x 8 = 24），分成4字节后，则每个字节分得原字节的6个位（24 / 4 = 6），6个位的大小正好可以表示 0 ~ 63，共64个字数，这就是Base64的由来。
2. 64个数字分别对应64个符号。
3. 字节不够的话，使用等于号填充。比如，把一个字节进行Base64编码，1字节只能分成：6个位 + 2个位，共可以组成两个字节，还差两个字节，所以需要使用两个等于号进行填充，所以，我们在看Base64的时候，经常可以在Base64字符串的最后看到有等于号，最多只可能有两个等于号，因为1个字节变成Base64就占两字节了，还差两字节就使用两等于号来填充。

下面举例说明：

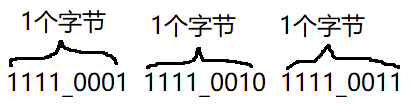
如上图，有3个字节，使用Base64对这3个字节进行编码，则Base64会把这3个字节化分成4个字节，如下：

为了美观，我们把转换后的Base64字节重新画图，如下：

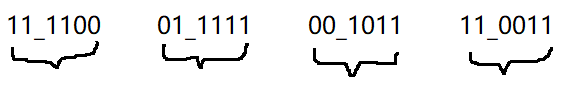
Ok，这样就把3个字节（共24位）分成了4个字节，但是计算机里的一个字节是占8个位的，所以上图中的Base64字节还需要补上两个0，以填充满8个位，如下：

到这里，Base64最核心的编码规则就了解的差不多了，可以看到，原始字节是3个字节，使用Base64编码后变成了4个字节，所以，使用Base64编码，需要的存储空间比原来多33.33%（1 / 3 = 33.33%），即按原始字节保存是保存3个字节，Base64编码后需要保存4个字节，如下图：

Base64补位规则

前面我们说了，Base64会把3个字节转换为4个字节，所以Base64的最小长度为4个字节，也就是说Base64字符串的长度最短为4个字符。这时我就想了，那如果我想编码的数据只有1个字节呢（计算机存储的最小单位为字节）？很简单，1个原始字节可以编码为两个Base64字节：分为6位 + 2位，Base64最少要4个字节，那还差两个字节，所以使用等于号填充，示例如下：

把0b0000_0100编码为Base64，结果是怎样的呢？我们先用代码运行一下结果：
（ 注：jdk1.7及以上版本可以使用0b开头表示二进制，且数值之间可以使用下划线分隔）

fun main() {
     	
    val bytes = byteArrayOf(0b0000_0100)
    println(Base64.getEncoder().encodeToString(bytes))
}

输出结果如下：

BA==

0b0000_0100对应的十进制为4，4编码为Base64后结果为：BA==，接下来，我们就一步步分解，如下：

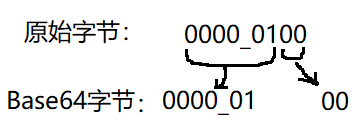
如上图，可以看到，1个原始字节分成了两个Base64字节，我们把Base64字节补齐8位（在高位补0），如下：

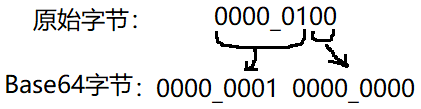
Ok，这样就把0000_0100编码为了两个Base64字节了，分别为：0000_0001、0000_0000，这两个字节对应的十进制值为1和0，然后我们到Base64符号表中查找，数字1对应的符号为B，字节0对应的符号为A。我们说Base64最少要4个字节，这里只有两个字节，所以需要使用两个等于号填充，所以最终显示结果为：BA==

Base64的变种

上面是标准的Base64，了解了原理之后，其实我们自己也可以写一个类似的编码，即使用不同的符号来表示，实现起来并不难，所以市面上也出现了不同的变种，下面引用一下百度百科的内容：

标准的Base64并不适合直接放在URL里传输，因为URL编码器会把标准Base64中的“/”和“+”字符变为形如“%XX”的形式，而这些“%”号在存入数据库时还需要再进行转换，因为ANSI SQL中已将“%”号用作通配符。

为解决此问题，可采用一种用于URL的改进Base64编码，它在末尾填充’='号，并将标准Base64中的“+”和“/”分别改成了“-”和“”，这样就免去了在URL编解码和数据库存储时所要作的转换，避免了编码信息长度在此过程中的增加，并统一了数据库、表单等处对象标识符的格式。

另有一种用于正则表达式的改进Base64变种，它将“+”和“/”改成了“!”和“-”，因为“+”,“*”以及前面在IRCu中用到的“[”和“]”在正则表达式中都可能具有特殊含义。

此外还有一些变种，它们将“+/”改为“-”或“.”（用作编程语言中的标识符名称）或“.-”（用于XML中的Nmtoken）甚至“:”（用于XML中的Name）。

验证所有Base64符号

0 ~ 63，共64个数字，分别使用64个字符来显示，那我们就来验证一下。

前面我们知道，1个字节会被分成两个字节，差两个字节用等于号填充。

0000_0100编码为Base64，首先会把前6个位（0000_01）编码为1个字节，后两位(00)也编码为1个字节，这里我就不使用后两位了，我想办法让前6位的值从0 ~ 63变化（很简单，让前6位每次加1即可），然后看结果是否正好对应上Base64中的64个字符，这样的话，结果为：XA==，其中X是未知符号，A==是固定符号，因为后两位为0，0对应的Base64符号为A，差两字节所以补两个等于号，所以A==是已知符号，接下来我们就实现前6位符号的变化，代码如下：

fun main() {
     
    var number = -0b0000_0100
    repeat(64) {
     
        number += 0b0000_0100
        val bytes = byteArrayOf(number.toByte())

        val high6Bit = number ushr 2 // 取出高6位的值
        // 索引小于10的在前面补0
        val high6BitString = "${if (high6Bit < 10) "0" else ""}$high6Bit"
        println("$high6BitString(${
       toBinaryString(high6Bit)}) : ${
       Base64.getEncoder().encodeToString(bytes)}")
    }
}

/** 将指定的十进制数转换为对应的二进制表示形式 */
private fun toBinaryString(number: Int): String {
     
    var binaryString = Integer.toBinaryString(number)
    repeat(8 - binaryString.length) {
     
        // 不够8位的在前面补0
        binaryString = "0$binaryString"
    }
    return binaryString.substring(0, 6) // 不要最后的两个0
}

为什么是加0b0000_0100，因为1是要加到前6位的位置，所以是加0b0000_0100，这样后两位永远是00，运行结果如下：

00(00000000) : AA==
01(00000100) : BA==
02(00001000) : CA==
03(00001100) : DA==
04(00010000) : EA==
05(00010100) : FA==
06(00011000) : GA==
07(00011100) : HA==
08(00100000) : IA==
09(00100100) : JA==
10(00101000) : KA==
11(00101100) : LA==
12(00110000) : MA==
13(00110100) : NA==
14(00111000) : OA==
15(00111100) : PA==
16(01000000) : QA==
17(01000100) : RA==
18(01001000) : SA==
19(01001100) : TA==
20(01010000) : UA==
21(01010100) : VA==
22(01011000) : WA==
23(01011100) : XA==
24(01100000) : YA==
25(01100100) : ZA==
26(01101000) : aA==
27(01101100) : bA==
28(01110000) : cA==
29(01110100) : dA==
30(01111000) : eA==
31(01111100) : fA==
32(10000000) : gA==
33(10000100) : hA==
34(10001000) : iA==
35(10001100) : jA==
36(10010000) : kA==
37(10010100) : lA==
38(10011000) : mA==
39(10011100) : nA==
40(10100000) : oA==
41(10100100) : pA==
42(10101000) : qA==
43(10101100) : rA==
44(10110000) : sA==
45(10110100) : tA==
46(10111000) : uA==
47(10111100) : vA==
48(11000000) : wA==
49(11000100) : xA==
50(11001000) : yA==
51(11001100) : zA==
52(11010000) : 0A==
53(11010100) : 1A==
54(11011000) : 2A==
55(11011100) : 3A==
56(11100000) : 4A==
57(11100100) : 5A==
58(11101000) : 6A==
59(11101100) : 7A==
60(11110000) : 8A==
61(11110100) : 9A==
62(11111000) : +A==
63(11111100) : /A==